
【ABC348】緑コーダーの競プロ参加記録 #11
しばらくの間、コンテスト直後にざっくりとした記事を投稿しつつ、詳細な解説をちまちま追記していくスタイルで記事を制作しようと思います。
今回はAtCoder Beginner Contest 348。使用言語はPythonです。
A問題 - Penalty Kick
コンテスト中の提出
https://atcoder.jp/contests/abc348/submissions/52060984
$${i}$$回目のチャレンジは、$${i}$$が3の倍数のとき失敗する。
$${N}$$回のチャレンジの結果を出力してね。
forループで$${1}$$から$${N}$$のすべての$${i}$$を試します。
$${i}$$が3の倍数かどうかは、$${i}$$を$${3}$$で割った余りが$${0}$$かどうかを判定します。
出力が文字列なので '+' 演算子を使って連結してもよいですが、いったんリストにまとめて join しました。
""" AC コード """
N = int(input())
ans = []
for i in range(1, N + 1):
if i % 3 == 0:
ans.append('x')
else:
ans.append('o')
print(''.join(ans))$${i}$$回目に成功するか失敗するかは$${N}$$の値に影響されないため、出力する文字列を「'oox' を無限にくり返す文字列の先頭$${N}$$文字」と捉えた解き方もできます。
""" 別解 """
N = int(input())
S = 'oox' * 100
ans = S[0:N]
print(ans)B問題 - Farthest Point
コンテスト中の提出
https://atcoder.jp/contests/abc348/submissions/52067317
$${xy}$$平面上に$${N}$$個の点がある。
それぞれの点について最も遠い点の番号を出力してね。
2点の組み合わせを全探索して、問題文に書かれている式をもとに2点間の距離$${d^2}$$を求めます。
$$
d^2 = (x_1 − x_2)^2+(y_1− y_2)^2
$$
大小比較さえできればよいので平方根 $${(\sqrt{d^2})}$$を取る必要はありません。
""" AC コード """
N = int(input())
P = [tuple(map(int, input().split())) for _ in range(N)]
for i in range(N):
res = -1
ans = 0
x1, y1 = P[i]
for j in range(N):
x2, y2 = P[j]
d = (x1 - x2) ** 2 + (y1 - y2) ** 2
if res < d:
res = d
ans = j + 1
print(ans)このようにしてもよいです。
""" 別解 """
N = int(input())
P = [tuple(map(int, input().split())) for _ in range(N)]
for x1, y1 in P:
dist = [(x1 - x2) ** 2 + (y1 - y2) ** 2 for x2, y2 in P]
ans = dist.index((max(dist))) + 1
print(ans)なお、max 関数や index メソッドはリストの長さを$${M}$$として最悪計算量が$${O(M)}$$です。
C問題 - Colorful Beans
コンテスト中の提出
https://atcoder.jp/contests/abc348/submissions/52072751
$${i}$$種類目のビーンズは美味しさ$${A_i}$$、色$${C_i}$$。
1つ色を選んで1粒食べるときの最小の美味しさの最大値を出力してね。
「最小の最大」って頭が混乱しますよね。
「同じ色の中で最も美味しくないビーンズを並べて、その中で最も美味しいやつを答えてね」という問題です。

というわけで、まず色ごとの最小値を求めます。
$${C_i \leq 10^9}$$であり list で管理できないので、dict を使います。
標準ライブラリのcollectionsモジュールから defaultdict を使うと楽です。
数値のデフォルト値は$${0}$$であり最小を求めるには不便なのでデフォルト値を大きい数に変えておきます。
""" defaultdict のデフォルト値を変更 """
from collections import defaultdict
D = defaultdict(lambda: 1 << 60)
""" 色ごとの美味しさの最小値を求める """
N = int(input())
for _ in range(N):
a, c = map(int, input().split())
D[c] = min(D[c], a)
""" 最小値の最大値を求める """
ans = max(D.values())
print(ans)D問題 - Medicines on Grid
コンテスト中の提出
https://atcoder.jp/contests/abc348/submissions/52111305
壁マスおよび薬マスを含む$${H \times W}$$のグリッドがある。
$${i}$$個目の薬を飲むとエネルギーが$${E_i}$$になる。
移動にエネルギーを$${1}$$消費する。
スタートからゴールまで移動できるか判定してね。
「あるマス$${(i, j)}$$にたどり着いたときにあり得る最大のエネルギー」を求めればいいのかなという予感からダイクストラ法が思い浮かびます。
しかし、今回の問題ではマス間を最短距離で移動する必要はなく、迂回することで最大エネルギーを更新できるかもしれません。

「$${i}$$番目の薬を飲んだとき、エネルギーが$${E_i}$$になる」というのがこの問題のカギです。
この条件により、ある薬マスから移動可能なマスは薬を飲んだ時点で確定します。
よって、到達可能な薬マスから移動可能なマスをすべて調べればよいです。
$${i}$$番目の薬マスから移動可能なマスは、その薬マスからの最短距離が$${E_i}$$以内の空きマスです。
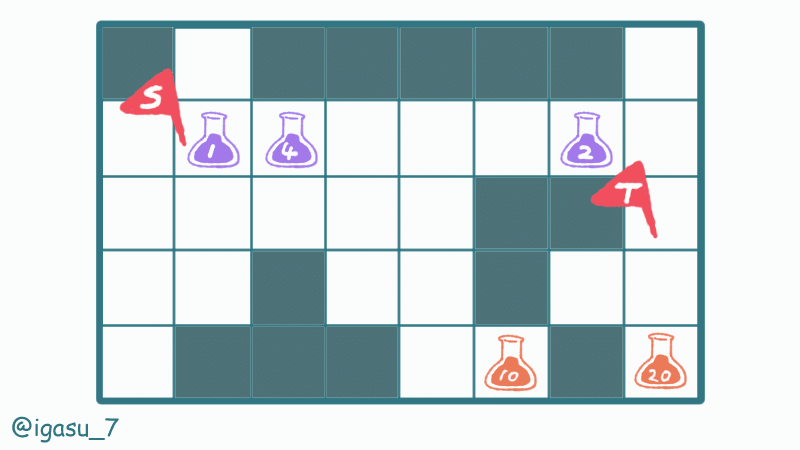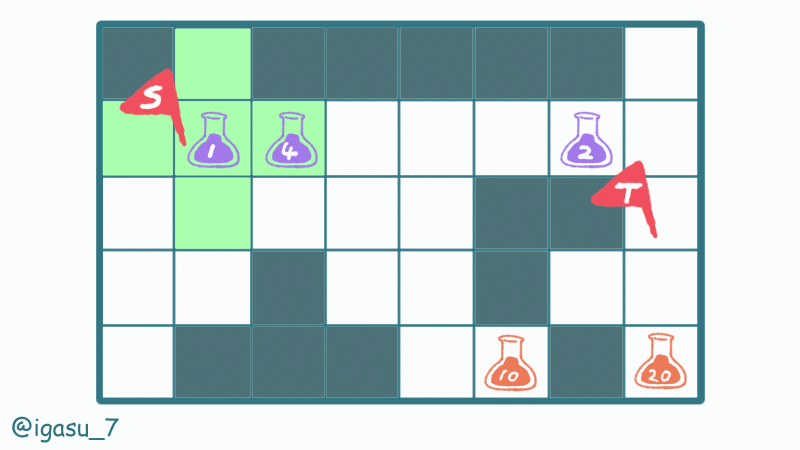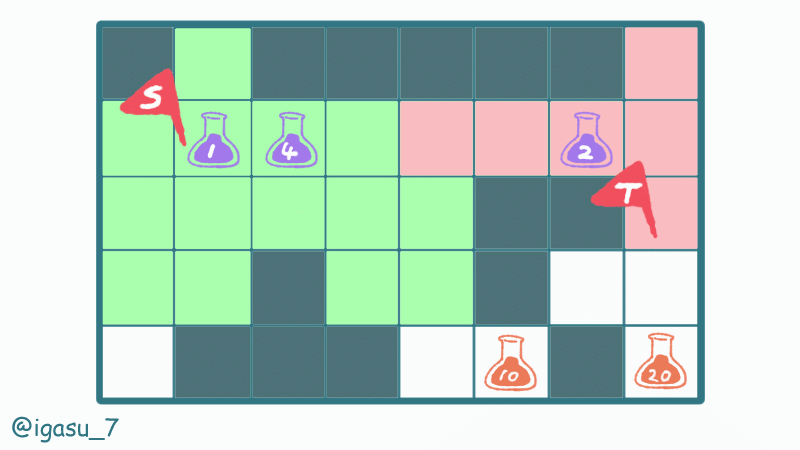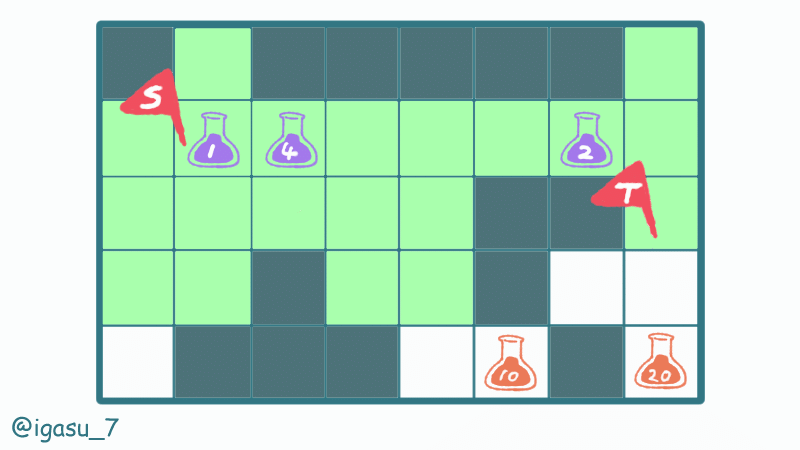
壁マスの配置によっては、薬マスからの最短距離としてマンハッタン距離を利用できないことに注意します。
それぞれの薬マスをスタート地点として移動可能なマスを BFS で全探索します。到達できない薬マスはスキップし、途中で薬を追加で飲まないものとします。
""" 全体のイメージ """
def bfs(r, c):
# 略
if is_medicine[i][j]:
medicine_pos.append((i, j))
medicine_pos = [(si, sj)]
while medicine_pos:
r, c = medicine_pos.pop()
bfs(r, c)
if reached[ti][tj]:
print('Yes')
else:
print('No')$${E \leq HW}$$より、最大$${HW}$$マスの探索を$${N}$$回行うことになるので計算量は$${HWN \leq 1.2 \times 10^7}$$程度です。
ここでは「あるマス$${(i, j)}$$が薬マスであるかどうか」「その薬のエネルギーがいくつか」をまとめて処理するために dict を使います。
""" 入力を受け取る """
from collections import deque, defaultdict
H, W = map(int, input().split())
A = [input() for _ in range(H)]
N = int(input())
medicines = defaultdict(int)
for _ in range(N):
R, C, E = map(int, input().split())
medicines[(R - 1, C - 1)] = E次に、スタートとゴールの位置を探します。
最初のエネルギーが$${0}$$なので、スタート位置が薬マスでなければその時点で答えは 'No' です。
""" スタート・ゴールの位置を探す """
start, goal = (0, 0), (0, 0)
for i in range(H):
for j in range(W):
if A[i][j] == 'S':
start = (i, j)
elif A[i][j] == 'T':
goal = (i, j)
if not start in medicines:
print('No')
exit()移動可能なマスを BFS で全探索します。
エネルギーが$${0}$$の場合は移動できないことに注意します。
""" 移動可能なマスを BFS で全探索 """
from collections import deque, defaultdict
Di = [1, -1, 0, 0]
Dj = [0, 0, 1, -1]
def bfs(r, c):
e = medicines[(r, c)]
dq = deque([(r, c, e)])
seen = [[False] * W for _ in range(H)]
seen[r][c] = True
reached[r][c] = True
while dq:
i, j, e = dq.popleft()
if e == 0:
continue
for di, dj in zip(Di, Dj):
u = i + di
v = j + dj
if not(0 <= u < H and 0 <= v < W) or seen[u][v] or A[u][v] == '#':
continue
if (u, v) in medicines and not reached[u][v]:
medicine_pos.append((u, v))
reached[u][v] = True
seen[u][v] = True
dq.append((u, v, e - 1))
reached = [[False] * W for _ in range(H)]
medicine_pos = [start]
while medicine_pos:
r, c = medicine_pos.pop()
bfs(r, c)ゴール地点に到達可能であれば答えは 'Yes' です。
""" 答えを出力 """
ti, tj = goal
if reached[ti][tj]:
print('Yes')
else:
print('No')E問題 - Minimize Sum of Distances
upsolve
https://atcoder.jp/contests/abc348/submissions/52137096
$${N}$$頂点からなる木と、数列$${C}$$が与えられる。
頂点$${a}$$と頂点$${b}$$の距離を$${d(a, b)}$$とする。
$${f(x) = \displaystyle\sum_{i=1}^N(C_i \times d(x, i))}$$の最小値を出力してね。
まず具体例で考えてみます。
次の図のような木を考えて、頂点$${1}$$を根として各頂点の深さを計算します。
そうすると、今回の問題における$${d(1, x)}$$は頂点$${x}$$の深さと一致し、$${f(1)}$$を$${O(N)}$$で求めることができます。

しかし、すべての頂点$${x}$$について同様に$${f(x)}$$を求めようとすると$${O(N^2)}$$になってしまいます。
が、いったん頂点$${1}$$の子である頂点$${5}$$について$${f(5)}$$を求めてみます。

$${f(1)}$$の例と比べて、頂点$${1, 2, 3, 4}$$の深さが +1 、頂点$${5, 6}$$の深さが -1 されています。
ここで、$${f(1), f(5)}$$を見比べてみます。

$${\displaystyle\sum_{i=5}^6C_i}$$は「頂点$${5, 6}$$の$${C}$$の総和」であり、すなわち「頂点$${5}$$を根とする部分木の$${C}$$の総和」になります。
$${\displaystyle\sum_{i=1}^4C_i}$$は「頂点$${1, 2, 3, 4}$$の$${C}$$の総和」であり、言い換えると「全体の$${C}$$の総和から、頂点$${5}$$を根とする部分木の$${C}$$の総和を引いた値」といえます。
$${f(1)}$$は最初に$${O(N)}$$で求めたので、この式に基づいてすべての$${f(x)}$$を$${O(N)}$$で求めることができそうです。
このように、部分木のもつ情報をうまく利用して、高速にすべての頂点について何かしら計算するアルゴリズムを「全方位木DP」と呼ぶそうです。
こちらの記事を参考にしました。
問題に戻ります。
まず、それぞれの「部分木の$${C}$$の総和」は任意の頂点を根として DFS で求めることができます。
頂点$${x}$$を根とする「部分木の$${C}$$の総和」を$${sub[x]}$$とします。
""" 入力を受け取る """
N = int(input())
G = [[] for _ in range(N + 1)]
for _ in range(N - 1):
a, b = map(int, input().split())
G[a - 1].append(b - 1)
G[b - 1].append(a - 1)
C = list(map(int, input().split()))def pre_dfs(curr, prev, depth):
""" 部分木の C_i の総和を求める。(ついでにf(0)も求める。) """
global f0
f0 += C[curr] * depth
sub[curr] += C[curr]
for nxt in G[curr]:
if nxt == prev:
continue
sub[curr] += pre_dfs(nxt, curr, depth + 1)
return sub[curr]
""" f(x) の計算に使うコストの差分を求める """
f0 = 0
sub = [0] * N
pre_dfs(0, -1, 0)次に、ある頂点$${x}$$について$${f(x)}$$が求まっている状態から、その子である頂点$${y}$$について$${f(y)}$$を求めたいです。
上のコードでは頂点$${0}$$を木全体の根にしたので$${\mathrm{sum}(C) = sub[0]}$$であり、以下が成り立ちます。
$$
f(y) = f(x) - sub[y] + (sub[0] - sub[y])
$$
これを利用してすべての$${f(x)}$$を DFS 順に求めることができます。
その中の最小値を答えとして出力します。
def solve_dfs(curr, prev, f_curr):
""" f(nxt) を f(curr) との差分から求める """
global ans
ans = min(ans, f_curr)
for nxt in G[curr]:
if nxt == prev:
continue
f_nxt = f_curr - sub[nxt] + (sub[0] - sub[nxt])
solve_dfs(nxt, curr, f_nxt)
""" すべての f(x) を求める """
ans = f0
solve_dfs(0, -1, f0)
print(ans)全体の計算量は$${O(N)}$$です。
あとがき
今回はABCD 4完 104分で 2802位、1033 perf でした。
D問題に90分使いましたが、解けたのでよしとします。
ではまた~。

【更新履歴】
2024/04/07 (1時頃): 記事投稿。
2024/04/07 (19時頃): E問題の解説を追加。
2024/04/08 (20時頃): 文章を追加。完成!
