
【ABC351】緑コーダーの競プロ参加記録 #15
今回はAtCoder Beginner Contest 351。使用言語はPythonです。
A問題 - The bottom of the ninth
コンテスト中の提出
https://atcoder.jp/contests/abc351/submissions/52835028
チーム$${A}$$とチーム$${B}$$が野球をしており、現在9回裏。
チーム$${A, B}$$の$${i}$$回の攻撃の得点状況はそれぞれ$${A_i, B_i}$$
チーム$${B}$$が勝つためにあと何点必要か出力してね。
現在のチーム$${A, B}$$の得点はそれぞれ$${\mathrm{sum}(A), \mathrm{sum}(B)}$$です。
制約から、$${\mathrm{sum}(A) \geq \mathrm{sum}(B)}$$であることが保証されています。
チーム$${B}$$は$${\mathrm{sum}(A) - \mathrm{sum}(B)}$$点を取ることで同点にすることができます。
よって、さらに +1 点取ることで勝つことができます。
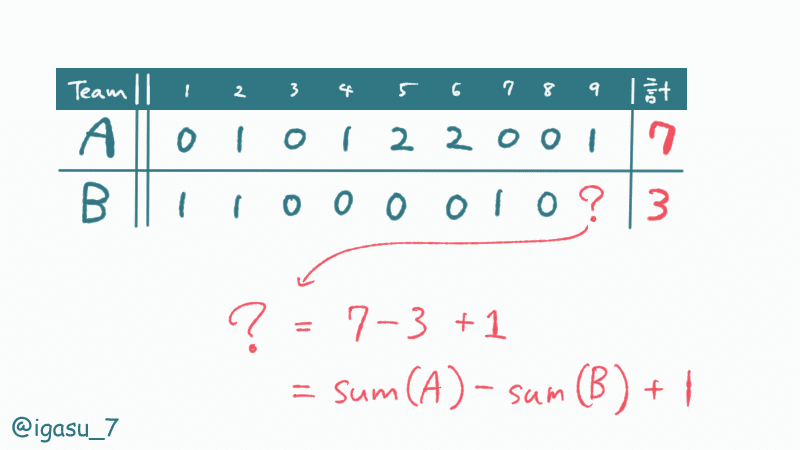
""" AC コード """
A = list(map(int, input().split()))
B = list(map(int, input().split()))
ans = sum(A) - sum(B) + 1
print(ans)B問題 - Spot the Difference
コンテスト中の提出
https://atcoder.jp/contests/abc351/submissions/52838390
$${N \times N}$$のグリッド$${A, B}$$が与えられる。
$${A, B}$$の1マスだけ文字の異なるマス$${(i, j)}$$を出力してね。
2つのグリッドを全探索すればよいです。
全探索するときは 0-index ですが、出力は 1-index になることに注意してください。
""" AC コード """
N = int(input())
A = [input() for _ in range(N)]
B = [input() for _ in range(N)]
for i in range(N):
for j in range(N):
if A[i][j] != B[i][j]:
print(i + 1, j + 1)
exit()C問題 - Merge the balls
コンテスト中の提出
https://atcoder.jp/contests/abc351/submissions/52854398
空の列と$${N}$$個のボールがある。
$${i}$$番目のボールの大きさは$${2^{A_i}}$$。
$${N}$$回の操作後の列のボールの数を出力してね。
操作 1: $${i}$$番目のボールを列の右に追加する。
操作 2: 列の右側2つのボールの大きさが等しい限り、2つのボールを取り除き、大きさが「2つのボールの和」であるボールを列の右に追加する。
$${0 \leq A_i \leq 10^9}$$なので、ボールの大きさ$${2^{A_i}}$$をそのまま表現することができません。
(基本的にはPythonでオーバーフローすることはありませんが、大きすぎる数の計算はとても時間がかかります。)
列の右側2つのボールの大きさが異なる場合は、ただ追加するだけなので素直にシミュレーションしてよく、トータルの計算量は$${O(N)}$$です。
列の右側2つのボールの大きさが等しい場合は、2つのボールの大きさを足し合わせます。
しかし前述の通り、ボールの大きさはそのまま表現できません。
ここで、「ある2つの等しい数を足す」ことと「ある数を2倍する」ことは同じであることに着目します。
また、$${2^k}$$を$${2}$$倍すると$${2^{k + 1}}$$になります。
よって、ボールの大きさは$${A_i}$$として表現し、操作 2 では$${A_i + 1}$$とすればよいです。
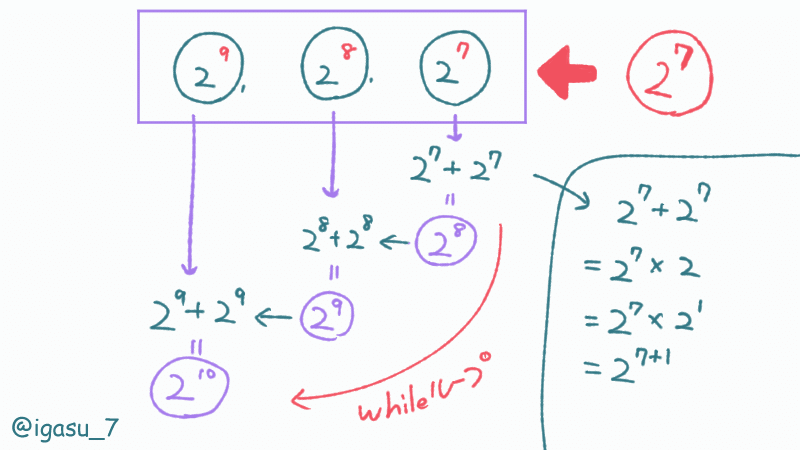
「2つのボールを1つのボールに変換する処理」は「ボールを1つ減らす処理」とみなすことができ、最大で$${N}$$回行われるので、トータルの計算量は$${O(N)}$$です。
(追加した分しか減らせないという考え方です。)
""" AC コード """
N = int(input())
A = list(map(int, input().split()))
B = []
for i in range(N):
B.append(A[i])
while len(B) > 1 and B[-1] == B[-2]:
x = B.pop()
B.pop()
B.append(x + 1)
print(len(B))D問題 - Grid and Magnet
コンテスト中の提出
https://atcoder.jp/contests/abc351/submissions/52875500
$${H \times W}$$のグリッドが与えられる。
'.' マスは空きマス、 '#' マスは磁石マス。
磁石マスの上下左右にいる場合、移動不可。
あるマスからスタートして移動可能なマスの個数の最大値を出力してね。
次のようなマスを考えてみます。

'#' マスの上下左右はそこから移動不可になるマスです。'o’ マークをつけてみます。

移動不可の 'o' マークを避けて移動すれば、どこへでも自由に移動できます。
たとえば、マス$${(1, 1)}$$からスタートして自由に移動できるマスを紫色で塗ってみます。

紫マスの中であれば、どこのマスからスタートしても同じです。
紫マスの個数を数え上げる問題であれば「'o' マスと '#' マスを壁マスとみなしたBFS」で解くことができます。
実際には 'o' マスに到達することも可能なので、到達可能な 'o' マスもカウントに含めます。
通常、グリッドをBFSする問題では探索済みマスを管理するリストを用意しますが、今回の問題では不用意に 'o' マスを探索済みにすると WA になるケースがあります。
たとえば、以下のようなグリッドにおいてスタート位置を左上から全探索する場合、$${(1, 1)}$$からスタートした時にオレンジ色のマス$${(2, 3), (3, 3), (5, 3)}$$を先に探索済みとしてしまうと、$${(1, 5)}$$からスタートした時に探索するマスがその分減ってしまう可能性があります。

まず、磁石マスおよびその上下左右をゴール地点とみなして、ゴール位置を先に調べておきます。
""" 磁石マスとその上下左右のマスの位置を特定する """
H, W = map(int, input().split())
S = [input() for _ in range(H)]
is_goal = [[False] * W for _ in range(H)]
Di = [0, 0, 1, -1]
Dj = [1, -1, 0, 0]
for i in range(H):
for j in range(W):
if is_goal[i][j] or S[i][j] == '.':
continue
is_goal[i][j] = True
for di, dj in zip(Di, Dj):
u = i + di
v = j + dj
if not(0 <= u < H and 0 <= v < W) or S[u][v] == '#':
continue
is_goal[u][v] = Trueスタート地点を全探索し、未探索マスであればそこから BFS を行います。
""" 未探索のマスをスタート地点として BFS をする """
ans = 1
for i in range(H):
for j in range(W):
if seen[i][j] or is_goal[i][j]:
continue
ans = max(ans, bfs(i, j))
print(ans)前述の通り、ゴールマスについては探索済みフラグの管理に注意が必要です。また、ゴールマスからは次のマスに移動できません。
""" BFS で移動可能なマスの個数を数える """
from collections import deque
Di = [0, 0, 1, -1]
Dj = [1, -1, 0, 0]
seen = [[False] * W for _ in range(H)]
def bfs(si, sj):
dq = deque([(si, sj)])
res = 0
seen_goal = set() # 探索済みのゴールマスを別で管理する
while dq:
i, j = dq.popleft()
if seen[i][j] or (i, j) in seen_goal:
continue
res += 1
if is_goal[i][j]:
seen_goal.add((i, j))
continue
seen[i][j] = True
for di, dj in zip(Di, Dj):
u = i + di
v = j + dj
if not(0 <= u < H and 0 <= v < W) or S[u][v] == '#' or seen[u][v]:
continue
dq.append((u, v))
return resなお、上記コード中の$${Di, Dj}$$については以下の図のイメージです。

E問題 - Jump Distance Sum
upsolve
https://atcoder.jp/contests/abc351/submissions/52938495
座標平面上に$${N}$$個の点がある。
斜め移動での点$${P_i, P_j}$$の最短距離が$${\mathrm{dist}(P_i, P_j)}$$。
$${\displaystyle\sum_{i = 1}^{N-1} \displaystyle\sum_{j = i+1}^{N} \mathrm{dist}(P_i, P_j)}$$を出力してね。
点を原点を中心に$${45}$$度回転し、 $${\sqrt2}$$倍に拡大することを考えます。このとき、元々$${(X,Y)}$$にあった点は$${(X+Y,X−Y)}$$に移動します。
公式解説がこの一文から始まっています。
斜め移動どうする?
まず、斜めに移動するとはどういうことか見てみます。

斜めに1回ジャンプすることは、45度方向に長さ$${\sqrt2}$$進むことと同じです。
ここで45度回転をすると、移動を「斜め」から「上下左右」に変換できます。
本来、点$${(x, y)}$$の$${\theta}$$回転を表す式は以下の通りです。
$$
\begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{pmatrix}
\begin{pmatrix}
x \\ y
\end{pmatrix}
=
\begin{pmatrix}
x\cos\theta - y\sin\theta \\
x\sin\theta + y\cos\theta
\end{pmatrix}
$$
上式をもとに$${\theta = 45\degree}$$とすると、点$${(x, y)}$$は$${(\frac{1}{\sqrt2}(x - y), \frac{1}{\sqrt2}(x + y))}$$に移動します。
座標に$${\frac{1}{\sqrt2}}$$が含まれているのは(競プロ上?)都合が悪いので、これを$${\sqrt2}$$倍して整数のまま扱えるようにします。
これが「45度回転して$${\sqrt2}$$倍」というテクニックの正体です。
この操作によって点$${(x, y)}$$は$${(x - y , x + y)}$$に移動します。
元々、1回のジャンプは「斜めに$${\sqrt2}$$進む」ことだったので、「45度回転して$${\sqrt2}$$倍」することによって「上下左右に$${2}$$進む」ことに変わります。
なお、$${\theta = -45\degree}$$として点$${(x, y)}$$を$${(x + y , x - y)}$$としても同様に解くことができます。
(回転行列では反時計回りを正としています。)
本記事では、公式解説に合わせて$${\theta = -45\degree}$$としています。
点Aから点Bに移動できる?
次に、2点$${A, B}$$間で移動可能かどうか考えます。
移動できなければ$${\mathrm{dist}(A, B) = 0}$$です。
座標を回転せず考えると、1回の斜め移動では$${x, y}$$ともに$${+1}$$または$${-1}$$だけ変化しますが、移動前後で$${x + y}$$の偶奇が変わりません。
よって、点$${(x, y)}$$について$${x + y}$$の偶奇でグループ分けができます。
「45度回転して$${\sqrt2}$$倍」してから考えると、1回の移動で$${x, y}$$のどちらかが$${+2}$$または$${-2}$$だけ変化しますが、移動前後で$${x,y}$$それぞれの偶奇は変わりません。
回転前の$${x, y}$$それぞれの偶奇の組み合わせについて$${x + y, x - y}$$それぞれの偶奇を考えてみると以下の図のようになります。
よって、回転後の点$${(x, y)}$$について「$${x, y}$$ともに偶数」「$${x, y}$$ともに奇数」のグループに分けられます。

グループ分けは、どちらの方法を選んでもよいです。
グループの異なる2点の間を移動することは出来ません。
問題を解く
さて、与えられたすべての点を「45度回転して$${\sqrt2}$$倍」して考えます。
""" 移動可能な点同士をグループ分けして 45度回転 & √2倍 """
N = int(input())
even, odd = [],[]
for _ in range(N):
x, y = map(int, input().split())
if (x + y) % 2 == 0:
even.append((x + y, x - y))
else:
odd.append((x + y, x - y))先に述べたように、変換後のジャンプは「上下左右に$${2}$$進む」ことに変わります。
つまり、「1回のジャンプ」と「マンハッタン距離$${2}$$」が同じ意味になります。
重要な性質として、マンハッタン距離を考えるときは$${x}$$座標と$${y}$$座標を分けて考えることができます。
これは、2点$${(x_1, y_1), (x_2, y_2)}$$のマンハッタン距離が$${|x_1 - x_2| + |y_1 - y_2|}$$であることから明らかです。
以下では、$${x}$$座標だけに着目してみます。
同一グループ内の点の個数を$${E}$$とします。
$${E}$$個の点から2点間の距離をすべて求めようとすると$${O(E^2)}$$になってしまうので、どうにかして計算量を落としたいです。
具体的に、$${E = 4}$$の点を並べて$${|x_j - x_i|}$$を見てみます。
それぞれの点の$${x}$$座標を$${[1, 5, 7, 11]}$$とします。

図を見ると、$${i < j, x_i \leq x_j}$$が満たされていれば、$${i}$$を固定したとき$${E - i}$$個の$${x_j}$$の総和から$${E - i}$$個分の$${x_i}$$を引くことで$${\displaystyle\sum_{j = i + 1}^E|x_j-x_i|}$$を$${O(1)}$$で求めることができそうです。
よって、グループ内の点をソートして、累積和をとり、$${i}$$を全探索することで$${O(E)}$$ですべての$${\mathrm{dist}}$$を計算できます。
これを、$${x}$$座標ごと、$${y}$$座標ごと、各グループごとに計算します。
""" グループごとに dist をすべて計算する """
from itertools import accumulate
def solve(P):
E = len(P)
X = sorted([x for x, _ in P])
Y = sorted([y for _, y in P])
acc_x = list(accumulate(X))
acc_y = list(accumulate(Y))
res = 0
for i in range(E):
res += acc_x[E - 1] - acc_x[i] - X[i] * (E - i - 1)
res += acc_y[E - 1] - acc_y[i] - Y[i] * (E - i - 1)
return resいま、「1回のジャンプ」と「マンハッタン距離$${2}$$」が同じ意味になっているので、計算結果を$${2}$$で割ることで元の問題の答えが得られます。
""" 2 で割った答えを出力 """
ans = solve(even) + solve(odd)
ans //= 2
print(ans)「45度回転して$${\sqrt2}$$倍」というテクニックに関して、「競プロ典型90問」に同様の問題があります。
F問題 - Double Sum
upsolve
https://atcoder.jp/contests/abc351/submissions/52958319
長さ$${N}$$の整数列$${A}$$が与えられる。
$${\displaystyle\sum_{i = 1}^{N} \displaystyle\sum_{j = i+1}^{N} \mathrm{max}(A_j-A_i, 0)}$$を出力してね。
E問題でも似たような式が出てきました。
E問題と同様に$${i< j , A_i < A_j}$$を満たすグループ内で$${A_j}$$の総和と個数を調べ、その個数分の$${A_i}$$を引くことで$${\displaystyle\sum_{j = i + 1}^N A_j - A_i}$$を高速に計算できます。
E問題と異なるのは、グループ内の値でソートできない点です。
絶対値をとらないため$${A_i, A_j}$$の大小関係によって引き算の結果が変わってしまうからです。
ある値$${x}$$の個数を$${O(1)}$$で参照したいとき、$${\mathrm{cnt}[x]}$$のようなリストを前計算して用意すると思います。
$${x < y}$$を満たす$${\mathrm{cnt}[y]}$$の総和を求めたいときは、区間和として累積和の差から計算します。
今回の問題では、$${i}$$を1つずつ進めながら上記のような累積和を更新しつつ、そのときの区間和を計算する問題です。
これはセグ木を使うことで高速に行うことができます。
""" セグ木 """
class SegTree:
def __init__(self, m):
self.n = 1 << (m - 1).bit_length()
self.node = [0] * (2 * self.n)
def add(self, a, x):
a += self.n
self.node[a] += x
while a > 0:
a >>= 1
self.node[a] = self.node[2 * a] + self.node[2 * a + 1]
def query(self, a, b):
a += self.n
b += self.n
res = 0
while a < b:
if a & 1 == 1:
res += self.node[a]
a += 1
if b & 1 == 1:
res += self.node[b - 1]
a >>= 1
b >>= 1
return res$${A_i \leq 10^8}$$より、長さ$${\mathrm{max}(A_i)}$$のリストをセグ木で管理すると MLE やら TLE になりそうです。
$${A_i \leq A_j}$$を満たす範囲が知りたい、すなわち大小関係が保たれていればよいので、座標圧縮をします。
""" 座標圧縮をする """
from collections import defaultdict
N = int(input())
A = list(map(int, input().split()))
D = defaultdict(int)
for i, a in enumerate(sorted(set(A))):
D[a] = i
M = len(D)あとは$${A_i}$$の値とその個数について2つのセグ木を用意し、$${i}$$を1つずつ進めながらセグ木を更新していけばよいです。
$${A}$$を逆順に見ていくと楽です。
""" A の逆順にセグ木を更新しながら答えを計算 """
seg_cnt = SegTree(M)
seg_num = SegTree(M)
ans = 0
for a in reversed(A):
i = D[a]
num = seg_num.query(i, M)
cnt = seg_cnt.query(i, M)
ans += num - a * cnt
seg_num.add(i, a)
seg_cnt.add(i, 1)
print(ans)この解法は、数列の転倒数を求める方法と似ています。
転倒数を求めるアルゴリズムとしてFenwick Tree、Binary Indexed Tree と呼ばれるデータ構造を使うものが有名です。
これはセグ木の機能縮小版みたいなもので、セグ木より高速に動きます。
""" FenwickTree (Binary Indexed Tree) """
class FenwickTree:
def __init__(self, n):
self.n = n
self.node = [0] * self.n
def add(self, a, x):
a += 1
while a <= self.n:
self.node[a - 1] += x
a += a & -a
def query(self, a, b):
""" [a, b) の区間和 """
return self._query(b) - self._query(a)
def _query(self, a):
""" [0, a) の区間和 """
res = 0
while a > 0:
res += self.node[a - 1]
a -= a & -a
return resFenwick Treeの実装についてはこちらの記事が分かりやすかったのでご紹介します。
あとがき
今回はABCD 4完 69分 (1ペナ) で 2620位、1098 perf でした。
今月はABCで5完ができませんでした。
毎回水 diff の問題があったのでどれか1つは解きたかったところ。
来月も頑張っていきましょう。
マイペースで。
ではまた~。



【更新履歴】
2024/04/28 (1時頃):記事投稿。
2024/04/29 (21時頃):E問題を追加。
2024/04/30 (16時頃):F問題を追加。
