pythonのmatplotlibでsin 3θとcos 3θのグラフを作成する

$${\sin3\theta}$$(3倍角)のグラフを描いてみます。単純にグラフを作成すると、$${\sin\theta}$$に比べて周波数が3倍になることがわかります。

import numpy as np
import matplotlib.pyplot as plt
N = 100
t = np.linspace(-1, 1, N)
omega_1 = 2 * np.pi * 1
omega_3 = 2 * np.pi * 3
sin_1 = np.sin(t * omega_1)
sin_3 = np.sin(t * omega_3)
fig ,ax = plt.subplots()
plt.rcParams["figure.figsize"] = (6, 4)
ax.set_title( r'$ f=1:\omega=2\pi$と$ f=3:\omega=6\pi$のグラフ', loc = 'center', pad=30, fontname="MS Gothic", fontsize = 24)
ax.plot(t, sin_1, color='g', label= r'$f=1:\omega=2\pi$')
ax.plot(t, sin_3, color='r', label= r'$f=3:\omega=6\pi$')

ax.set_xlabel('t', loc = 'right', labelpad=-30)
ax.set_yticks([-1, -1/2**0.5, -0.5, 0,0.5, 1/2**0.5,1]) 
ax.set_yticklabels( [ '-1', r'$-\frac{1}{\sqrt{2}}$',r'$-\frac{1}{2}$', '0',r'$\frac{1}{2}$',r'$\frac{1}{\sqrt{2}}$','1'])
ax.spines['left'].set_position('zero') 
ax.spines['bottom'].set_position(('data', 0))
ax.spines["right"].set_color("none")
ax.spines["top"].set_color("none")
ax.legend( bbox_to_anchor=(1, 0.2))
ax.set_aspect(0.5, adjustable='box')
ax.grid(which = "major", axis = "x", color = "green", alpha = 0.8,
        linestyle = "--", linewidth = 0.5)
ax.grid(which = "major", axis = "y", color = "green", alpha = 0.8,
        linestyle = "--", linewidth = 0.5)
plt.show()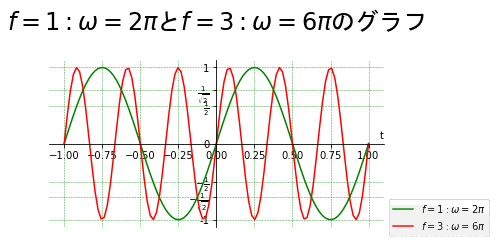

 ところで$${\sin\theta=3\sin\theta-4\sin^3\theta}$$の公式を使い同じ曲線を描いてみます。

import numpy as np
import matplotlib.pyplot as plt
N = 100
theta = np.linspace(-2*np.pi, 2*np.pi, N)
sin_ = np.sin(theta)
sin_3 = np.sin(3*theta)
tri_ = 3 * sin_ - 4*  sin_ **3
fig ,ax = plt.subplots()
plt.rcParams["figure.figsize"] = (6, 4)
ax.set_title( r'$\sin 3 \theta$と$3 \sin \theta - 4\sin^3 \theta$の関係', loc = 'center', pad=30, fontname="MS Gothic", fontsize = 24)
ax.plot(theta, sin_, color='g', linewidth=1, label= r'$\sin \theta$')
ax.plot(theta, sin_3, color='g', linewidth=8, alpha = 0.2, label= r'$\sin 3\theta$')
ax.plot(theta, tri_, color='r', linewidth=1,label= r'$3 \sin \theta - 4\sin^3 \theta$')
ax.set_xticks([-2*np.pi,-1.5*np.pi, -np.pi,-0.5*np.pi,0,0.5*np.pi, np.pi,1.5*np.pi, 2*np.pi]) 
ax.set_xticklabels( [ '-2π',r'$-\frac{3}{2} \pi$' ,'-π', r'$-\frac{π}{2} \pi$','', 
         r'$\frac{π}{2} \pi$','π', r'$\frac{3}{2} \pi$', '2π'])
ax.set_xlabel(r'$\theta$', loc = 'right', labelpad=-30)
ax.set_yticks([-1, -1/2**0.5, -0.5, 0,0.5, 1/2**0.5,1]) 
ax.set_yticklabels( [ '-1', r'$-\frac{1}{\sqrt{2}}$',r'$-\frac{1}{2}$', '0',r'$\frac{1}{2}$',r'$\frac{1}{\sqrt{2}}$','1'])
ax.spines['left'].set_position('zero') 
ax.spines['bottom'].set_position(('data', 0))
ax.spines["right"].set_color("none")
ax.spines["top"].set_color("none")
ax.legend( bbox_to_anchor=(1, 0.2))
# ax.set_aspect(2, adjustable='box')
ax.grid(which = "major", axis = "x", color = "green", alpha = 0.8,
        linestyle = "--", linewidth = 0.5)
ax.grid(which = "major", axis = "y", color = "green", alpha = 0.8,
        linestyle = "--", linewidth = 0.5)
plt.show()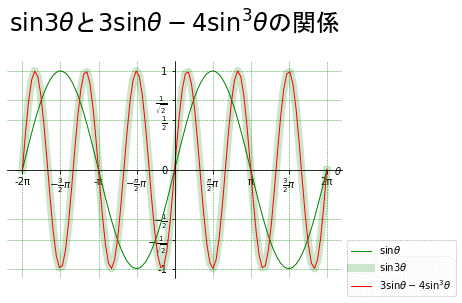

同じように$${\cos 3\theta}$$についてもグラフを作成します。

import numpy as np
import matplotlib.pyplot as plt
N = 100
theta = np.linspace(-2*np.pi, 2*np.pi, N)
cos_ = np.cos(theta)
cos_3 = np.cos(3*theta)
tri_ =  4*cos_ **3 - 3 * cos_
fig ,ax = plt.subplots()
plt.rcParams["figure.figsize"] = (6, 4)
ax.set_title( r'$\cos 3 \theta$と$4\cos^3 \theta -3 \cos \theta$の関係', loc = 'center', pad=30, fontname="MS Gothic", fontsize = 24)
ax.plot(theta, cos_, color='g', linewidth=1, label= r'$\cos \theta$')
ax.plot(theta, cos_3, color='g', linewidth=8, alpha = 0.2, label= r'$\cos 3\theta$')
ax.plot(theta, tri_, color='r', linewidth=1,label= r'$4\cos^3 \theta - 3 \cos \theta$')
ax.set_xticks([-2*np.pi,-1.5*np.pi, -np.pi,-0.5*np.pi,0,0.5*np.pi, np.pi,1.5*np.pi, 2*np.pi]) 
ax.set_xticklabels( [ '-2π',r'$-\frac{3}{2} \pi$' ,'-π', r'$-\frac{π}{2} \pi$','', 
         r'$\frac{π}{2} \pi$','π', r'$\frac{3}{2} \pi$', '2π'])
ax.set_xlabel(r'$\theta$', loc = 'right', labelpad=-30)
ax.set_yticks([-1, -1/2**0.5, -0.5, 0,0.5, 1/2**0.5,1]) 
ax.set_yticklabels( [ '-1', r'$-\frac{1}{\sqrt{2}}$',r'$-\frac{1}{2}$', '0',r'$\frac{1}{2}$',r'$\frac{1}{\sqrt{2}}$','1'])
ax.spines['left'].set_position('zero') 
ax.spines['bottom'].set_position(('data', 0))
ax.spines["right"].set_color("none")
ax.spines["top"].set_color("none")
ax.legend( bbox_to_anchor=(1, 0.2))
# ax.set_aspect(2, adjustable='box')
ax.grid(which = "major", axis = "x", color = "green", alpha = 0.8,
        linestyle = "--", linewidth = 0.5)
ax.grid(which = "major", axis = "y", color = "green", alpha = 0.8,
        linestyle = "--", linewidth = 0.5)
plt.show()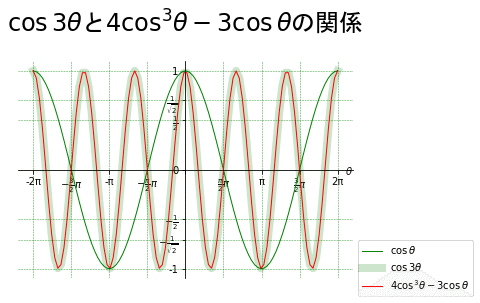

$${\cos 3\theta=4\cos^3 \theta - 3 \cos \theta}$$の公式の結果と一致します。