日本の新型コロナウイルス感染状況の考察

Ⅰ はじめに Ⅱ 理論 1最適化適合関数２感染症の各症状の推移
Ⅲ最適化関数適合 １前提条件
Ⅳガウス関数の最適化適合１標準偏差平均値の設定 ２死亡者推移の最適化適合 ３総感染者推移の最適化適合 ４市中感染者予測 Ⅴ感染から発症,検査 Ⅵ結論 Ⅶおわりに 参考文献

Ⅰ．はじめに
　中国の湖北省武漢市で発生した新型コロナウィルス（ＣＯＶＩＤ‐19）は、２０２０年現在も世界的に感染拡大している。世界保健機構（ＷＨＯ）がパンデミック（世界的大流行）を宣言した。日本でも１月に感染者が確認され、更にクルーズ船の寄港により新型コロナウィルスの危機感が高まった。２月中旬から全国の主要都市で発症者が確認され。感染拡大となった。放射線計測の情報処理の経験から感染予測が可能ではと考え、各自治体の公表するＣＯⅤⅠＤ-19のデータの収集を始め、数理解析を３月末から開始した。感染症で一番に重要な情報は市中に感染を広めるスプレッダーとスーパースプレッダーの存在である。これらの分布を推測するモデルを考察する。
　本論では、北海道,東京都,神奈川県,埼玉県,千葉県,愛知県,大阪府,兵庫県,福岡県の９都道府県の公表データの解析を進めているが、代表例として大阪府と埼玉県について考察する。初期の頃は、感染症の専門家の発言した①ＰＣＲ検査基準（発熱３７．５℃以上が四日間続く患者が検査対象）、②陽性者の分布は２週間前の状態、③感染者は１０万～２０万になる、などデータに基づかない発言国民の不安が高まった。これら発言内容の検証と市中感染者数の予測モデルを考察する。なお、市中感染者の時間推移データを基に推測した事例はないので、本論で予測した。

Ⅱ．理　論
１． 最適化適合関数
　ウィルスに関する文献を調査すると実効再生産数の理論など放射線計測の散乱吸収の理論の応用であることから、感染者の推移も放射線計測で適用していた自然関数が適合可能であると考え、感染予測モデルとして適用した。
適用した最適化関数は以下のガウス関数である。
F＝１/（√（２π）×σ）×exp｛－１×（ｔ－μ）**２｝×α + 指数関数
　　　　但し、σ：標準偏差　μ：平均値　ｔ：時間　α：ピーク値
　ガウス関数やポアソン分布関数は、放射線計測において４０年前（１９７０年代）に適用していた最適化関数である。なお、放射線と同様に感染推移も収束時に余波的に傾斜が鈍化する傾向を想定し、補填するために指数関数を付加した。
　新規のクラスター等の発生については、その都度最適化関数を合成することで対応可能である。

２． 感染症の各症状の推移
感染症の各症状（無症状、軽症、中等症状、重症、死亡）の時間推移はガウス分布となり、図に示す積分曲線となる。
更に、市中感染者数は以下の計算式で推測する。
（１）市中感染者数＝感染者数―確定感染者数―市中感染者回復者数
（２）感染者数 ≒死亡者数÷死亡率
　　　　　　　≒重症者数÷重症率
　　　　　　　≒中等症者数÷中等症率
　　　　　　　≒確定陽性者数÷検査率
　以上の計算式を踏まえ、新型コロナウィルスの感染者の推移モデルを下記に示す

Ⅲ．最適化関数適合
　　　最適化関数適合については、通常は複合サーバ群やスーパーコンピュータを使用して最小２乗法やχ２乗法で解析を行う必要がある。４０年前は汎用機を利用して最適化解析を行っていた。本論では、既に退官した身分のため、処理速度の速い計算機を使用することができないためパソコンのＥｘｃｅｌで簡易解析を行った。
Ⅲ－１　前提条件
１． 論文等から死亡率を０．８％～１．０％とした。本論で前提とした条件は死亡率のみである。
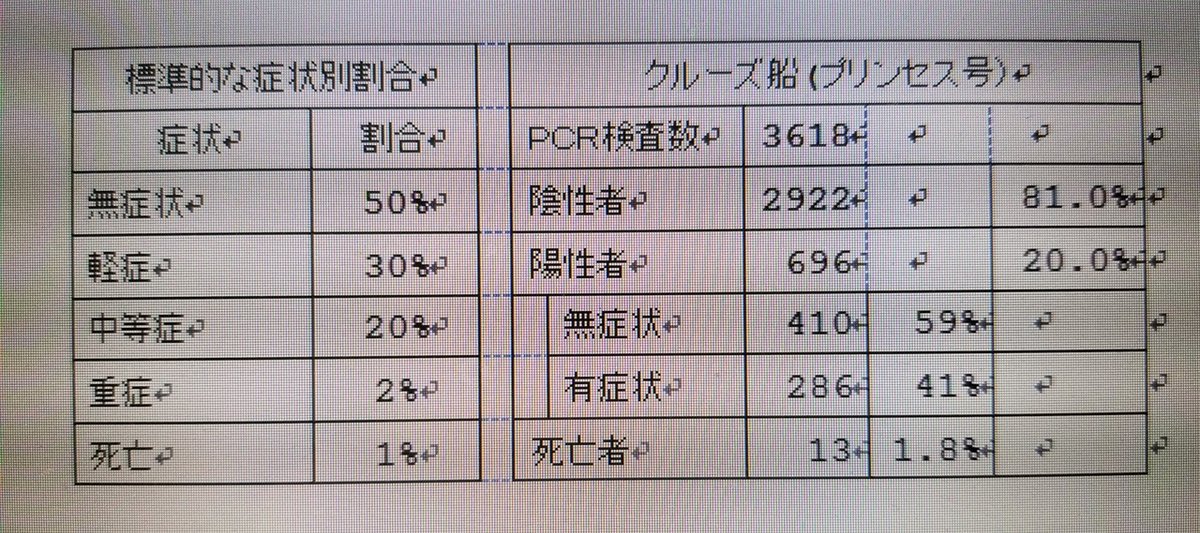
一般的に公開されている症状別の割合は下表である。また、参考までに２月に寄港したクルーズ船（プリンセス号）は環境的には高齢者率が高く、閉鎖環境であったが、下記に参考値として示した。高齢者率が高い（１．８％）クルーズ船を踏まえると死亡率０．８％～１．０％は妥当と推察する。

２． データの平均化
　放射線計測などにおいては平均化を３点平均で行うことが一般的であるが、ＰＣＲ検査機関等の曜日による実施体制を考慮して土日曜日の件数減、また患者も症状次第により検査日が前後することを考えデータは前後３日間の７日平均値を採用して平均化を行うこととした。

Ⅲ－２ガウス関数の最適化適合
１． 標準偏差、平均値の設定
陽性者数の微分値曲線から標準偏差σと平均値μの初期値を算定する。標準偏差σは＋ピーク地点とゼロ点交差点との間隔である。また、平均値μはゼロ交差点である。なお、最高点から最下点が半値幅FWHM＝２．３５σである。この微分値による数値処理は４０年前から放射線計測のスペクトル解析時にピーク位置の推定法としてよく使われてきた手法である。

　感染状況の推移の指標方法としては、実効再生産数もあるが、簡単に計算できる検査陽性者数の平方根√値の推移による監視も有効である。
平方根√値は数値誤差（数値のバラツキ）の平滑化ができ、的確は推移把握が可能である。この√値は、４０年前から自然対数表示（Ｌog10)とともに、放射線計測において測定値の有効性の検証方法として誤差（√測定値）の数値処理や表示によく使われる手法である。

２． 死亡者推移の最適化適合
死亡率を１．０％とし、総感染者数推移を死亡者数推移（積分値及び日別死亡者数）から換算する。更に、最適化死亡者関数（ガウス関数）を最小２乗法またはχ２乗法により関数適合を行う。
最適化積分関数と陽性者累計から検査率を設定する。
　　　　検査率＝陽性者数÷総感染者数
複数のクラスターによる合成の場合は、主たる分布により検査率の設定を行うこととした。

３． 総感染者推移の最適化適合
　検査率からの推定感染者数の推移を予測し、標準偏差σと平均値μの初期値を前提に積分値及び日別感染者推移と最適化感染関数を最小２乗法またはχ２乗法により関数適合を行う。
なお、下記大阪の推移図では、重傷者数による最適化が可能であるため、参考として表示した。
　死亡者数以外にも必ず入院が必要な中等症患者数や重傷者数からも推定が可能であるが、データが公表されていないため、本論では採用出来なかった。

４． 市中感染者予測
　総感染者推移から市中感染者の推定を行った。大阪府と埼玉県の新型コロナウィルス感染状況を以下の図に示した。総感染者数及び市中感染者数は以下の図から数値が推測できる。
なお、市中感染者数の計算式を示す。
　　市中感染者数＝総感染者数－確定陽性者数－市中感染回復者数
　大阪府の感染状況の最適化関数の適合結果図に陽性者数の推移を表示した。さらに陽性者の回復数についても回復推移曲線と実際の回復者の推移が非常に合っていることからも本理論の信頼性が高いと考察する。
　調査分析を行った９都道府県の推定した総感染者数と市中感染者数を表に示した。表から東京都は人口比０．３％の感染、他の道府県は０．１％となった。なお、愛知県と福岡県は感染の大部分がクラスター感染であったため人口比が低い数値となったと思われる。

　埼玉県の回復数の推移は本論の推定と合っていないが、他の都道府県の適合を考慮すると、埼玉県の退院基準が違う可能性が高いと思われる。なお、解析した都道府県のうち千葉県と埼玉県以外は非常に適合している。

Ⅳ．感染から発症,検査
　埼玉県と神奈川県が公表している感染者情報を基に発症日及び検査及び陽性確定日の日数を分析した。
　クラスター関連は発症からポアソン分布となるが、市中感染者は４日目以降の標準偏差の大きなガウス分布になっている。
　一般的な感染症の発症から検査陽性確定までの陽性者数の時間推移は下記に示すようにポアソン分布となる。日本における新型コロナウィルスのＰＣＲ検査基準は発熱３７．５℃以上が四日間続く場合とされていたため、下記の示すようなガウス分布に準じている。

　下記に神奈川県と埼玉県の感染者情報の一部（発症日が公表されている事例）を基にグラフ化した。
サンプル数が少ないが、4月までの検査＆陽性確定は発症後検査が行われたが、市中感染（一般）は4日以降でないと検査陽性事例が少ない傾向になっている。
　5月以降はクラスター関連、市中感染者の区別なく発症後速やかに検査が行われた傾向が見られる。
感染から発症までの日数についても調査した感染者数は５名程度であったが平均３～４日以内であった。更なる調査を行えば日本における感染状況の把握に役立つ。
　以上を踏まえると今後の感染実態は4月以前の2週間前の異常状態から正常な状態となり、検査で現れた感染状況は6日～7日前の実態と推察できる。

Ⅴ．結論
　死亡率（１％）からの市中感染者を推定したが、精度及び信頼性を高めるためには、感染推移モデルで示した他症状（重傷者数、中等症数）の推移データが必要となる。現在、各自治体が公開している各症状のデータは病床の使用状況である。病床利用数も感染者の治療の観点から感染拡大時の一つの指標として重要であるが、感染症の全体把握のためには患者の最終症状の累計データが必要となる。総感染者数と市中感染者数の精度の高い推定値を算定する必要が急務である。
感染者数＝無症状者数＋軽症者数数＋中等症者数
　　　但し、重傷者数は中等症に含む。死亡者数は別扱とする。
患者の治療の観点から、病床の使用状況の指標として重要であるが、感染事前予測も重要である。
　病床の確保のためにも、数日前に確定感染者の数を予測する必要があり、本推論により数日前に感染者数が予測可能となり、病床の準備に対応できる。
　また、厚労省が行った抗体検査結果も検査手法から陽性数も信頼性はあるが、検査数不足と思われる。しかし、東京と大阪の合計数から都市部の陽性率（０．１～１．７％）は信頼できる。この結果から１～２万人が感染となり、本推論で推定した大阪の総感染者９０００件とほぼ一致する。
　また、確定陽性者の感染実態は２週間前の状態と推定しているが、データを基に議論すべきである。感染日,発症日,検査日,確定日,報告日のデータを市中感染者（リンク不明者）とクラスター関連者別に経過時間分析を行うことが、次の第２波感染時の対策に重要となる。

Ⅵ．終わりに
　３月から自粛生活を行いながら、放射線物理の情報処理の経験から新型コロナウィルス感染の解析を進め、市中感染者数を推測する方法を検討し、本件の理論となった。
　本論の考え方が、次期新型コロナウィルス感染の予防等に役立つことを望む。

参考文献
（１） 放射線計測　－計数の統計－
（２） H12　計算ウィルス学・免疫学の展開　九州大学大学院　理学研究部　ＪＳＴさきがけ　石見真吾