新型コロナ(COVID19)の関東7都県の感染状況の分析(更新日：2021年4月17日)

　関東７都県も大阪府や兵庫県と同様に第４波の感染爆発が始まった。既に第３波（12月25日の感染レベル）の感染状況と同じであり、今後は大阪府と同じ増加率で第３波の２～３倍の感染爆発が予想される。首都圏と同様に北関東（茨城、栃木、群馬）も感染増の傾向が見られる。
　2020年3月からの新型コロナの感染状況を可視化し、関東７都県の感染対策に必要な情報を公開する。
　関東の感染推移は3月初旬から5月末までの分布(ガウス分布):第１波と10月末までの連続したガウス分布:第２波と11月初旬からの分布:第３波であった。首都圏の第２波の推移は、関西、東海地方の首都圏以外が７月中旬から感染増加したのに対して、既に首都圏は6月初旬に感染増加が始まっていた。第２波の推移で7月中旬のわずかな減少はGoToキャンペーン(東京都以外が対象)で関東のスーパースプレッダーがGoTo利用や出張等で地方に旅行や出張した影響と思われる。第２波は全国的な８月初旬をピークとする分布(ガウス関数)とお盆休みの影響による分布及び緊急事態宣言の未発出と秋の行楽による影響と思われる。10月初旬からの第３波急増はGoToトラベル東京都追加により全国のスーパースプレッダーの行動拡大の影響と思われる。11月中旬からの傾向は、大阪市、札幌市の停止発表により人々の意識の高まりにより緩かな増加となったと思われる。しかし、正月からの急増は、全国的な傾向であり、クリスマス&師走の人々の外出の影響と思われ、緊急事態宣言の発出となった。
　関東7都県の感染傾向は東京都とほぼ同じであり、経済圏が同じ東京都と感染対策は連携して行うことが望ましい。

2．東京都の新型コロナ感染状況
　東京都の新型コロナ感染状況の可視化と市中感染者数の推移について分析した。
2.1 検査陽性者数と死亡者数の推移
　第３波の日毎の死亡者数の推移は検査陽性者数の推移の約３週間遅れて推移する傾向であった。第２波では約3~4週間遅れの傾向であった。
　既に掲載している『都道府県別の死亡率と高齢者率からみた感染状況の「傾向と対策」』で死亡者率は第１波:5.2%、第２波:0.6%、第３波:0.6%であった。

2.2高齢者数と死亡者数の推移
　高齢者数の推移と日毎の死亡者数の推移は検査陽性者とほぼ同様に2~3週間程度の遅れた推移であった、
　既に掲載している『都道府県別の死亡率と高齢者率からみた感染状況の「傾向と対策」』で高齢者率(75歳以上)は第１波:17.4%、第２波:5.6%、第３波:11.9%であった。また、高齢者数を母数とした死亡率は１波:29.8%、第２波:10.4%、第３波:4.8%であった。
　第２波の高齢者数と高齢者率はほぼ同じ傾向であったが、第３波では高齢者率は10%から20%と右肩上がりの傾向(2月中旬から減少)だが高齢者数の推移は1月中旬から減少傾向となった。

2.3死亡率からの市中感染者数の推定
　2020年7月に掲載『日本の新型コロナウイルス感染状況の考察』で死亡者数と死亡率及び推定市中感染者に対する検査率から市中感染者数の推定理論を公開している。
　①検査陽性者数の微分値曲線から最適化関数(ガウス関数)の標準偏差σ、ピーク値、平均値μ、FWHMの初期値を推定する。
　②死亡率(死亡者数/市中感染者数)の推定値を積極的な検査を行っている海外(米国等)の死亡者率:約１%、日本の医療技術の高さ、検査陽性者数に対する死亡率:0.6%を踏まえて0.5%~0.6%程度と仮定した。なお、総感染者数と検査陽性者数から検査率は50%程度であった。
　③上記初期値を前提に最小二乗法によりガウス関数で関数適合を行い感染分布の最適化関数を適合した。
　④感染者数から検査陽性者数と市中で回復した感染者数を引き算し、市中感染者数を推定した。また、簡易実行再生産数の推移を同時に示した。

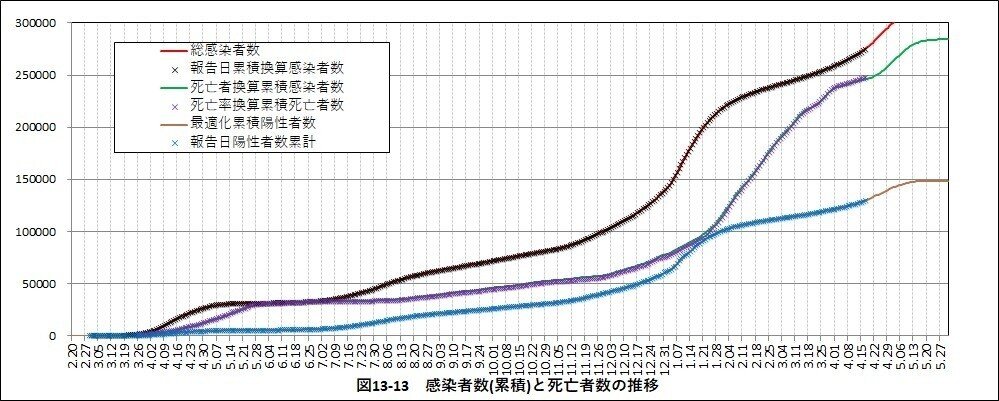
3．神奈川県の新型コロナ感染状況
　神奈川県の新型コロナ感染状況を可視化及び感染推移の最適化を行った。
3.1検査陽性者数と死亡者数の推移
　第２波の日毎の死亡者数の推移は検査陽性者数の推移の約３週間遅れて推移する傾向であった。第３波でも同じ傾向であった。
　既に掲載している『都道府県別の死亡率と高齢者率からみた感染状況の「傾向と対策」』で死亡者率は第１波:6.3%、第２波:1.2%、第３波:0.9%であった。死亡者数の推移は２週間毎のピークとなっていることが顕著に表れていた。

3.2高齢者数と死亡者数の推移
　高齢者数の推移と日毎の死亡者数の推移は、検査陽性者と同様に３週間程度の遅れた推移であった。
　既に掲載している『都道府県別の死亡率と高齢者率からみた感染状況の「傾向と対策」』で高齢者率(75歳以上)は第１波:16.3%、第２波:13.6%、第３波:15.2%であった。また、高齢者数を母数とした死亡率は１波:38.6%、第２波:8.5%、第３波:5.8%であった。
　東京都と同様に第２波の高齢者数と高齢者率はほぼ同じ傾向であったが、第３波では高齢者率は10%から20%と右肩上がりの傾向(2月中旬から減少)だが高齢者数の推移は1月中旬から減少傾向となった。

3.3死亡率からの市中感染者数の推定
　東京都と同じ解析法で市中感染者数を推定した。
　2020年7月に掲載『日本の新型コロナウイルス感染状況の考察』に死亡者数と死亡率及び推定市中感染者に対する検査率から市中感染者数の推定理論を公開している。
　①検査陽性者数の微分値曲線から最適化関数(ガウス関数)の標準偏差σ、ピーク値、平均値μ、FWHMの初期値を推定する。
　②死亡率(死亡者数/市中感染者数)の推定値を積極的な検査を行っている海外(米国等)の死亡者率:約１%、日本の医療技術の高さ、検査陽性者数に対する死亡率:0.9%を踏まえて0.6%~0.9%程度と仮定した。総感染者数と検査陽性者数から検査率は50%程度であった。
　③上記初期値を前提に最小二乗法によりガウス関数で関数適合を行い、感染分布の最適化関数を適合した。
　④感染者数から検査陽性者数と市中で回復した感染者数を引き算し、市中感染者数を推定した。また、簡易実行再生産数の推移を同時に示した。

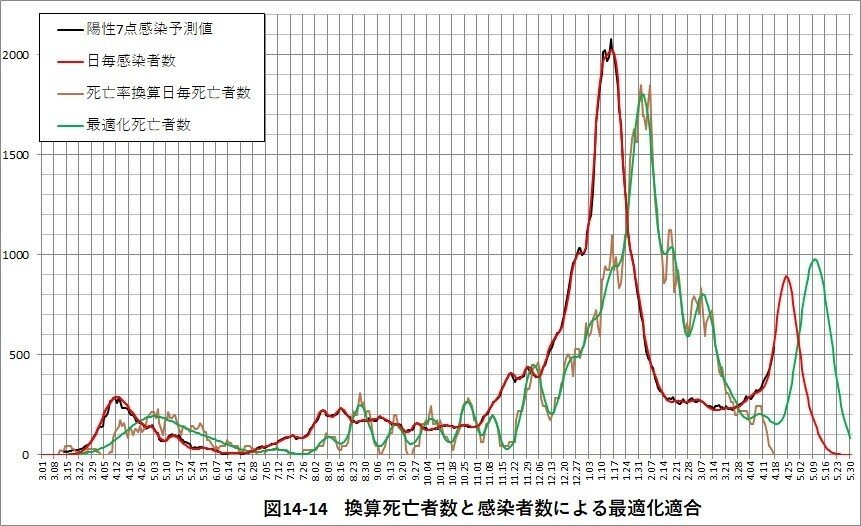
4．埼玉県の新型コロナ感染状況
　埼玉県の新型コロナ感染状況を可視化及び感染推移の最適化を行った。
4.1検査陽性者数と死亡者数の推移
　第２波の日毎の死亡者数の推移は検査陽性者数の推移の約３週間遅れて推移する傾向であった。第３波でも同じ傾向となった。
　既に掲載している『都道府県別の死亡率と高齢者率からみた感染状況の「傾向と対策」』で死亡者率は第１波:6.5%、第２波:1.1%、第３波:1.2%であった。

4.2高齢者数と死亡者数の推移
　高齢者数の推移と日毎の死亡者数の推移は、検査陽性者と同様に２～３週間程度の遅れた推移であった。。
　既に掲載している『都道府県別の死亡率と高齢者率からみた感染状況の「傾向と対策」』で高齢者率(75歳以上)は第１波:19.9%、第２波:8.2%、第３波:15.5%であった。また、高齢者数を母数とした死亡率は１波:32.5%、第２波:12.9%、第３波:7.2%であった。
　東京都と同様に第２波の高齢者数と高齢者率はほぼ同じ傾向であったが、第３波では高齢者率は10%から20%と右肩上がりの傾向(2月中旬から減少)だが高齢者数の推移は1月中旬から減少傾向となった。

4.3死亡率からの市中感染者数の推定
　東京都と同様に市中感染者数を推定した。
　2020年7月に掲載『日本の新型コロナウイルス感染状況の考察』に死亡者数と死亡率及び推定市中感染者に対する検査率から市中感染者数の推定理論を公開している。
　①検査陽性者数の微分値曲線から最適化関数(ガウス関数)の標準偏差σ、ピーク値、平均値μ、FWHMの初期値を推定する。
　②死亡率(死亡者数/市中感染者数)の推定値を積極的な検査を行っている海外(米国等)の死亡者率:約１%、日本の医療技術の高さ、検査陽性者数に対する死亡率:1.1%~1.2%を踏まえて0.6%~0.8%程度と仮定した。総感染者数と検査陽性者数から検査率は50%程度であった。
　③上記初期値を前提に最小二乗法によりガウス関数で関数適合を行い、感染分布の最適化関数を適合した。
　④感染者数から検査陽性者数と市中で回復した感染者数を引き算し、市中感染者数を推定した。また、簡易実行再生産数の推移を同時に示した。

5．千葉県の新型コロナ感染状況
　千葉県の新型コロナ感染状況は　東京都と同じ経済圏のため影響が強く、感染分布も11月初旬から急増した分布とクリスマス&師走の外出による１月の分布となっていた。感染状況の可視化及び感染推移の最適化を行った。
5.1検査陽性者数と死亡者数の推移
　第2、3波の日毎の死亡者数の推移は検査陽性者数の推移の約2~3週間遅れて推移する傾向であった。
　既に掲載している『都道府県別の死亡率と高齢者率からみた感染状況の「傾向と対策」』で死亡者率は第１波:5.0%、第２波:1.0%、第３波:0.9%であった。

5.2高齢者数と死亡者数の推移
　高齢者数の推移と日毎の死亡者数の推移は、検査陽性者と同様に2~3週間程度の遅れた推移であった。
　既に掲載している『都道府県別の死亡率と高齢者率からみた感染状況の「傾向と対策」』で高齢者率(75歳以上)は第１波:17.9%、第２波:10.1%、第３波:14.0%であった。また、高齢者数を母数とした死亡率は１波:28.1%、第２波:9.8%、第３波:6.8%であった。
　東京都と同様に第２波の高齢者数と高齢者率はほぼ同じ傾向であったが、第３波では高齢者率は10%から25%と右肩上がりの傾向(2月中旬から減少)だが高齢者数の推移は1月中旬から減少傾向となった。

5.3死亡率からの市中感染者数の推定
　東京都と同様に市中感染者を推定した。
　2020年7月に掲載『日本の新型コロナウイルス感染状況の考察』に死亡者数と死亡率及び推定市中感染者に対する検査率から市中感染者数の推定理論を公開している。
　①検査陽性者数の微分値曲線から最適化関数(ガウス関数)の標準偏差σ、ピーク値、平均値μ、FWHMの初期値を推定する。
　②死亡率(死亡者数/市中感染者数)の推定値を積極的な検査を行っている海外(米国等)の死亡者率:約１%、日本の医療技術の高さ、検査陽性者数に対する死亡率:1.0%を踏まえて0.6%~0.8%程度と仮定した。総感染者数と検査陽性者数から検査率は50%程度であった。
　③上記初期値を前提に最小二乗法によりガウス関数で関数適合を行い、感染分布の最適化関数を適合した。
　④感染者数から検査陽性者数と市中で回復した感染者数を引き算し、市中感染者数を推定した。また、簡易実行再生産数の推移を同時に示した。

6．栃木県の新型コロナ感染状況
　栃木県の新型コロナ感染状況は　首都圏の影響が強く、感染分布も首都圏と同様の分布になっていた。感染状況の可視化及び感染推移の最適化を行った。
6.1検査陽性者数と死亡者数の推移
　第3波の日毎の死亡者数の推移は検査陽性者数の推移の約2~3週間遅れて推移する傾向であった。

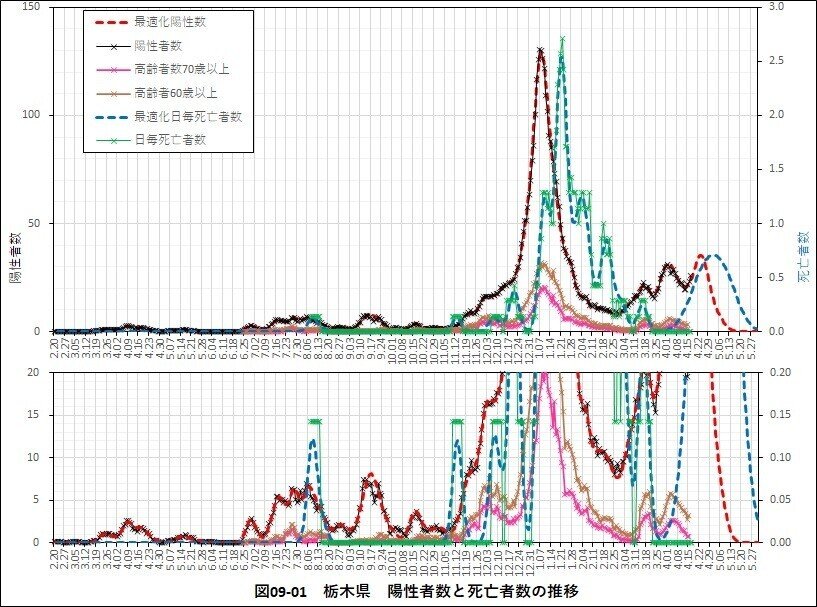
6.2高齢者数と死亡者数の推移
　高齢者数の推移と日毎の死亡者数の推移は、検査陽性者と同様に2~3週間程度の遅れた推移であった、第２波においては高齢者の検査陽性者数が少なかったため、死亡者数も非常に少なかった。

6.3死亡率からの市中感染者数の推定
　東京都と同様に市中感染者を推定した。参考に検査陽性者数の微分値曲線と死亡率換算感染者数の推移図を示した。
　死亡率及び検査率を前提として最適化関数(ガウス関数)適合結果と簡易実行再生産数と市中感染者数の推移を示した。

7．茨城県の新型コロナ感染状況
　茨城県の新型コロナ感染状況は　首都圏の影響が強く、感染分布も首都圏と同様の分布になっていた。感染状況の可視化及び感染推移の最適化を行った。
7.1検査陽性者数と死亡者数の推移
　第3波の日毎の死亡者数の推移は検査陽性者数の推移の約2~3週間遅れて推移する傾向であった。

7.2高齢者数と死亡者数の推移
　高齢者数の推移と日毎の死亡者数の推移は、検査陽性者と同様に2~3週間程度の遅れた推移であった。首都圏と同様の推移であった。

7.3死亡率からの市中感染者数の推定
　東京都と同様に市中感染者を推定した。参考に検査陽性者数の微分値曲線と死亡率換算感染者数の推移図を示した。
　死亡率及び検査率を前提として最適化関数(ガウス関数)適合結果と簡易実行再生産数と市中感染者数の推移を示した。

8．群馬県の新型コロナ感染状況
　群馬県の新型コロナ感染状況は検査陽性者数が首都圏より少なく、感染増加減少が顕著に表れていた。第２波の感染分布は、8月中旬、9月中旬、10月中旬の統計分布(ガウス分布)であった。第３波は首都圏と同様な分布になっていた。感染状況の可視化及び感染推移の最適化を行った。
8.1検査陽性者数と死亡者数の推移
　第3波の日毎の死亡者数の推移は検査陽性者数の推移の約2~3週間遅れて推移する傾向であった。

8.2高齢者数と死亡者数の推移
　高齢者数の推移と日毎の死亡者数の推移は、検査陽性者と同様に2~3週間程度の遅れた推移であった、第２波においては高齢者の検査陽性者数が少なく、死亡者数も非常に少なかった。

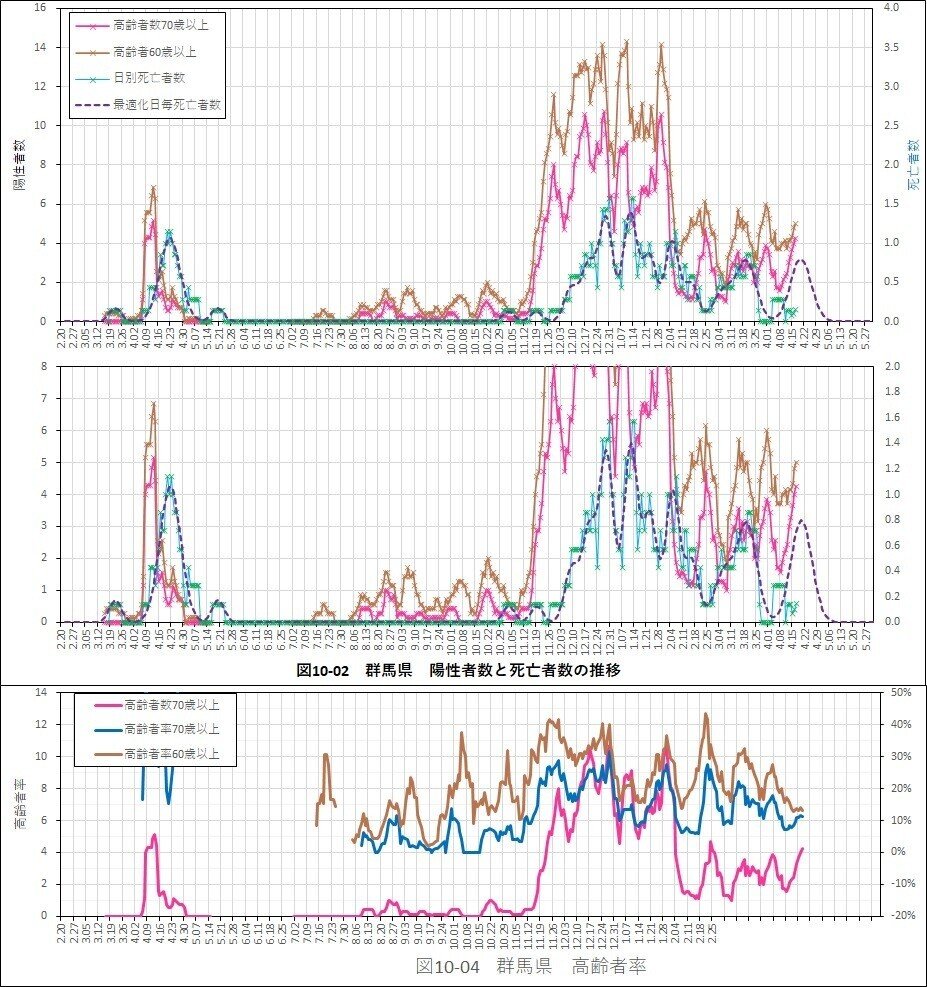
8.3死亡率からの市中感染者数の推定
　東京都と同様に市中感染者を推定した。参考に検査陽性者数の微分値曲線と死亡率換算感染者数の推移図を示した。
　死亡率及び検査率を前提として最適化関数(ガウス関数)適合結果と簡易実行再生産数と市中感染者数の推移を示した。

9．死亡者率と高齢者率
　全国主要都道府県別の死亡者率と高齢者率を示す

10．考察
　日毎の死亡者数の推移は、検査陽性者数の推移から2~3週間程度の遅れている。日毎の死亡者数の推移は、３週間程度の周期でピークとなり、陰陽暦の周期や月の満ち欠け周期なのか？
　東京都のGoToトラベル対処外(7月)対象(10月)、札幌市と大阪市のGoToトラベル停止要請(11月)、名古屋市と東京都のGoToトラベル停止要請(11月)による影響は①7月中旬から全国的感染拡大、②11月から第２波以上の感染拡大③11月の停止要請により国民の自粛意識の高まりにより全国的に増加の高止まりや減少傾向、などの結果が顕著に現れている。
　簡易実行再生産数計算法は放射線物理の散乱理論を参考に、直近一週間の検査陽性者数と二週前の週間検査陽性者数の行列係数と行動係数(行列)から行列計算されるため、感染分布(ガウス関数)関数の変移点で実行再生産数が1.0以下となる。