
バンブラP打ち込みテク紹介 その2 テンポ変更編
バンブラPアドベントカレンダー2022参加記事です。初日に書き上げる予定が、書く内容が増えに増えて大遅刻しました(土下座)。
今回の記事では、そのままではバンブラで打ち込むのが難しいリズムをテンポ変更を駆使して再現する方法を紹介します。
(今回は使い方のややこしいものも入っているため、手元のバンブラで試しながらゆっくり読み進めることを推奨します。)
計算式
テンポの値を求めるのに使う計算式は以下。(どうしてこの式で求められるか、導出過程は記事末尾のおまけを参照。)
テンポ変換の式
「元のリズム」と「バンブラ上でのリズム」で
$$
\frac{1}{テンポ}\times\frac{何個分}{何分音符}
$$
の値が一致するように設定する。
単純な倍速
まず公式の使い方を確認するために、簡単な例を公式を使って求めてみる。
32分音符を16分音符で打ち込む

テンポを$${2}$$倍にすることで打ち込めることが知られている。実際に公式に代入してみる。
元のリズム:テンポ(前)、32分音符、1個分
バンブラ上のリズム:テンポ(後)、16分音符、1個分
として、この値を公式に代入してみると、
元のリズムでは
$$
\frac{1}{テンポ}\times\frac{何個分}{何分音符} = \frac{1}{テンポ_前} \times \frac{1(個分)}{32(分音符)}
$$
バンブラ上のリズムでは
$$
\frac{1}{テンポ}\times\frac{何個分}{何分音符} = \frac{1}{テンポ_後}\times\frac{1(個分)}{16(分音符)}
$$
この2つの値が一致してほしいので、
$$
\frac{1}{テンポ_前} \times \frac{1(個分)}{32(分音符)} = \frac{1}{テンポ_後}\times\frac{1(個分)}{16(分音符)}
$$
これを テンポ(後) = … の形になるように変形すると、
$$
テンポ_後 = 2 \times テンポ_前
$$
つまりバンブラ上のテンポを元の$${2}$$倍に設定すればいいことがわかる。
6連符(24分音符)を16分音符で打ち込む

こちらはテンポを$${1.5}$$倍にすることで打ち込める。
6連符は4分音符を6等分した長さなので、「4分音符$${1/6}$$個分」と考えて公式に代入する。(「8分音符$${1/3}$$個分」や「24分音符$${1}$$個分」として計算しても同じ結果になるので、考えやすい方法を使ってOK)
元のリズム:テンポ(前)、4分音符、$${1/6}$$個分
バンブラ上のリズム:テンポ(後)、16分音符、$${1}$$個分
として、この値を公式に代入してみると
$$
\frac{1}{テンポ_前} \times \frac{1/6(個分)}{4(分音符)} = \frac{1}{テンポ_後}\times\frac{1(個分)}{16(分音符)}
$$
これを テンポ(後) = … の形になるように変形すると、
$$
テンポ_後 = \frac 3 2 \times テンポ_前
$$
つまりバンブラ上のテンポを元の$${1.5}$$倍に設定すればいいことがわかる。
その他、色々な倍速
この他にも色々なリズムを公式を使って変換できる。
3連符を16分音符で打ち込む → $${0.75}$$倍 (3連符しかない4/4拍子曲を3/4拍子に詰め込むときの設定)
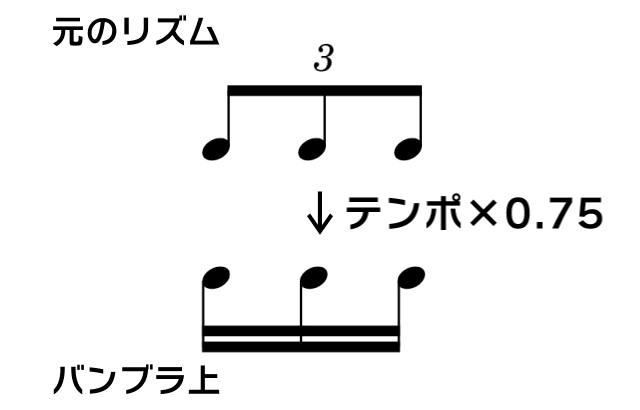
$$
\frac{1}{テンポ_前} \times \frac{1/3(個分)}{4(分音符)} = \frac{1}{テンポ_後}\times\frac{1(個分)}{16(分音符)}
$$
付点8分・付点8分・8分のリズムを3連符で打ち込む → $${4/9}$$倍・$${4/9}$$倍・$${2/3}$$倍 (全体を半分のテンポで打ち込んでるときに、このリズムのためだけに元のテンポに戻したくないときの設定)
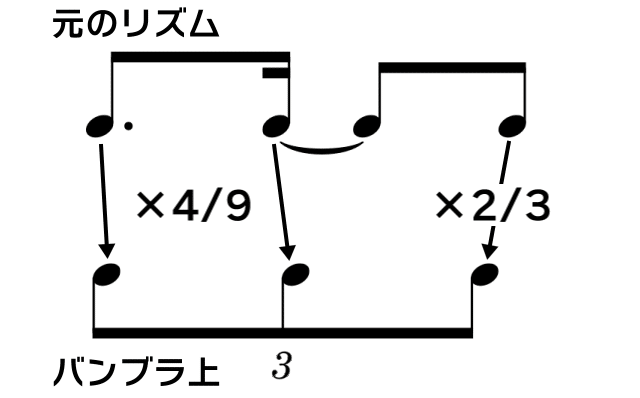
1, 2音目:付点8分を3連符で
$$
\frac{1}{テンポ_前} \times \frac{3(個分)}{16(分音符)} = \frac{1}{テンポ_後}\times\frac{1/3(個分)}{4(分音符)}
$$
3音目:8分を3連符で
$$
\frac{1}{テンポ_前} \times \frac{1(個分)}{8(分音符)} = \frac{1}{テンポ_後}\times\frac{1/3(個分)}{4(分音符)}
$$
16分音符と3連符を組み合わせる
16分音符と3連符のリズムの微妙なズレを、テンポ変更を駆使して整えることで、より細かいリズムを作ることができる。
16分音符と3連符はどのくらいズレてる?
計算に使うために、まず16分音符と3連符のズレがどの程度か($${\frac{何個分}{何分音符}}$$の値がいくつか)求めてみると、以下のようになる。(導出過程は記事末尾のおまけを参照)

テンポ設定の打ち込み方
16分モードでは①②④⑥のテンポを、3連符モードでは①③⑤のテンポを入力することができる。


カーソルに幅があってどこのテンポを指してるのかわかりづらいが、カーソルの左端のタイミングで変わると考えるとわかりやすい。(ちなみに、音量変更・音色変更の実際に変わるタイミングも同様)
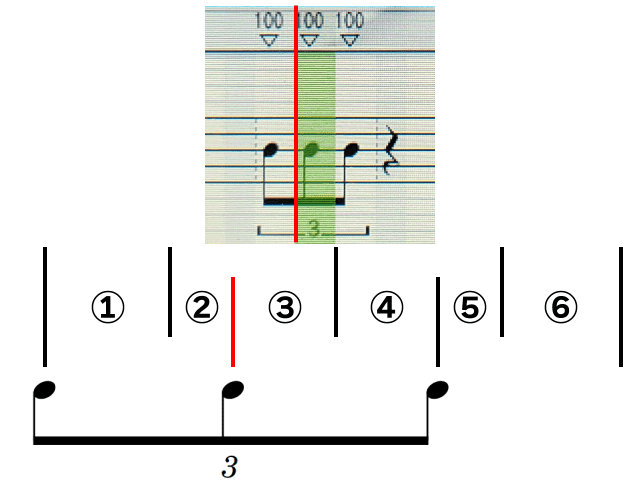
6連符を作る
それぞれの間隔が「4分音符$${1/6}$$個分」と等しくなるように計算してみると、
$${\frac{1}{テンポ_前} \times \frac{1/6}{4} = \frac{1}{テンポ_後}\times\frac{1}{16} \quad\to\quad テンポ_後 = \frac{3}{2} \times テンポ_前}$$
$${\frac{1}{テンポ_前} \times \frac{1/6}{4} = \frac{1}{テンポ_後}\times\frac{1}{48} \quad\to\quad テンポ_後 = \frac{1}{2} \times テンポ_前}$$
$${\frac{1}{テンポ_前} \times \frac{1/6}{4} = \frac{1}{テンポ_後}\times\frac{1}{24} \quad\to\quad テンポ_後 = テンポ_前}$$
$${\frac{1}{テンポ_前} \times \frac{1/6}{4} = \frac{1}{テンポ_後}\times\frac{1}{24} \quad\to\quad テンポ_後 = テンポ_前}$$
$${\frac{1}{テンポ_前} \times \frac{1/6}{4} = \frac{1}{テンポ_後}\times\frac{1}{48} \quad\to\quad テンポ_後 = \frac{1}{2} \times テンポ_前}$$
$${\frac{1}{テンポ_前} \times \frac{1/6}{4} = \frac{1}{テンポ_後}\times\frac{1}{16} \quad\to\quad テンポ_後 = \frac{3}{2} \times テンポ_前}$$
と、左から順に元のテンポの $${1.5}$$倍, $${0.5}$$倍, $${1}$$倍, $${1}$$倍, $${0.5}$$倍, $${1.5}$$倍 となる。

一番倍率の高いところで$${1.5}$$倍なので、テンポ200まで打ち込むことができる。このテンポの上限は単純な倍速で紹介した方法と変わらない。
32分音符を作る
間隔の②~⑤が狭いことを利用して、ここで32分を打ち込むことを考えてみる。
倍率を計算してみると、
等倍
$${\frac{1}{テンポ_前} \times \frac{1}{32} = \frac{1}{テンポ_後}\times\frac{1}{48} \quad\to\quad テンポ_後 = \frac{2}{3} \times テンポ_前}$$
$${\frac{1}{テンポ_前} \times \frac{1}{32} = \frac{1}{テンポ_後}\times\frac{1}{24} \quad\to\quad テンポ_後 = \frac{4}{3} \times テンポ_前}$$
$${\frac{1}{テンポ_前} \times \frac{1}{32} = \frac{1}{テンポ_後}\times\frac{1}{24} \quad\to\quad テンポ_後 = \frac{4}{3} \times テンポ_前}$$
$${\frac{1}{テンポ_前} \times \frac{1}{32} = \frac{1}{テンポ_後}\times\frac{1}{48} \quad\to\quad テンポ_後 = \frac{2}{3} \times テンポ_前}$$
等倍
と、左から順に元のテンポの 1倍, $${2/3}$$倍, $${4/3}$$倍, $${4/3}$$倍, $${2/3}$$倍, 1倍 となる。

一番倍率の高いところでも$${4/3}$$倍なので、テンポ225までの32分音符を打ち込むことができる。32分音符4連までしか打ち込めないが、単純な倍速よりも速いテンポで打ち込めるようになる。
補足
計算結果に小数が含まれてしまったときの対処法
バンブラではテンポを整数でしか打ち込めないため、計算結果が小数となった場合はひと工夫する必要がある。
ここではテンポ123の1.5倍でテンポ184.5を入力したいときを例に考える。
1. 単に四捨五入する
この場合、184.5の代わりに185を入力する。
シンプル。若干テンポが変わってしまうのが難点だが、テンポが速いほどこの差は小さくなるので、ある程度速い曲なら気にならないかも。そもそもバンブラのテンポってそこまで正確じゃないし。(おまけ参照)
2. 曲全体のテンポを変える
この場合、曲のテンポの方を1.5倍しても整数になる122や124に設定する。
曲全体のテンポを、x倍しても整数になるように設定してしまうという方法。原曲と比べて全体的に早く/遅くなるのが気になる可能性はあるが、曲全体を通しての違和感はなくなる。
3. 前後の値を交互に配置する
この場合、184.5のところに184と185を交互に入力する。
全体的なテンポをより正確にしたいときに有効。交互に置く区間が長いときは変更回数の上限に注意。良くも悪くも、演奏中にテンポが変わっている区間が目立つという副作用もある。
テンポ変更が一瞬だけの場合は使えない。この場合は、次節「発展」で紹介する方法を使おう。
「単純な倍速」と「16分+3連符」の比較
16分音符と3連符を組み合わせて打ち込む方法の長所・短所をまとめる
長所
バンブラ上でも1拍の中に6音を詰め込めるので、6連符が続いても拍がズレない。
小節数の節約にもなる。
使い方次第で、単純な倍速では再現できないリズムを打ち込める。
短所
1拍にテンポ変更を詰め込むので、テンポ変更回数を大量に消費する。
2パート必要になる可能性が高い。
打ち込みが面倒。
「16分+3連符」を使う時に設定したい音量変更
単音のフレーズを2パート使って16分音符と3連符に分けて打ち込むとき、音量変更を設定しないと2つの音が同時に鳴ってしまい違和感が出ることがある。
下のように音量変更で細かく音のON/OFFを切り替えることで、同時に鳴るのは1音までになり、違和感がかなり解消される。

設定が重なりすぎて見づらくなったテンポの値の確認
16分と3連符の両方にテンポを入力すると、入力した値が非常に見づらくなってしまうことがある。

そんなときは、カーソルを合わせて上画面を見ることで値を確認することができる。
カーソルに幅があってどこのテンポを指してるのかわかりづらいが、カーソルの左端のテンポを指してる考えるとわかりやすい。かも。

計算面倒なんだが?
方程式を解いてくれるツールを使いましょう。
Webページ Wolfram|Alpha - https://www.wolframalpha.com/

スマホアプリ Photomath - https://photomath.com/

発展
テンポ変換の式の拡張
テンポ変換の式は和の形でも考えることができる。つまり、
$${ \frac{1}{テンポ}\times\frac{何個分}{何分音符} }$$の和が、「元のリズム」と「バンブラ上でのリズム」で一致するように設定する。
と言い換えられる。これを使うと更に色々なリズムをバンブラで再現できるようになる。
いくつか実際の計算例を見ていく。この節の計算は全て、答えが「元のテンポの○○倍」という形で書けないものになるため、ここで紹介する手順を参考にして曲ごとに計算し直すことになる。
「16分と3連符を使って6連符」をテンポ200超えで使う
テンポ204で以下のリズムをこれまでの方法で打ち込もうとすると、⑥がテンポ306となり、バンブラで打ち込める上限テンポ300を超えてしまう。

そこで、テンポ300を超えてしまった⑥をテンポ300に設定し、生まれたズレをその前後⑤のテンポを変更して吸収することを考える。

この⑤に入れるテンポをいくつにするか、和の式を使って求めていく。
元のリズム:テンポ204・6連符・1個分 が2個
だから、
$$
\frac{1}{テンポ}\times\frac{何個分}{何分音符} の和 = \frac{1}{204}\times\frac{1/6}{4} + \frac{1}{204}\times\frac{1/6}{4}
$$
バンブラ上のリズム:テンポ$${x}$$・$${1/48}$$ と テンポ300・$${1/16}$$
だから、
$$
\frac{1}{テンポ}\times\frac{何個分}{何分音符} の和 = \frac{1}{x}\times\frac{1}{48} + \frac{1}{300}\times\frac{1}{16}
$$
この2つの値が一致してほしいので、
$$
\frac{1}{204}\times\frac{1/6}{4} + \frac{1}{204}\times\frac{1/6}{4} = \frac{1}{x}\times\frac{1}{48} + \frac{1}{300}\times\frac{1}{16}
$$
これを解いて、
$$
x = \frac {5100}{49} \fallingdotseq 104
$$
よって、⑤のテンポは104に設定すればいい。

「○分音符」という形で表しにくい音
アルペジオやグリッサンド等をできるだけ速く鳴らしたいときの計算。ここではアルペジオを例に計算してみる。
以下のように3音のアルペジオを16分音符の3音目と12分音符の2・3音目に対応させて打ち込んでいく。

③④の間隔をできるだけ短くしたいので、③④のテンポを300に設定する。
拍頭~アルペジオの長さ、アルペジオ~次の拍頭の長さがともにテンポ176の8分音符と同じになるように①②と⑤⑥の値を計算していく。

左の組:
元のリズムではテンポ176の8分音符1個分で$${\frac{1}{176}\times\frac{1}{8}}$$、
バンブラ上のリズムではテンポ$${x}$$・$${1/16}$$とテンポ$${x}$$・$${1/48}$$とテンポ300・$${1/24}$$で$${\frac{1}{x}\times\frac{1}{16} + \frac{1}{x}\times\frac{1}{48} + \frac{1}{300}\times\frac{1}{24}}$$
この2つが一致してほしいので、
$$
\begin{align*}
\frac{1}{176}\times\frac{1}{8} &= \frac{1}{x}\times\frac{1}{16} + \frac{1}{x}\times\frac{1}{48} + \frac{1}{300}\times\frac{1}{24}\\
\therefore \quad x &= \frac{26400}{181} \fallingdotseq 146
\end{align*}
$$
右の組についても全く同じ計算になって、①②⑤⑥のテンポを146にすればいいことがわかる。

「8分音符」と「付点8分+付点8分+8分」のリズムを半分のテンポで1拍に詰め込む
以下のような2拍分のリズムを、テンポ変更を駆使して1拍に打ち込むことができる。
「小節数節約のためにテンポ半分にしてるけど、このリズムのためだけにテンポを元に戻したくない……」というときに使える。
今回はテンポ180で、8分音符のリズムを中心に組み立てていく。
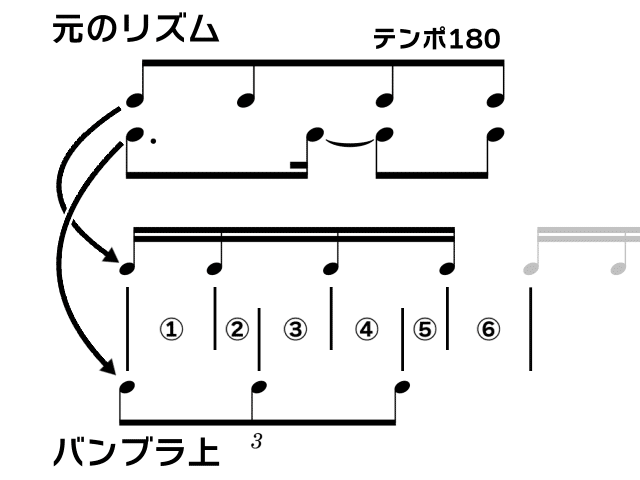
まず⑤の両端の音、16分音符4つ目と3連符3つ目は元のリズムで同時に鳴る音のため、ここのテンポを300に設定する。
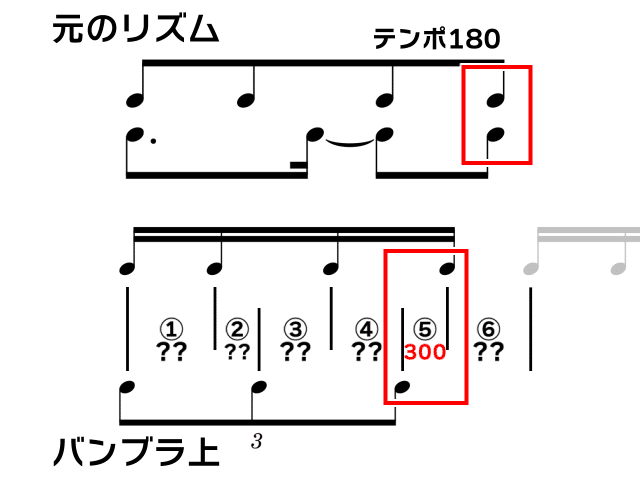
ここにテンポ300を設定した分のズレを④か⑥で吸収する。今回は8分音符のリズムを中心に考えるため、④+⑤の長さが元のリズムの8分音符から変わらないようにする。
$$
\begin{align*}
\frac{1}{180}\times\frac{1}{8} &= \frac{1}{x}\times\frac{1}{24} + \frac{1}{x}\times\frac{1}{48} \\
\therefore \quad x &= \frac{200}{3} \fallingdotseq 67
\end{align*}
$$
よって、④のテンポを67にする。

残りの①②③⑥テンポは、1音の計算で求まる。
①:元8分音符をバンブラ上16分音符で→0.5倍のテンポ90
②:元16分音符をバンブラ上1/48の長さで→1/3倍のテンポ60
③:元16分音符をバンブラ上1/24の長さで→2/3倍のテンポ120
⑥:元8分音符をバンブラ上16分音符で→0.5倍のテンポ90

単純な倍速の16分3連符と同時に16分音符
8分音符→16分3連符のリズムを全て16分音符で打ち込み、テンポを0.5倍→1.5倍として打ち込む方法に、同時に8分音符→16分音符2つのリズムを3連符で埋め込むことができる。
ここではテンポ160で、8分音符→16分3連符のリズムを中心に組み立てることを考える。

まず、①と⑥はそのままの値を使える。
次に②の両端の音、16分音符2つ目と3連符2つ目は元のリズムで同時に鳴る音のため、ここのテンポを300に設定する。

②+③の長さがテンポ160の16分3連符1個と同じになってほしいので、
$$
\begin{align*}
\frac{1}{160}\times\frac{1/3}{8} &= \frac{1}{300}\times\frac{1}{48} + \frac{1}{x}\times\frac{1}{24} \\
\therefore \quad x &= \frac{2400}{11} \fallingdotseq 218
\end{align*}
$$
よって、③のテンポは218にする。
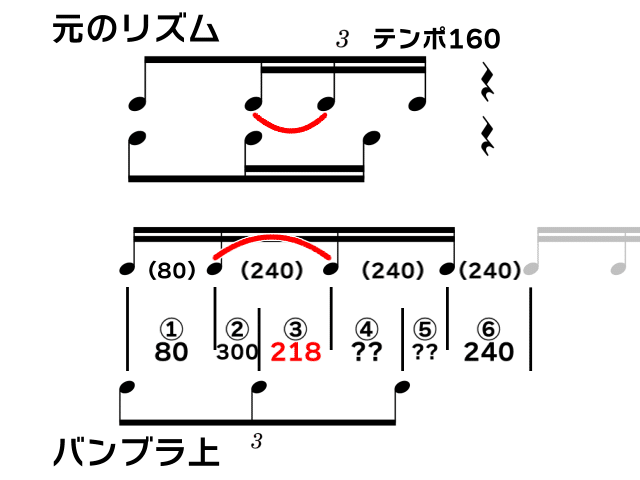
④⑤の求め方は色々考えられるが、今回は後ろから和で求めていく。
(他には先頭から和で求める方法、16分3連-16分音符の間隔を求めてから比を求める方法がある。詳細は割愛)
まず⑤+⑥の長さがテンポ160の16分音符1個と同じになってほしいので、
$$
\begin{align*}
\frac{1}{160}\times\frac{1}{16} &= \frac{1}{x}\times\frac{1}{48} + \frac{1}{240}\times\frac{1}{16} \\
\therefore \quad x &= 160
\end{align*}
$$
よって、⑤のテンポは160にする。

次に④+⑤の長さがテンポ160の16分3連符1個と同じになってほしいので、
$$
\begin{align*}
\frac{1}{160}\times\frac{1}{24} &= \frac{1}{x}\times\frac{1}{24} + \frac{1}{160}\times\frac{1}{48} \\
\therefore \quad x &= 320
\end{align*}
$$
④のテンポが320となり、300を超えてしまう。④のテンポを300にして、前後の③か⑤のテンポでズレを吸収することを考える。
今回は16分3連符のリズムを中心に考えるため、④+⑤の長さが変わらないように⑤のテンポを変更することで調整する。
$$
\begin{align*}
\frac{1}{160}\times\frac{1}{24} &= \frac{1}{300}\times\frac{1}{24} + \frac{1}{x}\times\frac{1}{48} \\
\therefore \quad x &= \frac{1200}{7} \fallingdotseq 171
\end{align*}
$$
よって、④をテンポ300、⑤をテンポ171にする。

計算結果に小数が含まれてしまったときの対処法④
下図のようにテンポが小数になってしまったとき、テンポが遅いため単に四捨五入するだけでは実際のリズムとの差が大きくなってしまうことがある。
これを、前後のテンポが速い部分を利用して、和の公式で補正していく。
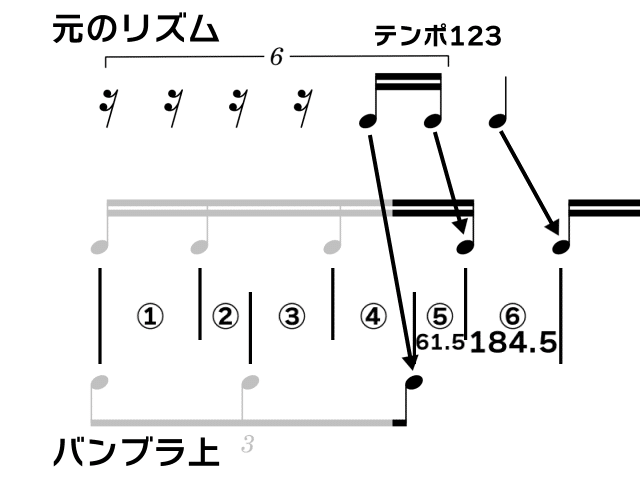
まず、問題となるテンポが遅い部分を四捨五入する。(⑤:61.5→62)
次に、前後のテンポが速い部分と組み合わせて、長さが元のリズムと変わらないように計算する。
今回は⑤+⑥=テンポ123の6連符2個分なので
$$
\begin{align*}
\frac{1}{123}\times\frac{2/6}{4} &= \frac{1}{62}\times\frac{1}{48} + \frac{1}{x}\times\frac{1}{16} \\
\therefore \quad x &= \frac{1200}{7} \fallingdotseq 183.024
\end{align*}
$$
ここでテンポ300を超えてしまった場合は、遅い部分のテンポを1上げて再計算する。
最後に結局四捨五入して完成。(⑥:183.024→183)

おまけ
細々とした補足や蛇足、どこに入れるか迷ったことなど
計算式の導出
「テンポと音符の種類から、その音符が占める実時間の長さはどれくらいか?」を考えてみる。
テンポは「1分間に刻める4分音符の個数」だから、4分音符1個分の長さは$${ \frac{60}{テンポ} (秒) }$$となる。
ここから音符を種類を変えてみる。
16分音符1個のときの長さは4分音符1個のときの長さの$${1/4}$$倍、2分音符1個のときの長さは4分音符1個のときの長さの$${2}$$倍と変化する。
$${1/4}$$倍・$${2}$$倍をそれぞれ$${4/16}$$倍、$${4/2}$$倍と考えると、○分音符のとき$${4/○}$$倍と考えることができる。
まとめると、○分音符1個分の長さは$${ \frac{60}{テンポ} \times \frac{4}{○分音符} (秒) }$$となる。
さらに、個数の倍にしたら当然長さも倍になるので、○分音符1個分の長さは$${ \frac{60}{テンポ} \times \frac{4}{○分音符} \times ○個分 = 240 \times \frac{1}{テンポ} \times \frac{○個分}{○分音符} (秒)}$$となる。
ここで当初の目的を思い出すと、元のリズムとバンブラでのリズムを一致させることだった。これを達成するためには、元のリズムとバンブラでのリズムで音の長さを一致させればいい。
よって、
$$
\begin{align*}
音の長さ_前 &= 音の長さ_後 \\
240 \times \frac{1}{テンポ_前} \times \frac{○個分_前}{○分音符_前} (秒) &= 240 \times \frac{1}{テンポ_後} \times \frac{○個分_後}{○分音符_後} (秒) \\
\frac{1}{テンポ_前} \times \frac{○個分_前}{○分音符_前} &= \frac{1}{テンポ_後} \times \frac{○個分_後}{○分音符_後}
\end{align*}
$$
つまり、「$${\frac{1}{テンポ} \times \frac{○個分}{○分音符}}$$が元のリズムとバンブラで一致するように設定すればOK」ということ。
この計算は複数個の音符の和で考えても同様。数式の形で表すなら、「$${\sum_i \frac{1}{テンポ_i} \times \frac{○個分_i}{○分音符_i}}$$が元のリズムとバンブラで一致するように設定すればOK」となる。
計算式の解釈
$${\frac{何個分}{何分音符}}$$の部分は「全音符の長さを1としたときの、その音符の長さ」とも言える。この「音符の長さ」を「音価」としてまとめると、計算式は「$${\frac{音価}{テンポ}}$$を一致させる」と言い換えられて表現がスッキリする。
式の意味は変わらないので、覚えやすい方でどうぞ。
○分音符の拡張
○分音符の○には通常、1(全), 2, 4, 8, 16, …と2の累乗の数しか入らない。
しかし、○分音符を「(4/4拍子の)1小節を○等分する長さの音符」と考えると、
3連符(1拍を3等分)=「1小節を12等分する長さ」= 12分音符
6連符(1拍を6等分)=「1小節を24等分する長さ」= 24分音符
と捉えることができる。
この2の累乗でない○分音符で考えても今回の計算式は正しく機能するので、音ゲー等でこの表現に慣れてる人も気にせず計算に使ってOK
更に拡張させると
付点8分音符 =「3小節を16等分する長さ」= $${\frac{16}{3}}$$分音符
という表現もできる。(ナニコレ?)
16分音符と3連符のズレ量の計算
16分音符は1拍の 0, 1/4, 1/2, 3/4 のタイミングで、3連符は1拍の 0, 1/3, 2/3 のタイミングで発音する。
これをまとめると、発音のタイミングは 0, 1/4, 1/3, 1/2, 2/3, 3/4 の6つになる。

それぞれの間隔は
① 0 → 1/4 : 1/4 - 0 = 1/4
② 1/4 → 1/3 : 1/3 - 1/4 = 1/12
③ 1/3 → 1/2 : 1/2 - 1/3 = 1/6
……以下同様
よって、それぞれ1拍の 1/4, 1/12, 1/6, 1/6, 1/12, 1/4 の長さになる。
これは○分音符1個分の言い方に直すと、○はそれぞれ 16分, 48分, 24分, 24分, 48分, 16分となり、
48分音符○個分の言い方に直すと、それぞれ 3, 1, 2, 2, 1, 3個となる。
理論と実機の違い
バンブラ上ではこの計算通りの長さで音が鳴ってくれるとは限らない。
例えば、テンポ180で3拍毎に(=1秒に1回の頻度で)ハイハットを入力した音源で、バンブラ上のハイハットのタイミングと理論値とのズレを計測してみると……
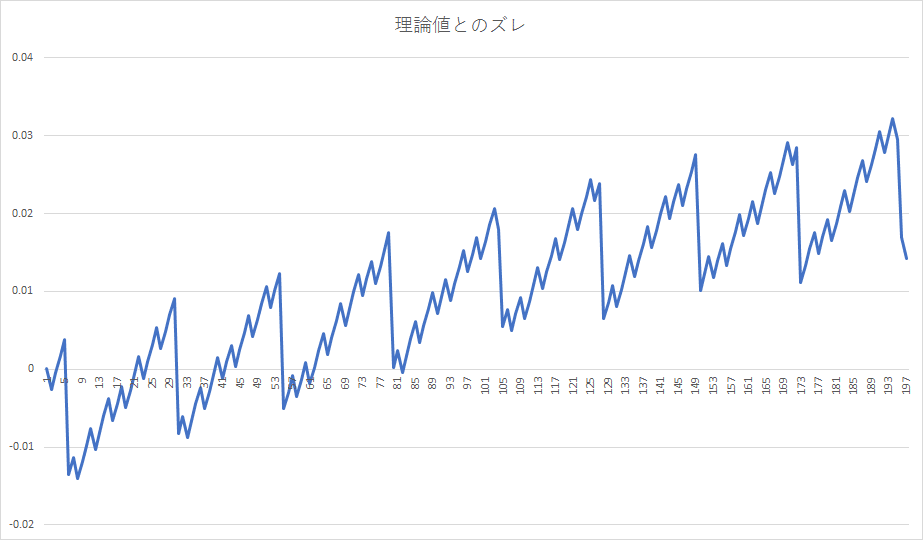
大きな差ではないが、僅かにズレが発生してしまう。(実際にどんな法則でズレが生まれるかは未解決。今後の課題とするとかなんとか)
ズレが気になったら適宜テンポを±1したりして調整しよう。
また、曲を再生する場面(作曲画面・パート選択画面・演奏中……etc)によってもテンポが変化している。
(動画化する際、録音したデータと演奏画面の譜面がズレる場合は、演奏画面を録画するときにテンポを1上げるとズレが直ることもある。)
参考
モード/作曲 - 大合奏!バンドブラザーズP まとめ Wiki* https://wikiwiki.jp/bandbrosp/%E3%83%A2%E3%83%BC%E3%83%89/%E4%BD%9C%E6%9B%B2#y194e2b1
