重心の理解と活用

重心位置の求め方は、先人によってすでに各形状ごとに公式として示されています。ですから、まずは基本形状の重心位置のおさらいから始めましょう。

まずは、三角形の重心位置はどこかわかりますか？　（下イラストのように薄板の場合は重心というより、どちらかというと図心とい表現が適しているかもしれません。）

重心（図心）　三角形

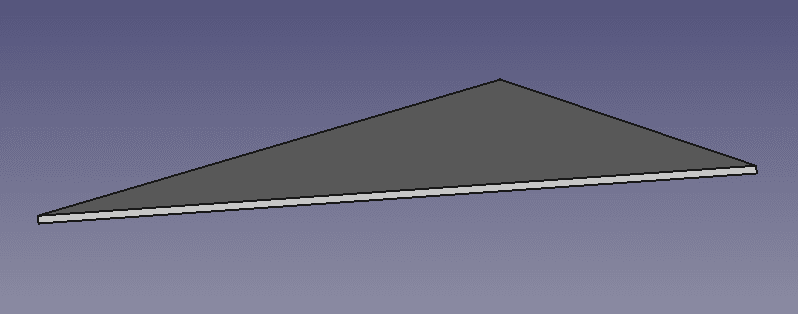
つぎに、薄板の円盤からさらに円盤を切り抜いたような形状になります。こうなるとちょっと難易度が上がりますね。このようなケースでは釣り合いという考え方が必要になりますよね。

重心（図心）　切り抜き円形

次は、立体形の重心位置はどうでしょうか。下イラストは円錐形状を真横から見ています。なんとなくどのあたりかは想像つくと思いますが、このような基本形状に関しては先人により導かれた重心位置を求める公式がありますので便利です。

重心　円錐

下イラストは球を半分にしたものです。これも基本形状なので重心位置を求める公式があります。

重心　半球

つぎは、二つの異なる形状の立体を繋ぎ合わせたものです。実際にはもっと複雑な形状のもが多いのですが、このようなシンプルな形状であってもちょっと難易度があがりますね。ここでも釣り合いの考え方が必要になります。

重心　複合立体形

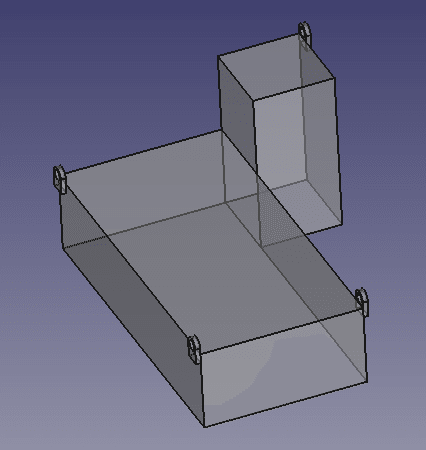
そして、このnoteは実際の作業現場において重心位置を理解した対応が出来るための資料となることを目的としています。