入試数学における点数の取り方②

どもども　まさかの②です。
今回は数学苦手な人向けと言うか部分点でもむしり取りたい人向けの記事となります。
前みたいに実際に入試問題を使ってやっていくので効果的ではあると思います
早速やっていきましょう！

本日やるのは〜〜〜〜〜？？？？？？？

2023東北大本レ〜〜〜〜！！！！！

問題を見た感じ　立体なので図示しにくい
(1)は計算ゲーぽいですね　図は書く必要無いと思います
(2)(3)は図書いてもいいですが立体なのでうーん　計算でどうにか…
って感じですね
ではやっていきましょう！

(1)を考えていきます。早速この記事で使用する考え方を使います。
その名も　逆算的考え　！！

当たり前ちゃ当たり前ですがどうやったらkが出てくるかを考えます。
問題文に与えられてる二つの式がヒントになりますね。ということです逆算的に考えるとこの式からkが得られると考えます。

この式を使用するにあたってどう使用するのかパート1でやったみたいに実験してみます。
そうすると問題文の半径1が鍵となっており最初の式に文字をかけても支障はないという事がわかりましたが問題文には載ってない掛け算が出てきてしまったので未知数が出てきました。
未知数を解決するためには連立方程式を立てないといけません　連立したら未知数がわかってkもきっと出てくるでしょう………
と逆算的考え方で方針を立てます。

この方針でやってみるとうまくkが出せました。

連立方程式を立てようとしましたがすぐkが出てきてしまいました。
せっかくなのでa,b,cの値を連立方程式で出してみましょう

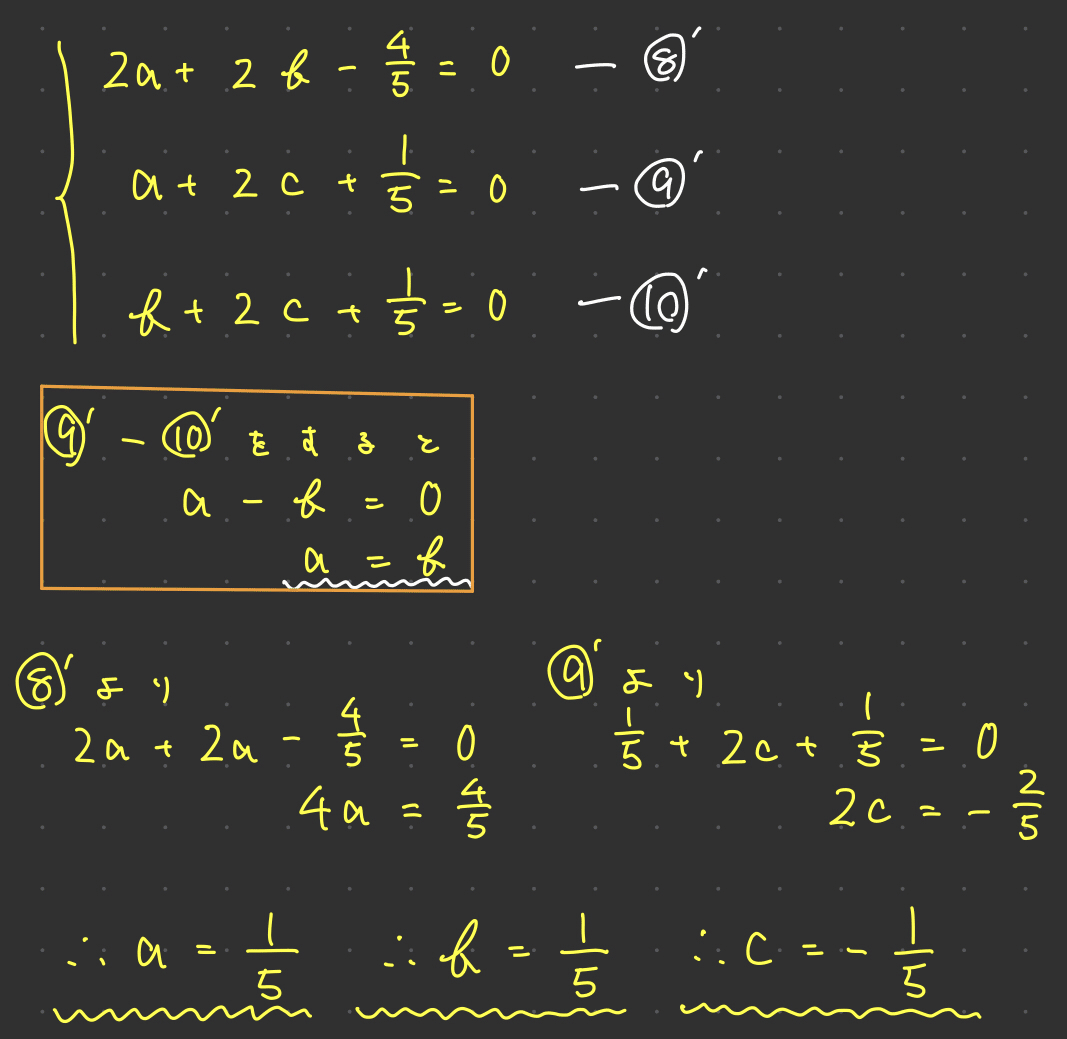
a=b=-cという値を得ました。きっと(2),(3)で使っていけるでしょう！(フラグ)

では(2)を考えていきましょう！
三角形ABCの面積を求めろということなので逆算的に考えると面積の公式を使うことになるでしょう。

ベクトル問題で三角形の面積といえばこの公式ですね

ということで逆算的に考えればこれを使えば答えが出ますね！
次にこの公式を使う為には
AB・ACとAの角度が分かれば公式が使えます。

AB・ACから求めていきたいのですがどうしましょうか？
ABとACをベクトルで考えてみると

①

このようになります絶対値は長さを表してますよね
2乗する理由は(1)でOA~ODで数値を出したので値が出ると思ったからです。

次はsinBACを出したいんですがベクトルの公式類を思い出すと内積の公式が有名ですよね！ですがそれはcosなのでsinをcosにする必要があります

②

ということで画像の通りになります。①ではAB,ACが必要でしたが②ではBCも必要ですね！！でも①と同様にすれば求められそうなので

結論はこうなります！！逆算的に考えるとこれを求めれば答えが出ることになります！
ということで解答です

やはり逆算的に考えることで入試数学における点数の取り方①のように簡単な問題文を書き直す事ができ、今自分がすべきことがわかりやすくなります

逆算的考え方のまとめです

言っちゃえば当たり前のことですが大事な考え方であってこれは数学だけで無く物理でも活用できると思います。仕事を求めるとなると公式で考えれば運動エネルギーが欲しいことがわかります！！なので物理でも十分この考え方ができます

ちなみに(3)は説明が難しかったのでそこの読んでるキミ！
挑戦してみてくれ！！