
FP1級 2023年9月試験 応用編第2問
おはようございます。🐤
昨日に引き続き応用編の感想と解説をいってみたいと思います。
第2問(金融資産運用)
C分野の応用編は、財務データのあれこれでした。
一般社団法人金融財政事情研究会 ファイナンシャル・プランニング技能検定 1級学科試験より
[問54]
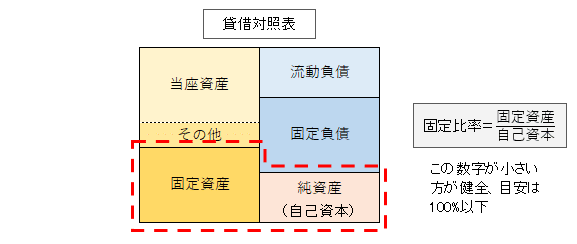
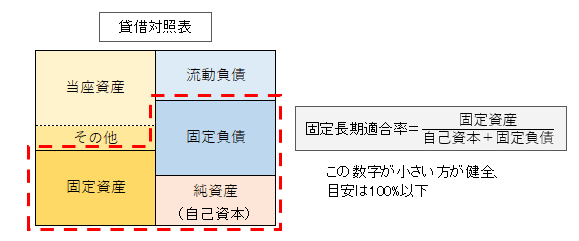
固定比率、固定長期適合率
固定比率、固定長期適合率はこの図ですね。
固定長期適合率、ああ、私の得意なの、もちろん私はマスターしています。ブログを書いたくらいだから絶対に自信あり、プレゼント問題ありがとう!
と思ったら間違えましたよ。きっちりとひっかかりました!わはは!(やけくそ)

自己資本は「純資産-(新株予約権、非支配株主持分)」で計算しないといけません。私はがっつりこれにはまってしまいました。この絵にやられた。自分の絵にやられた。
……いま気づいたけど、この絵で覚えていて私と同様にひっかかった人いますか? もしいたら本当に申し訳ありません。平謝りです。
というわけで答えは、
・自己資本=純資産-非支配株主持分=254-16=238
・固定長期適合率=固定資産/(自己資本+固定負債)
=110/(238+17)=43.14%
インタレスト・カバレッジ・レシオ
これは間違えなかったでしょうか。
値が大きすぎて少し不安にはなりましたが、事業利益/支払利息で、事業利益=営業利益+受取利息+受取配当金ですね。
為替差益をもしかして足しちゃった人いるかも。初見ですよね。このへんの嗅覚というか類推力というかが重要なのかも。私はたまたまだけど。
負債比率
はじめましてですよね、テキストには載っていませんよ。常識として知っているか仕事でよく使っているか、もしくは推理力を働かせます。
負債の比率だから、きっと分子は負債だ。でも何に対する比率なんだろう。わからん。というわけでネットに頼ると、自己資本に対する負債の率だということがわかりました。
というわけで 負債/自己資本=66/238=27.73%
これも純資産じゃなくて自己資本を使っています。だからもちろん芋づるで私はここもミスっているわけです。わはは。(やけくそ)
読み進めると、「負債比率が高いほど、④財務レバレッジが大きくなります」という文章があります。さっきはわからんと言いましたけど、財務レバレッジは総資産/自己資本なので、なんとなくここで負債比率は何に対する比率なのか推理できそうですよね、しかも「自己資本(純資産じゃなく)」という大ヒントも出ている。悔しい!
[問55]
標準偏差となんとかレシオ、そしてベンチマーク
比較対象となるのは①ベンチマークですね。ベンチマークって何かわかりますか? 基準点です。基準点って何かわかりますか?

国土地理院という役所みたいなところが、全国各地に置いている測量に使う基礎です。ここを基準にしていろいろなところの高さや距離を測ります。
だいたい大きさは4cm~5cmくらいかな、こんなに小さいけど絶対に動きません。なぜなら地盤の良さそうなところを選んで、その地盤を乱さないように1回だけ穴を掘って、そこを思いっきり念入りに地固めした上にしっかり砂利を荒さを変えながら何重にもひいて絶対に沈まないようにして、そこの上に大きなコンクリートの基礎を作ってまわりを土で固めて、絶対に動かないとわかってから、そこに基準点を埋め込むからです。絶対に動きません。ちょっとやそっとのいたずらでは絶対に動きませんが、間違って動かしてしまったらたぶん逮捕です。(知らんけど)
FP試験に戻って、ベンチマークとは例えば日経平均とかNYダウとか市場の動きの基準となる指数のことです。やたら動きますね。
ベンチマークと自分のポートフォリオとの離れ具合の一つ一つを合計して数値(標準偏差)で表したものをトラッキングエラーと言います。
なぜ「エラー」っていうかは、「ベンチマークを目指しているのに、そこから外れてしまったから」エラーって言います。
上振れの超過収益はエラーじゃないよねとか思ってしまうんですが、ベンチマークを目指しているんだから、そこから上にぶれても下にぶれてもエラーなんです。ベンチマークとエラーはセットです。
そして、その超過収益率をトラッキングエラーで割ったものを「インフォメーション・レシオ」といいます。
これは何かと似てますよね。FP1級受験生なら馴染みのある「シャープ・レシオ」です。シャープレシオは、ポートフォリオの収益率から安全資産利子率を差し引いて、それをポートフォリオの標準偏差で割ったものです。似てますよね。似てます。

何が似てるって、シャープレシオはポートフォリオの収益率から、安全資産=国債の利率を引いているんです。そしてそれを「標準偏差」で割る。
シャープレシオは標準偏差で割るんですけど、これは平均からのぶれ具合を表します。このぶれはエラーと呼ばないです。だって別に平均を目指しているわけじゃないから。
標準偏差っていうのは、「バラツキ」を数字で表したもので、この標準偏差が大きいと安定してないってことなんですね。例えば投資信託Aという商品の収益率が5%、標準偏差が1%だとすると、投資の結果はだいたい68%くらいが5%±1%、つまり4%から6%の間に収まるんです。

仮に標準偏差がもっと大きくて、例えば10%だとするとその結果は-5%から+15%の間までぶれるんです。標準偏差はプラスマイナスのぶれだというイメージで感じてください。覚えるのではなく感じるのが素敵です。

じゃあその標準偏差はどうやって求めるのかというと、これはとにかく実績をとります。理屈とか数式ではなくて結果を使って、ばらつきを求めて、一定のルールにあてはめてそのばらつき具合をひとつの数字で表します。

例えばこんな感じの投資成績のばらつき具合の投資信託Bがあったとします。こんな変な分布でも標準偏差は機械的に求めることができます。手順1としてはまず平均を出します。

そしてそこからのぶれをそれぞれの回ごとに計ります。ただ、ここでそのまま足し合わせると、平均からのプラスマイナスが打ち消されてゼロになってしまいますので、ぶれの2乗を計るのがコツです。
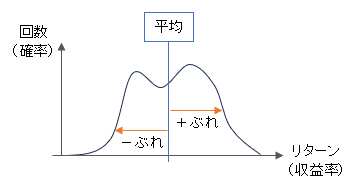
ぶれの2乗をすべて足すと、2乗なのでわけのわからない大きな数になってしまうので、それをルートで戻します。ちなみにこの2乗の数を足し合わせたものを「分散」と呼んで、それにルートをかぶせたものを「標準偏差」といいます。でてきましたね、標準偏差。
ちなみにこんな図のような不格好な分布だと、標準偏差の中に68%が収まるとは限りません。68%が収まるのは左右対称できれいな分布の時だけです。
トラッキング・エラーもすごく似ていて、しかし「平均からのぶれ」ではなくて「ベンチマークからのぶれ」を使います。ベンチマークからのぶれを2乗して、それを足し合わせたものにルートをします。つまり、トラッキング・エラーの正体はベンチマークからのぶれの標準偏差なのです。
平均からのぶれ=標準偏差
ベンチマークからのぶれ=トラッキング・エラー(という名の標準偏差)

な、長い…ここまで読めた人いますか? まだ誰か残っていますか?

残ってくれた人にはプレゼントで、トラッキングエラーとインフォメーション・レシオを結びつけるこんな図をどうぞ。
ところで、もう少しインフォメーション・レシオについて考えてみると、インデックス系の投資信託が目指すのはベンチマークそのものですよね。なのでトラッキングエラー=分母がゼロに近づくので、インフォメーションレシオはほぼ役に立ちません。
インフォメーションレシオが役に立つのは、アクティブ系の投資信託です。
ベンチマークからの上ぶれが大きいと分子は大きくなります。一方でぶれが大きいから分母のトラッキングエラーも大きくなります。
分子はぶれ、分母はぶれの2乗のルートです。同じようですが、ぶれが常に一定であるほど分母は小さくなります。つまり、上ぶれが常に一定だとインフォメーションレシオは大きくなります。
仮に上ぶれが一定だと、インフォメーションレシオの最大値は1です。しかし、今年だけ特に上ぶれが大きかったら、今年に限り1よりも大きくなります。来年度もし同じ収益率を上げられたとしても、1より大きくはなりません。
ということはインフォメーションレシオは何の参考になるのでしょう?
とにかく大きければいいというわけでもなさそうですが、インフォメーションレシオを参考にしてやろうと思っても、例えばヤフーファイナンスやSBI証券にはインフォメーションレシオは掲載されていません。
つまりこれは試験のための知識です。シャープレシオはよく使うんですけどね。
それでは試験に戻って続けます。
金額加重収益率、時間加重収益率
⑤金額加重収益率というのは初見ですね。
この収益率はポートフォリオへの資金の流出や流入を含めたものだそうです。初見ですね。試験問題中にでてきた□□□加重収益率はおそらく「時間収益率」というもののようです。
時間加重収益率はもしかしたら計算問題が得意な人は知っているかもしれません。1年目に10%、2年目に12.5%だったときの平均は、というような感じの問題がありましたよね。

なんなんだよと、途中で引き出すなよややこしいと言いたくなるこんな問題ありましたよね。見覚えないですか?
この問題のコツは、1期目の年利率と2期目の年利率をまず計算して、それからその率で1期目から100万円とかわかりやすいキリの良い数を運用したらそれが答えになります。2023年1月の問題の場合は、1期目20%、二期目-20%なので、100万円⇒120万円⇒96万円になります。
ここわかりますかね?
第1ステップ、期ごとの利率を求める
・利率=利益/投資額
・1期目 (120-100)/100=20%の利益
・2期目 (80-100)/100=-20%の利益
第2ステップ、最初から一定額を運用する、例えば100万円。
・1期目 100万円×1.2=120万円
・2期目 120万円×0.8=96万円
で、結論として2年で100万円が96万円になったということですから、1年あたりの利率をyとすると、100×(1+y)^2=96になるんです。なんかここ難しいですよね。÷2でいいじゃんと思うんですけど、複利計算なので2乗になります。
というわけで(1+y)^2=96/100
(1+y)=√0.96=0.97979…
y=0.97979-1=0.02020…
という…私説明下手ですね。
試験問題に戻って、1年目に10%、2年目に12.5%だったら、仮に100万円をずっと運用したとすると
・1年目 100万円⇒100万円×110%=110万円
・2年目 110万円⇒110万円×112.5%=123.75万円
つまり、100万円が2年で123.75万円になったということですから、1年あたりの利率の2乗が1.2375倍ということで、それにルートをかぶせた√1.2375=1.1124。利率になおすと11.24%が正解になります。
私ほんとに説明下手だな、こんなんでわかりますか?
しつこく時間加重収益率
逆に、年利が11.24%の投資商品があって、その利率は安定していて、1年目も2年目も11.24%だとします。
・1年目 100万円⇒100万円×111.24%=111.24万円
・2年目 111.24万円⇒×111.24%=123.743376万円
ほら、だいたい123.75万円になったでしょ。
これが、10%と12.5%の平均だから、足して2で割って11.25%、とか考えそうになるんですけど、これで2年運用すると、
・100万円×1.125=112.5万円
・112.5万円×1.125=126.56万円
これは明らかに123.75万円じゃないですよね。だから単純な平均ではなく、「時間加重収益率」を使うのが正しいのです。
さっきの、1年目10%で2年目12.5%だった時と同じ。100%とか1を引いたり足したりの感覚が難しいかもしれないですね。私はそのへん説明してないですから。
利率が10%の時に100万円を1年間運用したら110万円になるのって、実は2つの計算を一発でやるという複合技をしているのであって、100万円×10%=10万円+元本100万円=110万円ということをやっているんですね。それを私は一発で110%とかしちゃうからややこしいのかも。
複利の計算はややこしいですね。なんとなくでもついてきていただけたら嬉しいです。もし難しかったら私の説明が悪いので安心?してください。
[問56]
ここは過去問にたくさんあるから大丈夫でしょうか。覚えるのがたいへんですね。
相関係数=共分散/(標準偏差×標準偏差)
ポートフォリオの標準偏差=(Xの比率×Xの標準偏差)^2+(Yの比率×Yの標準偏差)^2+2×(Xの比率×Yの比率×共分散)
下の式は(a+b)^2=a^2+b^2+2abというのがわかる人はそのイメージで、わからない人はひたすら暗記で、よろです。
まとめ
なんか今回はめちゃくちゃ独りよがりで不親切だった気がします。質問ばんばん受け付けますので、もし良かったら質問していただけたらすごくありがたいです。その質問によってブログ修正できたら私が嬉しいです。
というわけで眠いので寝ます。
それではまた、FP~(@^^)/~~~
