数理最適化入門

最適化について自分が勉強した内容を書いていきたいと思います。
手書きの図とかが入っています。変な言い回しをしているかもしれません。
温かい目で見てあげてください。

数理最適化

数理最適化とは

与えられた制約条件内で目的関数の値を最小(or 最大)にする解を求めること

例えば，お酒だけで１日の栄養を補う必要があるときがあったとします。そのときのお酒の購入料金を最小化したいです（これを最適化問題の内の１つ，最小化問題といいます）。
最初に，下のような情報を使って定式化して，最適化します。
（本当はもっとお酒の種類もあるし，栄養のバランスも必要量も料金も適当です。良い意味でいうと架空のものです。）

現実問題

上の情報を下のように定式化することで，数理最適化を行うことができます。
栄養の必要量を制約条件として，この条件を超えるよう（不等式の関係で超える・超えないは変わります）にお酒の量を決めます。この条件の下，お酒の購入料金を最小化していきます。
これが数理最適化による最適化問題です。

現実問題を定式化

※これはただの例なので，良い子はお酒だけで栄養を補わないようにしてください。多分息絶えます。

数理最適化の流れ

数理最適化を実務で使うときなどの流れを説明していきます。
下には図で表してるものもあります。

1. 現実の問題を見つける

2. 最適化問題の定式化（現実の問題を数理モデルにする）

3. 最適化問題をアルゴリズムにより救解

4. 計算結果の分析・検証

5. 最適化問題とアルゴリズムの再検討（３,４の繰り返し）

6. 良いのが出たら終わり！
   

最適化の流れ

最適化問題

最適化問題を一般的に表すと，

$$
最小化　　f(x)\\
  条件  　　x \isin S
$$

となる。
$${x \isin S}$$は，変数：$${x}$$は，集合(実行可能領域)：$${S}$$に属するといいます。
難しい言い方をしてますけど，$${S}$$の中に$${x}$$がありますよ～的なニュアンスです。
最適化の一般式を見ただけでは，なんのこっちゃなんで
図で表すとわかりやすいかと思います。

最適値・最適解・実行可能領域

実行可能領域：$${S}$$の中で，変数：$${x}$$を変化させていって，目的関数：$${f(x)}$$が最小値（最大化問題なら最大値）になる値が最適値：$${f(x^{*})}$$となります。
$${f(x^{*})}$$のときの変数：$${x}$$を，最適解：$${x^{*}}$$といいます。
最適値や最適解の$${x}$$に付いてる $${*}$$ は「スター」と読みます。数理最適化では元の値と最適後の値を区別するために使用しています。

一般的に最適解は１つのみ。最適化問題を解くということは，「最適解を１つ求める」ということになる。
しかし，最適解は複数存在する可能性があり，全ての最適解を求めることは，列挙問題とされています。

用語の説明

数理最適化・最適化問題に関する用語の説明です。関係ある本やネットの記事を読むのに用語を知らないと全然読めないので知っておいて損はないかと。

• 数理モデル：現実の事柄を数式にして表す
  「年齢が上がると年収が上がる」を$${y = ax+b}$$みたいに表すこと

• 最適化問題：定数，変数，制約条件，目的関数から作られている

• $${x}$$：変数，決定変数

• 解：変数の値

• 実行可能解：制約条件を満たす解

• 実行可能領域：集合$${S}$$

• 制約付き最適化問題：制約条件のある最適化問題

• 制約なし最適化問題：制約条件のない最適化問題

• 目的関数：関数$${f}$$

• 最小化問題：目的関数が最小になる実行可能解を求める

• 最大化問題：目的関数が最小になる実行可能解を求める

• 最適解：最適化問題で求めたいのもの（目的関数$${f(x)}$$の値）最小化問題であれば最小の値・最大化問題であれば最大の値

• 最適値：最適解のときの目的関数$${f(x)}$$の$${f(x)}$$の値

最適化問題の解の分類

最適化問題の解の分類は，主に４つあります

• 実行不能

  • 制約条件を満たす解が存在しない。

• 非有界

  • 目的関数が無限に更新できてしまい，最適解が存在しない。

• 有界であるが最適解が存在しない

  • 目的関数は有限であるが，最適解が存在しない。

• 最適解が存在する

  • 有限な最適解と最適値が存在する。

非有界と有界であるが最適解が存在しないをわかりやすいように図に表します。

例1）最大化問題の「非有界」

非有界

制約条件に目的関数がひっかからず，目的関数の値がどこまでも大きくなってしまうため，最適解が存在しません。

例2）最小化問題の「有界であるが最適解が存在しない」

有界であるが最適解が存在しない

目的関数を小さくしていくと値が$${0}$$に落ち着きます。しかし，$${0}$$となる実行可能解は存在しないため，最適解無しとなります。

大域最適解と局所最適解

極値がたくさんあると，本来求めたい１つの最適解（大域最適解）まで学習が進まず，小さい範囲での最適解（局所最適解）に捕まってしまうことがあります。

• 大域最適解（本来はこっちを求めたい）

  • 実行可能領域内での最適解

• 局所最適化

  • 実行可能領域内の近傍内での最適解

大域最適解・局所最適解

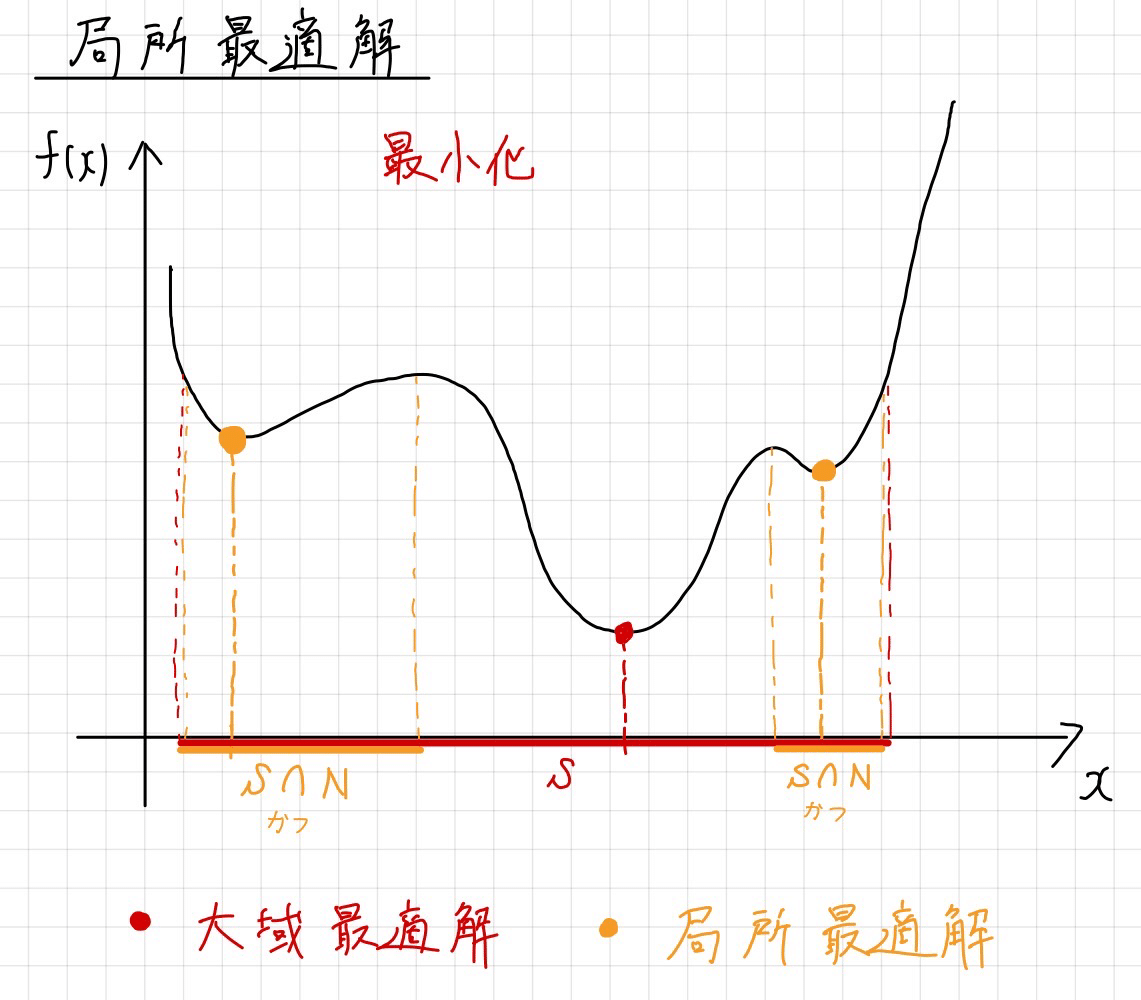
本来求めたいのは全体の最適解（赤い範囲）ですが，この図では最適化中に局所的な範囲（オレンジの範囲）で捕まってしまいます。そのため，局所最適解しか導けず，本当の最適解（大域最適解）を導けません。
この図の$${N}$$は近傍といいます。$${S}$$かつ$${N}$$で局所的な範囲を表しています。

代表的な最適化問題

最適化問題は，連続最適化問題と離散最適化問題に大きく２つに分かれています。ここでは，最適化問題の種類について説明していきます。

連続最適化問題

変数が実数値のような連続的な値（無限に切れる）をとる問題を連続最適化問題といい，実数値をとる変数を実数変数をいいます。

• 線形計画問題（LP）

  • 目的関数，制約条件（等式or不等式）が共に線形関係のもの

• 非線形計画問題（NLP）

  • 非線形な目的関数，制約条件（等式or不等式）が含まれているもの

• 2次線形計画問題（QP）

  • 目的関数が2次関数，制約条件（等式or不等式）が全て非線形関係のもの

離散最適化問題【組合せ最適化問題】

変数に整数値や2値｛0, 1｝のような離散的な値の最適化問題。
解の集合が順列やネットワーク構造などの組合せ的構造がある最適化問題もこれにあたる。
整数値のみの変数を整数変数，2値｛0, 1｝のみの変数を2値変数といいます。

• 整数最適化問題（IP）

  • 全ての変数が整数のもの

• 混合最適化問題（MIP）

  • 1部の変数が整数のもの

• 2値整数計画問題（or　0-1整数計画問題）

  • 全ての変数が2値のもの

• ネットワーク最適化問題

  • ネットワークやグラフの構造で表せるもの

結構細かく分かれていましたが，本来はもっと細かく分かれていて全て覚えるのかなり大変だと思います。覚えたい人は要努力が必要ですでね～。

終わり

とりあえず，入門としてはしてはこれで終わります！
最後まで見ていただき，ありがとうございました！