
macOSで数式を計算する (2)
前回の導入編では、数式を計算するために、Jupyterlab, Sympy, LaTeX などを導入した。今回は実際の計算である。
はじめの一歩
加算
まずは、簡単な数式からだ。a, b は何も指定しないと複素数と解釈されてしまうらしいので、整数として定義する。加算(足し算)は整数は順序を変えても答えは変わらない。交換法則というのを覚えている方もいるかもしれない。(赤い線がついているのは、英語の文法チェッカーが働いてしまっているせいで、本題には、関係ない。)
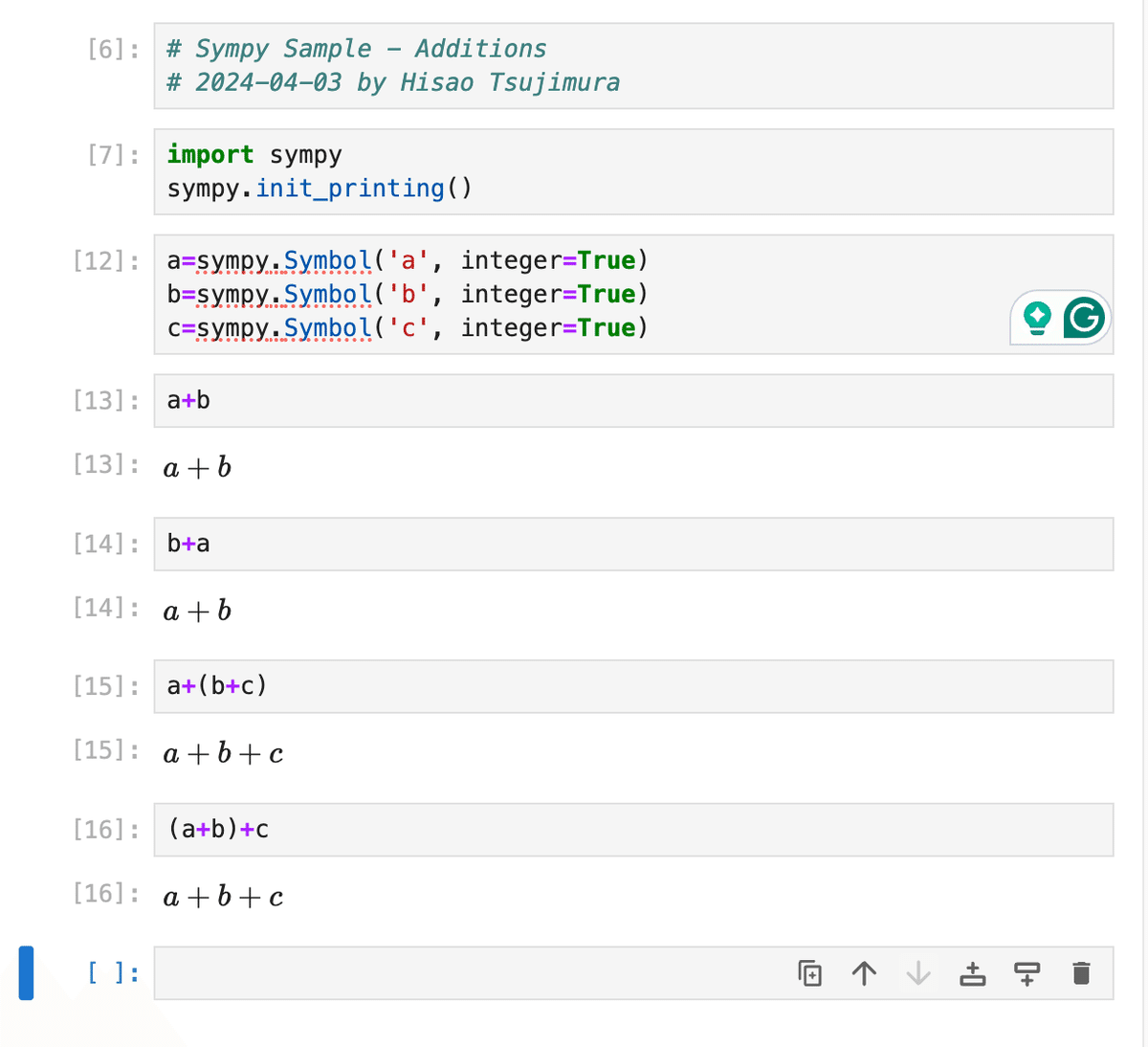
なお、Sympyでは、Integer=Trueのようなものを Assumption という。これには、「整数であれば、こういう性質のはず」という属性が含まれているので、「順序を交換できない(可換でない)整数」などという妙なものを定義すると、ちゃんとエラーが出る。
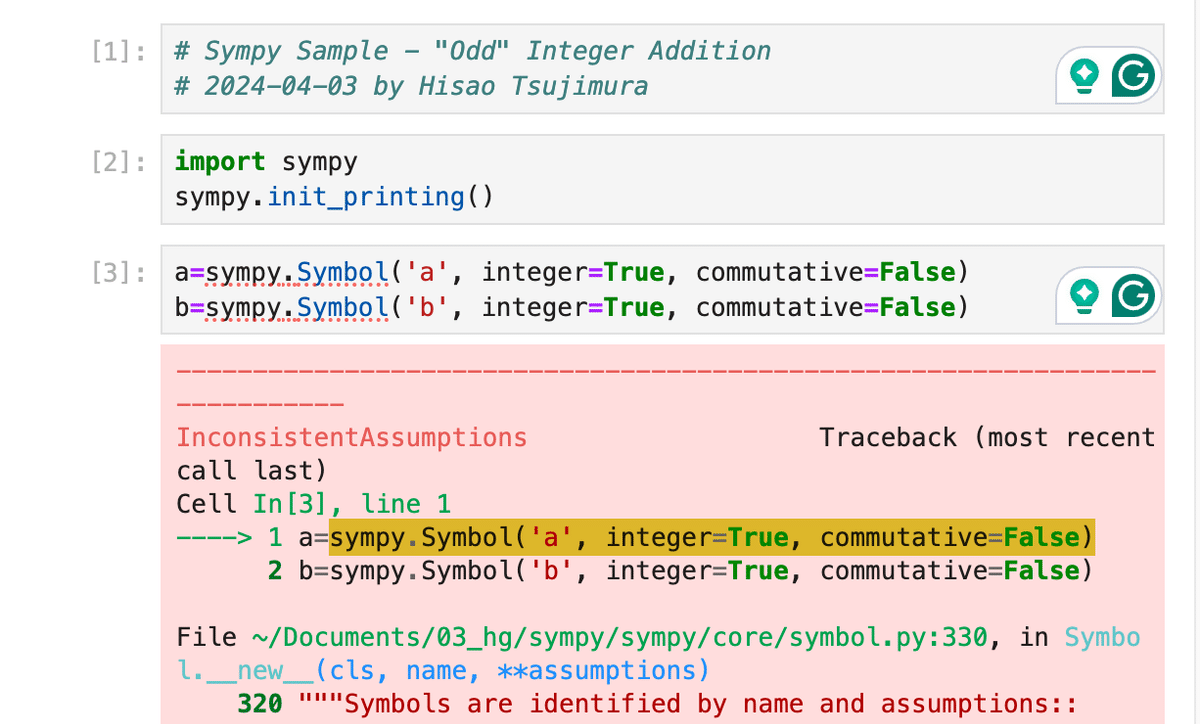
減算
つづいて、減算、つまり引き算だ。
(なお、変換の一発目が星野「源さん」だったのは内緒である。)
引き算は一見順序を変えると答えが変わってしまうように見える。
実はそうではなくて、a-bと b-a は行っている計算が異なる。それぞれ、a+(-b)、b+(-a) である。以下の例の最後を見ると分かるが、b+(-a) と (-a)+b は順序を変えても同じである。[^1][^3]

加算に直すと異なる値の計算をしているのがわかる
何かと話題の乗算
かけ算の順序問題
「かけ算の順序問題」というのが時折 SNS を賑わせてる。
乱暴に要約するなら、文章題などで、A × B = C が正解であるとき、B × A = C は誤りであるとするものである。
著名な数学者の方もコメントしているこの問題、私が何かを語るなんておこがましいので、Sympy に計算してもらうとしよう。整数は乗法についても可換であり、順序を変えることができる。また、結合法則も成り立つ。[^2]

順序を変えてはいけないかけ算
一方、順序を変えてはいけないかけ算という物も存在する。
一例が行列である。なお、サンプルコードは、Python (SymPy) による行列の計算 のコードを引用させて頂いた。

少し分かりづらいが、A × B と B × A の結果は異なる。
Sympyって何がうれしいの?
個人的には数式を解いてもらえるところだ。

コメント
[^1]: 整数の全体 Z はアーベル群なので、加算について順序は問わない。ただ、私たちの思う「引き算」は、a や b の逆元を加算している。この例では、マイナスの値(逆元)として加算している変数が各々の式で異なる。
[^2]: アーベル群は乗法についても可換である。
[^3]: コメントをいただいたので付記しておく。この記事では「整数の減算」を「逆数を加算する」として紹介している。正のの整数の逆元がマイナスの整数であることが前提であって、群の台集合として正の整数「のみ」を考える場合はこの話は成り立たず、また、a - b で a < b の演算もできなくなる。
参考文献
ご参考
今回および導入編で使ったサンプルコードは以下に公開してある。
いいなと思ったら応援しよう!

