微小な変数をcurve_fitで決める時の注意事項

pythonの勉強をしててハマった罠について、自分への備忘録を兼ねてここに記録しておく。
今回フィッティングしようとしたのは以下の図のような状況についてである

RC回路と、抵抗の電圧値の時間変化

電源に接続された抵抗とコンデンサーという標準的なRC回路について考える。Sはスイッチである。ここで抵抗Rは$${50\Omega}$$であり、$${t<0}$$で極板は完全に放電しているものとし、$${t=0}$$でスイッチをオンにする。電源電圧は常に一定にする。この状態でスイッチをオンにした後の抵抗の電圧値が表1である。この時pythonを使ってグラフにフィッティングし、Cの値を推定してみよう。
このRC回路における抵抗の電圧の変化は以下のような式で表記される。

$$
V_R = V_0\exp(\frac{-t}{RC})
$$

この曲線にフィッティングさせる時に使えるpythonのツールがscipy.optimize.curve_fitである。

使い方は至って簡単である
まずは必要なパッケージをimportしておく。

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit

そしてデータを次のようにarray型で用意しておく。

time = np.linspace(0, 0.18, 10)
resis_voltage = np.array([4.9, 3.3, 2.3, 1.5, 1.0, 0.66, 0.46, 0.29, 0.21, 0.14])

そしてフィッティングしたい関数を定義する。

def funcV_R(t, C, V_0):
    return V_0 * np.exp(-t / (50*C))

基本的にはここまでで準備は完了で、フィッティングは次のように実行する。

popt, pcov = curve_fit(funcV_R, time, resis_voltage)

これでpoptに変数の最確値が格納され、pcovに共分散が格納される。
さて、これでうまくいったかなーと思い以下のようにグラフにプロットさせてみる。

plt.plot(time, resis_voltage, "b.", label="raw deta")
plt.plot(time, funcV_R(fit_time, *popt), "r-", label=f"fit:R=50,C={popt[0]:.2f},V_0=[popt[1].2f")
plt.xlabel(r'$t(ms)$')
plt.ylabel(r'$V_R(V)$')
plt.legend()
plt.xlim(0, 0.18)
plt.grid()
plt.show()

最初の二行で値をプロットし、次の二行で軸のラベルを追加し、legendで凡例を表示させ、xlimで見やすいようx軸の範囲を固定、gridでグリッド線を追加する。
これを実行してみると以下のようになる。

first try

どうもフィッティングがうまくいっていないようである。一般的にcurve_fitでフィッティングがうまくいかない原因として筆者が調べて見つかった要因は以下の通りである。

• フィットする関数が多価関数になっている

• パラメータ空間に鞍点が複数ある

これらの問題はcurve_fitがあくまであくまで最小2乗法で計算しているからである。一つ目は明らかに問題ないので、二つ目の可能性を考えて初期値を調整すると実はうまくいった。が、一般性を欠いていてあまり綺麗なコードではない。ちなみに初期値は以下のようにして設定できる。

initial_guess = [5, 0.01]  # 初期推定値を設定
popt, pcov = curve_fit(func, time, resistance_voltage, p0=initial_guess)

非常に天下り的で好きじゃないのだが、手で計算して推定した値を代入している。すると以下のようにうまくいった。

second try

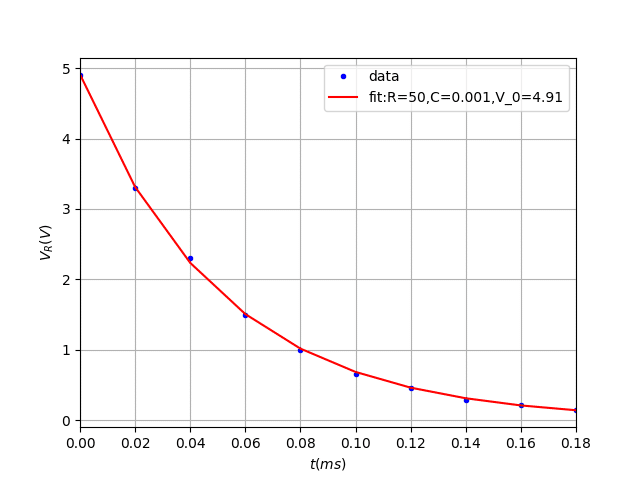
こんなやり方は一般性も何もないが、なぜうまくいかないことがあるのかというと、Rの大きさに対してCの大きさはオーダーが四桁も違うことに起因すると考えられる。expの肩に乗った数字の分母が0に近い値で初めてうまくフィットするとなると、curve_fitの初期値はデフォルトで1なのでうまくいかなくなるらしい。Rの値をあえて決めずに行うと実はこれもうまくいく。RもCも$${10^{-1}}$$のオーダーで値を持つから計算ができるのだ。

def func(t, R, C, V_0):
    return V_0 * np.exp(-t / (R*C))

popt, pcov = curve_fit(func, time, resistance_voltage)

third try

RとCの値は別々に出たが、RCの大きさがわかるのでCが計算できるという感じだ。これも一つの解決策だろう。要するに分母に決めたいパラメータがあって、その値が十分小さいオーダーだとcurve_fitではうまくいかないことがあり得るのだ。これはよく注意しなくてはならない。物理の数値計算ではオーダーが異なるパラメータが入ってくるなどよくあることなので、注意して計算する必要がある。これらを考えると、欲しいパラメータが分母になければいいので1/Cをcurve_fitで計算させることにした。また、$${V_0}$$は流石に表1から明らかに4.9なので最初からそのように指定した。さらに、フィットさせた関数が滑らかに表示されるように調整した最終的な結果が以下のものである。

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit


# 今回使う関数を定義
def funcV_R(tt, CC):
    tt = np.array(tt)
    fracC = np.array(CC) / 50
    return 4.9 * np.exp(-tt * fracC)


# データを作成
time = np.linspace(0, 0.18, 10)
resis_voltage = np.array([4.9, 3.3, 2.3, 1.5, 1.0, 0.66, 0.46, 0.29, 0.21, 0.14])

# フィッティングの実行
popt, pcov = curve_fit(funcV_R, time, resis_voltage)

# フィッティング関数を滑らかにプロットするための変数列
fit_time = np.linspace(0, 0.18, 100)

# 実際の静電容量の値
C = 1 / popt[0]

# グラフのプロット
plt.plot(time, resis_voltage, "b.", label="raw deta")
plt.plot(fit_time, funcV_R(fit_time, popt[0]), "r-", label=f"fit:R=50,C={C:.4f},V_0=4.9")
plt.xlabel(r'$t(ms)$')
plt.ylabel(r'$V_R(V)$')
plt.legend()
plt.xlim(0, 0.18)
plt.grid()
plt.show()

fourth try