
基数変換をできるだけ難しい計算をせずに解きたい人へ(10進数→2進数→16進数)#2
はじめまして。hirokiと申します。
都内で情シスをしている30前半のどこにでもいる普通のエンジニアです。
今日はタイトル通り「基数変換をできるだけ難しい計算をせずに解く」の後編(10進数→2進数→16進数)を説明させて頂ければと思います。
できれば一つ前の記事から見ていただくと、話しの流れ的にわかりやすいかと思います。↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
10進数→2進数への変換
2進数→16進数への変換
10進数→16進数への変換
1. 10進数→2進数への変換
10進数から2進数に関しては変換表を使って一発で求めることができません。ですがこちらも簡単なルールに沿って足し算をしていくだけで求めることができます。前回と同様、まずは以下のような簡単な下準備をしてください。
① 箱を8つ書く。(本当は何個でもいいのですが、IPアドレス系の問題はこの数で十分なのでいったん8個にしています。)

② 一番左の箱の上に1を書く。

③ 右から左に一つ前の数字を2倍した値を箱の上に書いていく。

これで下準備は完了です。試しに例題をやってみましょう。
例題1)10進数「211」を2進数に置き換える
考え方の基本は箱の上に書いてある数字のうち、どれとどれを足していけば「211」になるか?ということになります。今回のように8つの箱を用意すると「128、64、32、16、8、4、2、1」という8つの数字を扱えることになります。不思議なことに、この8つの数字の足し算の仕方を変えて行くだけで、10進数の0~255という数字を表現できます。2進数はどの数字を使って足し算を行ったかを表してくれているという感じになります。(うまく伝えられなくてゴメンナサイ・・・)1回以下の計算を見ていただければ何となくイメージはつかめるかと思います。
①-1. 箱の上の数字(128)をそのまま箱の下に書いてください。

①-2 箱の下の数字(128)と比べたい数字(211)を比較して、箱の下の数字(128)のほうが小さかったら、箱の中に「1」を入れる。
箱の下の数字(128)< 比べたい数字(211)

②-1. 右隣の箱に移動をして、1つ前の箱の下の数字(128)と今の箱の上の数字(64)を足した数(128+64=192)を箱の下に書いてください。

②-2. 箱の下の数字(192)と比べたい数字(211)を比較して、箱の下の数字(192)のほうが小さかったら、箱の中に「1」を入れる。
箱の下の数字(192)< 比べたい数字(211)

③-1. 同じように右隣の箱に移動をして、1つ前の箱の下の数字(192)と今の箱の上の数字(32)を足した数(192+32=224)を箱の下に書いてください。

③-2. 箱の下の数字(224)と比べたい数字(211)を比較して、箱の下の数字(192)のほうが大きかったら、箱の中に「0」を入れる。
箱の下の数字(224)< 比べたい数字(211)
箱の中に0が入るときは、わかりやすいように箱の上の数字と足した数字に×印をつけて、1つ左隣の箱の下にある数字(192)をそのまま書いてください。
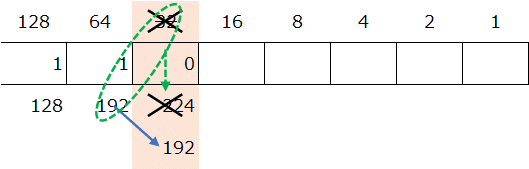
あとはこれの繰り返しを最後の箱までやっていきます。

一番右まで行ったら、OKです。
今回は「11010011」が答えになります。

最後に検算として、箱の上にあるバツがついていない数字を全部足してみましょう。

この数字が設問と同じになっていたらOKです!
これが最初に言っていた、
「128、64、32、16、8、4、2、1」という8つの数字を扱えることになります。不思議なことに、この8つの数字の足し算の仕方を変えて行くだけで、10進数の0~255という数字を表現できます。
という部分に繋がっていきます。
(うまく伝えられた自信がちょっとないですが・・・笑)
2. 2進数→16進数への変換
2進数から16進数の変換は簡単です。一つ前の記事で以下のように書きました。
16進数は2進数4桁で表現できる特徴があります。これはとても重要です!
この特徴に沿って16進数で表現されている文字を2進数の4桁に置き換えていけばOKです。
ですので・・・
2進数4桁は16進数1文字で表現できる特徴があります。
この特徴に沿って2進数で表現されている文字を4桁ごとに16進数1文字に置き換えていけばOKです。
ということになります。
前回と同様、下準備として試験の時は何も難しいことを考えずに下の表を空いてるスペースに書き込んでしまいましょう。これだけで準備完了です。

せっかくなので1つ前で求めた計算結果の続きで例題を考えていきましょう。
例題2-1)2進数「11010011」を16進数に置き換える
まずは2進数「11010011」右から4桁ごとに区切ってください。
【※※注意※※】左から区切ったらダメです!必ず右から区切ってください!

上記の対応表を見ると2進数「1101」は16進数「D」、2進数「0011」は16進数「3」であることがわかります。
あとはこれを順番にくっつけて「D3」が答えになります。

試しにもう一問やってみましょう。
例題2-2)2進数「101110」を16進数に置き換える
1つ前の例題と同じように、2進数「101110」右から4桁ごとに区切ってください。
【※※注意※※】左から区切ったらダメです!必ず右から区切ってください!

2進数の桁数によっては一番左の箱の数字が4桁にならない場合があります。その場合は前ゼロを付けてあげて4桁になるように補正をしてあげてください。

あとの手順は同じで、対応表からマッチする16進数の値を見つけてあげて答えてください。今回の場合は16進数「2E」が答えになります。
3. 10進数→16進数への変換
こちらに関しては前記事にも書きましたが、10進数から16進数はテキストに書いてあるような小難しい計算をしたら一発で出せますが、慣れてくるまでは10進数を一度2進数に変換し、その2進数を16進数に変換するやり方がおすすめです。(今回の場合ですと例題1→例題2-1の流れになります)
上記の1,2でやった方法で順番に変換を行えば簡単な掛け算と足し算だけで10進数→16進数の変換ができます。
本当にそうなるかは練習がてらに皆さんご自身で計算してみてください!
どうでしょうか。これなら何とかできそうな気がしませんか?
慣れてきたら自然と計算で求められるようになったり、数字を見ると大体頭の中で変換できるようになりますが、慣れるまではこのやり方で問題を解くのもありだと思います!参考になりそうだったらぜひ試してみてください!
今回自分の頭の中で理解していることを文字に起こしてみましたが、やっぱり人にわかりやすく伝えるために文章を書くのは難しいですね。

わからない部分があれば個別にお伝えすることも可能ですのでコメント欄に書いていただけると幸いです。
少しでもこのあたりを苦手に思っている人に役に立てれればうれしいです!
------------------
photo:いらすとや(焦って書類を書く人のイラスト(男性) | かわいいフリー素材集 いらすとや (irasutoya.com))
#IT #勉強法 #資格 #国家資格 #情報処理技術者試験 #基本情報技術者試験 #応用情報技術者試験 #基数変換 #n進数
