
機械学習でチャートをグループ分け
痩せた土に果実は実らない。
OUTPUTが貧困なのはINPUTが貧困だからである。
と思い立ち、最近、機械学習の勉強をしている。大学が無料公開している講義を聞いたりテキストを読んだり、Youtubeを見たり、書籍を読んだりしている。
学生でいる期間より社会に出てからの期間の方が圧倒的に時間は長い。こういうコツコツとした学びが人生を豊かにするのだ!(モテたいのだ!)
と、鼻息荒く勇み足で手をつけてみたものの
微分・積分・偏微分と面白くない。
難しいし、つまんないのである。圧倒的に眠いのである。Zzz...
なぜ、眠くなるのかと言うと、活用イメージが湧かないからである。(モテるイメージが湧かないからである。)
という事で、INPUTしながらOUTPUTする事にした。
なにやら、機械学習にはK-Means法というのがあって、似た要素でグループ分けができるようである。
そこで、クラスタリング機能(グループ分け)でチャートを分類し、似た銘柄を判別してみる事にした。
K-Means法で分類すると下図のようにグループ化された。
同じグループには「エネルギーセクターETF」や「XOM」や「CVX」などの石油系の企業が同じに分類されていていい感じである。
ここで、チャートが「ネギっぽい」感じなのには隠された理由がある。

分類の精度を上げるまでには紆余曲折があった。
似たチャートをグループ化を何度かやってみたのだけど、なかなか適切に分類されない。例えば9割が同じ形だと、最終日に暴落・暴騰していても同類と判定されるのだ。狙った分類をするにはチャートで重視したい特徴に重み付けをしてやる必要があるのだ。
類似性を見るのに軸メモリが邪魔なので、消そうとしたんだけど消えない部分があったので、バックグラウンドを黒にして塗りつぶした。机の上の散らかっているのが目立つ時は、部屋全体を散らかせ方式である。
次に、チャートの重要なポイントで類似性を判別させたいので、開始・終了付近の線を太い線(特に終了部分)にした。さらに最大値・最小値を目立つように白く大きなドットをつけた。
そして、メインの線を緑にすれば、ネギっぽいチャートが完成である。
(緑に深い理由はない。)
こうやって完成したのが、次のネギチャート仕分けのコーディングである。
仕様
・株価を取得。
・特徴を持たせたチャートを画像で出力。
・K-Means法にてクラスタリングし、画像をフォルダーに分類。
(20個のグループ(変更可能))
・フォルダに分けられた画像をグループ単位で並べて出力。
コーディングは以下の通り。
0.ライブラリインストール
pip install yfinancepip install japanize_matplotlib1.株価取得処理
import yfinance as yf
import pandas as pd
import numpy as np
import datetime
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline
# データ取得期間設定
start = datetime.date.today() - datetime.timedelta(days=40)
end = datetime.date.today()
payload=pd.read_html('https://en.wikipedia.org/wiki/List_of_S%26P_500_companies')
first_table = payload[0]
df500=first_table[['Symbol']]
tickers_tmp = df500.Symbol.values.tolist()
tickers = [item.replace('.', '-') for item in tickers_tmp]
tickers2=['^N225','BTC-USD','ETH-USD',
'VOOG','VOOV', 'SPYD','TQQQ','SPXL','SOXL','^GSPC','^DJI','^IXIC','SOXX',
'VIG','TLT',
'VTI','VOO','QQQ','^TNX','^RUT',
'VDE','VFH','VAW','VIS','IYR','VOX','VDC','VCR','VHT','VGT','VPU',
'VUG','VTV','VBK','VBR']
tickers_tmp2=np.append(tickers,tickers2)
tickers=tickers_tmp2.tolist()
# 株価データ取得
data_stock = pd.DataFrame(yf.download(tickers, start=start, end=end)['Adj Close'])
data_stock=(1+data_stock.pct_change()).cumprod()
data_stock.iloc[0,:]=1
# カラム名置換
data_stock.rename(columns={'VDE':'エネルギ','VFH':'金融','VAW':'素材','VIS':'資本財','TQQQ':'レバナス',
'IYR':'不動産','VOX':'通信','VDC':'生活必需','VCR':'一般消費',
'VHT':'ヘルス','VGT':'情報','VPU':'公共','^TNX':'金利10Y',
'^DJI':'Dow30','^IXIC':'NASDAQ','^GSPC':'S&P500','^RUT':'Rs2000',
'VBR':'小型 Val','VTV':'大型 Val','VBK':'小型 Gr','VUG':'大型 Gr'},inplace=True)2.ネギチャート作成処理
for ticker in data_stock.columns:
df_tmp=data_stock.loc[:,ticker]
fig, ax1 = plt.subplots(figsize=(8,6))
fig.patch.set_facecolor('black')
ax1.patch.set_facecolor('black')
# グラフ作成と光沢感を出す繰り返し処理
for n in range(1,10):
ax1.plot(df_tmp,linewidth=(2*n),alpha=0.4/(1*n),color='#00ff41')
ax1.plot(df_tmp,color='white',alpha=0.6,linewidth=1)
ax1.plot(df_tmp.iloc[:5],color='white',alpha=1.0,linewidth=10)
ax1.plot(df_tmp.iloc[-10:],color='white',alpha=0.8,linewidth=4)
ax1.plot(df_tmp.iloc[-8:],color='white',alpha=0.8,linewidth=6)
ax1.plot(df_tmp.iloc[-6:],color='white',alpha=0.9,linewidth=8)
ax1.plot(df_tmp.iloc[-4:],color='white',alpha=0.9,linewidth=10)
ax1.plot(df_tmp.iloc[-2:],color='white',alpha=1.0,linewidth=12)
ax1.scatter(df_tmp.idxmax(),df_tmp.max(),marker='o',s=500, color='white',edgecolor ='white',linewidth=20)
ax1.scatter(df_tmp.idxmin(),df_tmp.min(),marker='o',s=500, color='white',edgecolor ='white',linewidth=20)
ax1.scatter(df_tmp.index[0],df_tmp.iloc[0],marker='o',s=500, color='white',edgecolor ='white',linewidth=20)
ax1.scatter(df_tmp.index[-1],df_tmp.iloc[-1],marker='o',s=500, color='white',edgecolor ='white',linewidth=20)
# グラフ関連処理
ax1.tick_params(axis='x', colors='black',labelsize=12)
ax1.tick_params(axis='y', colors='black',labelsize=12)
plt.savefig(str(f'{round(df_tmp.iloc[-1]*100,):03}')+'_'+ticker + '.png',facecolor='black')
plt.close()
# ここまで3.K-means (k-means++)法によるクラスタリング
from glob import glob
import shutil
import cv2
import os
from sklearn.cluster import KMeans
import numpy as np
cls_num=20
# 画像読み込み、変形
img_paths = sorted(glob('./*.png') ,reverse=True)
X = np.array([cv2.resize(cv2.imread(img_path), (32, 32), cv2.INTER_CUBIC) for img_path in img_paths])
X = X.reshape(X.shape[0], -1)
# モデル作成
model = KMeans(n_clusters=cls_num,init = 'k-means++').fit(X)
# 過去の出力結果削除
for i in range(model.n_clusters):
cls_dir = './cls'+f'{i:02}'
if os.path.exists(cls_dir):
shutil.rmtree(cls_dir)
os.makedirs(cls_dir)
df_cls = pd.DataFrame()
# 結果をクラスタごとにディレクトリに保存
for label, img_path in zip(model.labels_, img_paths):
shutil.copyfile(img_path, './cls{}/{}'.format(f'{label:02}', img_path.split('/')[-1]))
df_cls=df_cls.append({'A':label,'B': img_path.split('_')[0], 'C':img_path.split('_')[1]},ignore_index=True)
df_cls.to_csv('out.csv')4.結果出力処理
import cv2
import glob
import numpy as np
from PIL import Image
from natsort import natsorted
from matplotlib import pyplot as plt
import math
%matplotlib inline
for cls in range(0,cls_num):
files = glob.glob('./cls' + f'{cls:02}' +'/*.png')
imglist = []
for file in files:
img = Image.open(file)
img = np.asarray(img)
imglist.append(img)
h_num = 8
v_num = math.ceil(len(files)/h_num)
plt.figure(figsize=(15,v_num*2),facecolor='white')
plt.subplots_adjust(wspace=0.1,hspace=0.1)
for i, item in enumerate(imglist):
plt.subplot(v_num, h_num, i+1)
img = Image.open(sorted(files)[i])
plt.imshow(img)
plt.title(sorted(files)[i].split('/')[2].replace('.png', ''),fontsize=15)
plt.axis('off')
print('Cluster ' + f'{cls:02}'+'\n')
plt.show()
print('\n')5.結果

結果を見てみると、レバナス、Netflix、半導体指数(SOXX)、小型グロースETF、Microsoft、コストコ、ラッセル2000などが並んでいる。まあ、レバナスに限らず、みんな同じように下落し、少し反発している状態である。
そんな中で、好調なのは下記のグループである。

最近のインフレと原油高を反映して、エネルギー関係のグループの株価を強い。
今回、クラスタリングの数は「20」とした。
下図は、クラスタ数と、クラスタ内の誤差を示したものである。誤差が急激に下がるポイントがあれば、そのグループ数が適切なのだが、とくに明確なポイントがあるようにも見えないので、多すぎない程度で大きい値に設定した。(グループにふさわしくないものが混ざっていると思われる時は、クラスタリング数を上げてください。精度は向上すると思います。)
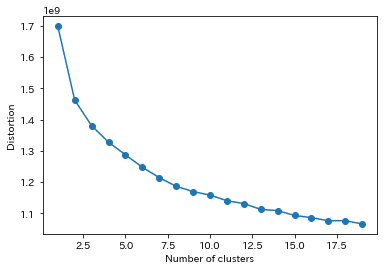
一応、最適クラスタ数をコードを調べるコードを記載しておきます。
6.K-means法の最適クラスタリング数を調べるコード
num=20
distortions = []
for i in range(1,num):
models = KMeans(n_clusters=i, init='k-means++', n_init=num, max_iter=50, random_state=0)
models.fit(X)
distortions.append(models.inertia_)
plt.plot(range(1,num),distortions,marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()今後の展開として、
今回、使用したクラスタリング機能を使って、大量のチャート群から、ベストパフォーマンスのチャートを作成するという試みを実施中です。
もしかしたら、良いチャートパターンが抽出できるかもしれません。
試行錯誤中ですが、ある程度、まとまったら記事にしたいと思います。
興味がある人はフォロー・いいねをよろしく!
今回の記事が、なにかの参考になれば幸いです。
では!
おつかれさん
「缶コーヒー、ご馳走してあげよう」という太っ腹な人は投げ銭を!
課金しなくても、参考になったら「ハートボタン、フォロー、リツイート」をお願いします。読まれる可能性があがるので、次の記事を書くやる気が出ます。
ここから先は
¥ 100
この記事が気に入ったらチップで応援してみませんか?
