第2266回 鳥の翼面荷重

①-1.https://jp.quora.com/より引用のひとの翼面荷重のイラスト

①-2.https://www.google.co.jp/amp/s/mainichi.jp/articles/20220629/k00/00m/040/126000c.ampより引用の人と翼竜ケツァルコアトルスとの比較

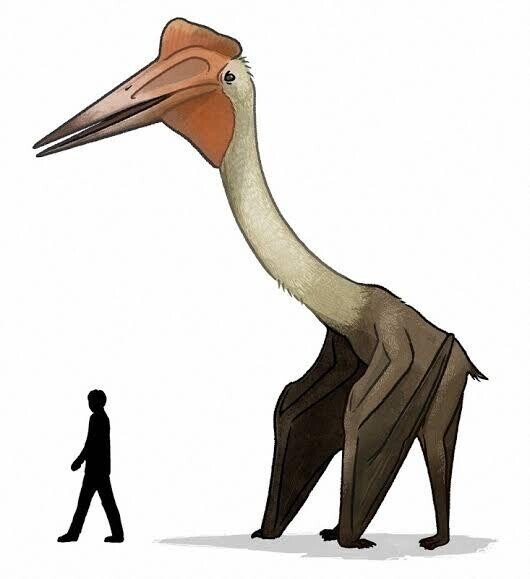
   昔からのひとの鳥への憧れに「どうすれば、あんな鳥のように空を飛ぶことができるんだろう」と鳥のように空を飛んでみたい気持ちはわたしにもあります。実際には人は動力などを用いなければ飛ぶことは不可能なんですが、机上の空論と致しまして、どうすれば自力で飛べるのか計算式を描いた人がいるみたいです。①-1.のイラストのように、もしも人間が鳥のように飛ぶためには翼の大きさはどのぐらい必要となるのか。もちろんそれを支え動かせるだけの筋肉が必要なので実際には無理です。①-2.のイラストは人と翼竜ケツァルコアトルスとの比較です。絶滅した翼竜のケツァルコアトルスは体重約70㌕と言われます。ほぼ人間と同じです。この翼竜は翼幅10㍍前後と推測されていますので、零戦並みの寸法です。零戦は翼面荷重が120kgf/m^2前後ですから、零戦と同じ速さで飛べれば翼面積は1m^2も要らないのですが、人はそこまで速く走れません。難しい原理のよう。

②http://silverrapide.blog94.fc2.com/blog-entry-270.htmlより引用のグンカンドリの仲間での翼面荷重の比較表

   鳥の体長が二倍になると体重は八倍になりますが
しかし重さを支える翼面積は四倍にしかなりませんが、大きい鳥ほど翼面積が不足致します。翼面荷重(よくめんかじゅう)とは、体重を翼面積で割った値で、一平方メートルの翼面積が何㌕の重さを支えるかを示しています。重い鳥ほど速く飛ばなければなりません。水平飛行や急降下時に翼を畳むと速くなります。日本で一番小さいとされまキクイタダキは1㌕、一番大きなハクチョウは体重が12㌕ありますので、約20㌕となります。大きい鳥ほど翼面荷重が大きくなります。翼面荷重の大きな鳥は飛行速度を大きくして、翼に生ずる上向きの力を増やさないと、重さを支えられなくなります。水平飛行に必要な速度は、翼面荷重の平方根に比例するから、大きさが二倍の鳥は√2倍にスピードアップしなければなりません。大きい鳥ほど筋肉も多く、大きい力を出せますが『水平飛行に必要なパワー』(速度×推力)の増加がどんどんこれを上回り、大きさの限界に達します。(理論上では17㌕、羽ばたいて飛べるのは12㌕)で、飛べる鳥の最大は十数㌕ですが、飛べない鳥は160㌖にも及びます。大きい鳥は体重1㌘当り片側0.6平方㌢の翼が必要。30㌕なら片側18,000平方㌢(巾1㍍×長さ2㍍)必要。難しい理論しか説明出来ない様子です。

③Xより引用の鳥の翼のアスペクト比

   鳥の翼には「アスペクト比」というものが存在します。「アスペクト比」とは、翼開長の二乗を翼面積で割ったもので、数字が大きいほど細長い翼で、効率よく飛行できますが、機動性が低く、離陸が大変で、森では枝にぶつかりやすい。アホウドリはその大きな身体を走るのも長い翼が邪魔をして、長い距離を助走して風を呼び込まなければ飛び上れません。また、着陸も長い翼が災いし、着地に失敗して草原の中に頭から突っ込み、一回転して仰向けにひっくり返った状態で両足をバタつかせ、何事もなかったように起き上がります。数値の違いを若鳥ねイヌワシて比較したデーターで見てみましたら、こんなに違いがあります。         ⑴  イヌワシ(若)→❶  翼幅(㍍)  1.63   ❷  翼面積(平方㍍)  0.431   ❸  アスペクト比  6.2   ❹  体重(㌕)  1.8   ❺  重量(N)  18   ❻  翼面荷重(N/㎡)  41     ❼  推定最小抵抗係数  0.013
⑵  アホウドリ→❶  3.00   ❷  0.67   ❸  18   ❹  10   ❺  98   ❻  147   ❼  0.007  

④-1.https://amanaimages.com/info/infoRM.aspx?SearchKey=01543047402より引用の飛行するカラフトフクロウ(体長約61〜84㌢)

④-2.https://www.naturingnews.jp/?p=24662より引用の飛翔するイヌワシ(体長約81〜89㌢)

   ここで、翼面荷重を使いフクロウの仲間の巡行速度を算出してみました。m/sはメートル毎秒です。  ⑴  フクロウ→❶  体重(g)  650   ❷  翼面積(c㎡)  2,000   ❸  翼面荷重(g/ c㎡)  0.33   ❹  アスペクト比  5.0   ❺  巡航速度(m/s)  9.2                                    ⑵  メンフクロウ→❶  300   ❷  1,200   ❸  0.24
❹  8.3   ❺  8.0                                                            ⑶   カラフトフクロウ→❶  1,300   ❷  3,700 
❸  0.35   ❹  6.1   ❺  9.5                                         ⑷  ワシミミズク→❶  2,200   ❷  3,100   ❸  0.71
❹  8.3   ❺  13.5                                                       もうひとつの猛禽類として、タカの仲間はどうか   ⑴  チュウヒ→❶  700   ❷  2,200   ❸  0.32
❹  8.0   ❺  ー                                                             ⑵  オオタカ→❶  750   ❷  2,600   ❸  0.27
❹  6.0   ❺  ー                                                              ⑶  ハヤブサ→❶  850   ❷  1,300   ❸  0.62
❹  8.6   ❺  13.0
⑷  ノスリ→❶  1,000   ❷  2,700   ❸  0.38
❹  7.0   ❺  ー                                                                 ⑸  イヌワシ→❶  3,700   ❷  5,400   ❸  0.70
❹  8.0   ❺  ー                                                            

⑤-1.https://www.birdfan.net/2019/02/15/68109/より引用の飛翔するカモメ(体長約49㌢)

⑤-2.https://jp.123rf.com/free-images?r=dより引用の飛翔するワタリアホウドリ(体長約110〜140㌢)

⑴  アジサシ→❶  115   ❷  500   ❸  0.23               ❹    ー     ❺  7.8
⑵  ユリカモメ→❶  230   ❷  750   ❸  0.31           ❹    ー     ❺  9.0                                                          ⑶  カモメ→❶  370   ❷  1,150   ❸  0.32                ❹    ー     ❺   9.2                                                     ⑷  ミツユビカモメ→❶  490   ❷  970   ❸  0.51    ❹    ー     ❺     10.1                                                      ⑸  フルマカモメ→❶  820   ❷  1,240   ❸  0.66     ❹    ー     ❺   13.2                                                     ⑹  セグロカモメ→❶  1,100   ❷  2,100   ❸  0.52  ❹    ー     ❺   11.7                                                        ⑺  オオトウゾクカモメ→❶  1,350   ❷  2,140          ❸  0.63   ❹    ー     ❺  12.9
⑻  オオカモメ→❶  1,900   ❷  2,700   ❸  0.71     ❹    ー    ❺  13.6                                                       ⑼  ワタリアホウドリ→❶  8,700   ❷  6,200            ❸  1.40   ❹    ー    ❺  19.2