このウツロパズルには必勝法がある（謎解きに関するネタバレあり）

2024年1月12日 23:05

※本記事は「ウツロマユ」の謎解きに関するネタバレが含まれます（ストーリーに関するネタバレは含まれておりません）

　近年、欧州サッカーに匹敵する市場規模に迫りつつあると噂されるeスポーツ「ウツロマユ RTA」ですが、その中で大きなタイムロスの原因となっているのが、仏間にあるパズル（通称：ウツロパズル）です。

　要は、4 つの円盤を回転させて、中心を「緑→青→赤→黒」（緑が上）に揃えるゲームですが、頭がこんがらがってミスをしがちです。

　しかし、RTA においては 1 秒でもタイムを縮めたい。どうにかならないものか……。

秋山「このゲームには必勝法がある」
「!?」
秋山「マス目は 12 通り、有効なコマは区別のある 4 種類」
秋山「つまり、ありえる状態数は $${_{12} P _4 = 11,880}$$ 通り」
秋山「回転の処理を考えても高々 $${10^6}$$ オーダー」
秋山「通るんだよ、全探索が。1秒足らずで」

　という訳で、プログラムで全探索します。以下は C++ による実装です。

// include やマクロの類は省略

string clockwise(string s, int start)
{
    swap(s[start], s[start + 4]);
    swap(s[start + 4], s[start + 5]);
    swap(s[start + 5], s[start + 1]);
    return s;
}

string counter_clockwise(string s, int start)
{
    swap(s[start], s[start + 1]);
    swap(s[start + 1], s[start + 5]);
    swap(s[start + 5], s[start + 4]);
    return s;
}

int main()
{
    map<string, int> mp;
    queue<string> q;
    vector<int> starts = {1, 4, 6, 9};
    string s = "x..x.GB..KR.x..x";
    mp[s] = 0;
    q.push(s);
    while (q.size())
    {
        string now = q.front();
        q.pop();
        for (int start : starts)
        {
            string cw = clockwise(now, start);
            if (!mp.count(cw))
            {
                mp[cw] = mp[now] + 1;
                q.push(cw);
            }
            string ccw = counter_clockwise(now, start);
            if (!mp.count(ccw))
            {
                mp[ccw] = mp[now] + 1;
                q.push(ccw);
            }
        }
    }
}

　アルゴリズム的に表現すると、「x..x.GB..KR.x..x」という文字列の並び替え（ただし x は固定）をノードとした幅優先探索です。

　もちろん、このままではなんのこっちゃという感じだと思うので、わかりやすく図示した結果を以下に示します。

結果

　詰将棋にならって、$${x}$$ 手詰という形で表記します。

1 手詰（8 種類）

　完成形から 1 つずらしたものは全て 1 手詰になります。以下のような「へ」の字になっている形です。「へ」の字になっている時はリーチだと覚えましょう。ただし、色の並びが違う場合は注意です。

2 手詰（44 種類）

　ちょっと量が多いですが、以上の形が 2 手詰です。選択肢が多いのに、ここを外すと大きなロスが出ます。麻雀でいえば一向聴、いわば一番実力が出る部分ですね。「ウツロマユ RTA のプロ走者は 2 手詰を外さない」とは良く言われるところです。

その他解析

（※1/14 追記　最初に載せた解析にミスがあり、この項目の結論を修正しました。その時は最悪手は 10 手詰であると述べましたが、正しくは 9 手詰になります）

　$${x}$$ 手詰と対応する盤面の種類 $${n}$$ は以下の表の通りになります。

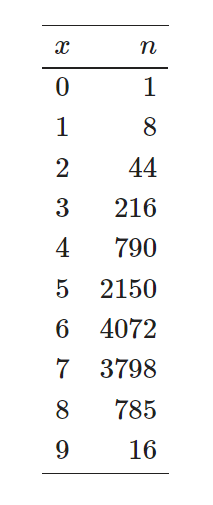
　一番、状態数が多いのは 6 手詰の時で、4072 通りになります。また、一番完成形から遠いのは 9 手詰です。言い方を変えれば、ウツロパズルはどのような極悪な配置でも、必ず 9 手以内に完成させられると言えます。

　ちなみに、以下がそのような最悪配置（16 種類）です。走っている時にこれを引き当てたら最悪です。

おまけ：将来の夢（？）

　アルゴリズム的には完全に解析完了したので、RTA 走者向けに、このパズルを訓練する Web アプリ（最短経路以外の選択肢を選んだら強制ゲームオーバー）でも作ろうかと思いましたが、UI の実装がめんどくさそう＆ホスティング（もしかして DB も？）を確保するのにも料金がかかるかも、ということで、優先順位はそこまで高くないです。

　極めて限られた需要だと思いますが、実現して欲しいという方がいたら……気長に待ってください。すいません。

おまけ：現実的な攻略法

　ちなみに、私が実際に走る時は、以下のような配置にすることを実質なゴールにしています。

　左上から時計回りに「緑、黒、青、赤」ですね。それぞれのコマ同士を離すようにしていけば、それほど難しくありません。

　後は、黒→青→赤を中心に寄せて、緑黒を時計回りに回転させれば完成するという、簡単な 4 手詰になります。

　まあ、このレベルの攻略法だと、もっとマシな戦略をすでに実践しとるわ！　という走者も多いと思いますが、何かの参考になれば。