
【フラクタル解説】FNFE Project #25「25時、カオスの縁で」
あああああああああ最近受けが悪いあああああああああああどうもこんにちは。FNFE Projectへようこそ!
FNFE Project「実戦」では、今までのフラクタルの基礎的・標準的な知識をベースに、より踏み込んだことについて探求・探究していきます。
さらには関わりの深いカオス理論・カオス力学系とも絡めながら最終的には複雑系への理解を深めていきます。
今回は「セル・オートマトンとフラクタルの関わり」を解説します。私の得意分野です。10歳くらいから触れてました。なのではしゃぎます。
①-DᴇғIᴹᴱNˢɪτION
多分皆さんこう思っていますよね。
「セル・オートマトンってなんやねん?????」って。ということで解説おにいさんが解説してくれるそうです。
(解説おにいさん)みなさんこんにちは。早速解説していきましょう。
セル・オートマトンとは、格子状のグリッドのマス目と、それらの変化のルールからなる単純な計算モデルです。
話の流れ上便利なので、まずは一次元セル・オートマトンについて解説します。分かりやすくするために少し変則的な説明の仕方をしますが許してください。
無限に広がる格子を考えます。この格子においてそれぞれのマス目をセルと呼びます。

それぞれのセルには2パターンの状態があり、各セルの色で表されます。ここでは黒のセルを「死んでいるセル」と、白のセルを「生きているセル」と呼びます。
左側が生きているセル、右側が死んでいるセルです。何も見えない?是非心の目で感じ取ってください。
次に格子上でのルールを定義します。一次元セル・オートマトンでは、中心のセル(黄色)に対する上部のセル(青色)に注目します。
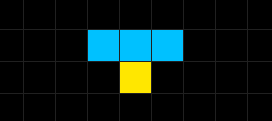
このとき、ひとつのセルに対する上部のセルには8種類の状態が考えられますよね。

ということでこれらを基にして変化のルールを決めていこうと思います。
セル・オートマトンには世代という概念があり、元の世代に対する次の世代は変化のルールが適用された状態となります。
例えば以下のような変化のルールを考えます。
・死んでいるセルの右か左どちらか一方のみが生きている場合、そのセルは生きているセルに変化する
・そうでない場合、死んでいるセルはそのまま
・生きているセルの左右のセルが共に生きている場合、そのセルは次の世代でも生きたまま
・そうでない場合、そのセルは死ぬ
このようなルールで世代ごとのセルの変化を見ていくと、以下のようになります。上から順に0世代(初期状態)、1世代、2世代…の順で並べていっています。
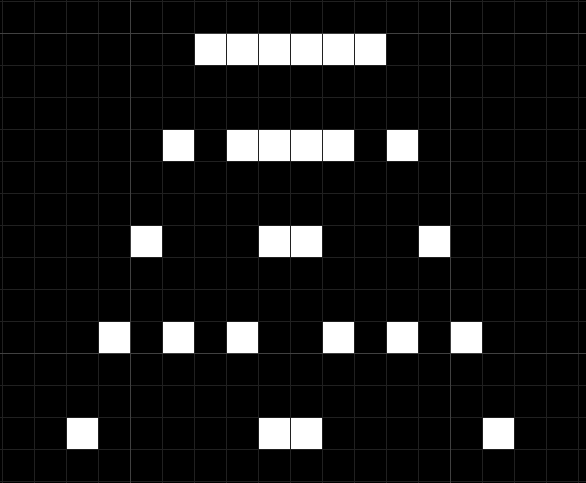
要は世代というのはステップみたいな概念で、世代を経るとルールに従って各セルの状態が変化する、というのが分かれば大丈夫です。
世代の間隔はつかめたでしょうか。ここからは一次元セル・オートマトンでのルールについて詳しく見ていきます。
まず一次元セル・オートマトンでは一度生きている状態になったセルは二度と死ぬことはありません。
次にセルが生まれる条件を定義します。黄色のセルに対し青色のセルが特定の状態の時生まれ、そうでないときは死んだまま、と言うものを考えます。この言わば誕生条件の組み合わせは256種類考えられ、0-255までの数字で表されます。具体的には、セルが図の配置の時に誕生するなら、それらの上の数字の合計がルールを表す数字となります。
例えば先ほどのルールは「128,16,2」の配置で誕生すると言い換えられるので、ルール番号はそれらの合計である146となります。
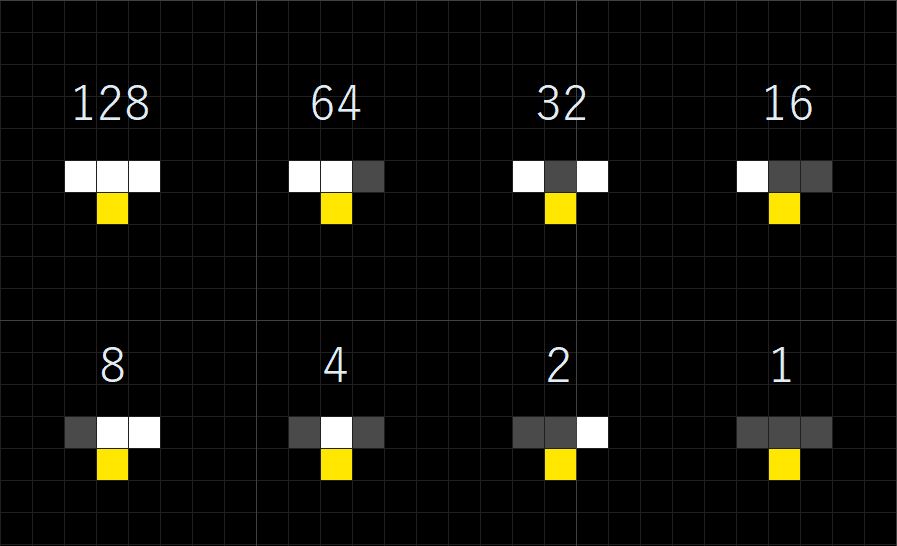
他にも110=64+32+8+4+2なので、ルール110は以下のような配置の時に生まれる、とわかります。
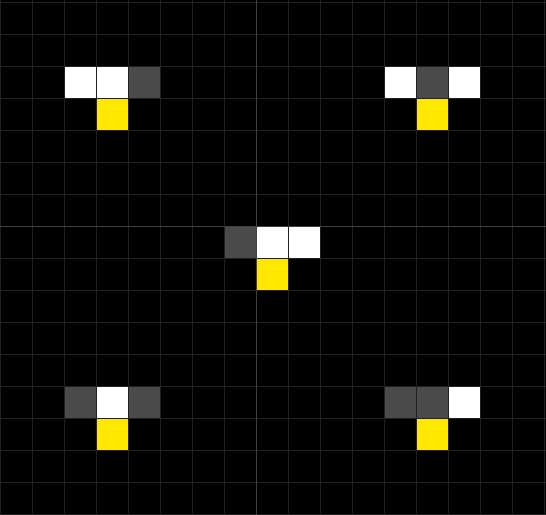
ちなみにこれは覚えなくていいんですが、セル・オートマトンの挙動は4パターンに分類出来て、
①クラス1…死セルだけ、生セルだけという状態に収束するもの
②クラス2…周期的で予測できる状態に収束するもの
③クラス3…予測不可能でランダムな変化をするもの
④クラス4…上記のいずれにも当てはまらないもの
が存在します。

このとき、④では複数の要素が絡まり溶け合い、また創発しあう特性が表れます。

クラス4のセル・オートマトンは非常に狭い安定と不安定の境目となる領域に位置し、ここでは予測不可能なのにランダムではない、非常に複雑な動作を見せます。このような領域をカオスの縁と言います。
一次元セル・オートマトンのルールとしては以上となります。ありがとうございました。
ということで一次元セル・オートマトンとフラクタルの関わりを見ていきましょう。
一次元セル・オートマトンの中には世代を進めていくとフラクタル図形が生成されるものがいくつかあります。例えばルール18の場合はどのような図形が生成されるでしょうか?
最初の11世代目は以下のようになっています。この時点でなんか察した人はいい視点を持っている方です。分からなくても大丈夫ですからね!??!?!

255世代目まで進めるといい感じに見えてくるはずです。

そうです!!!シェルピンスキーのギャスケットです!!!!!!

これでシェルピンスキーのギャスケットを生成する方法に4つ目が追加されました。
①カオスゲーム(行列)
②カオスゲーム(中点)
③L-system
④これ
で、初期状態が生きているセルひとつだけの状態からシェルピンスキーのギャスケット(以降面倒臭いのでシェギャと言います)を生成する1次元セル・オートマトンは他にもあります。全て列挙すると以下のようになります。
18, 22, 26, 60, 82, 90, 102, 126, 146, 154, 182, 210, 218
129, 161, 165, 167, 181, 195
ただ、一口にシェギャを生成するといってもその生成法はルールごとに微妙に違ってきます。
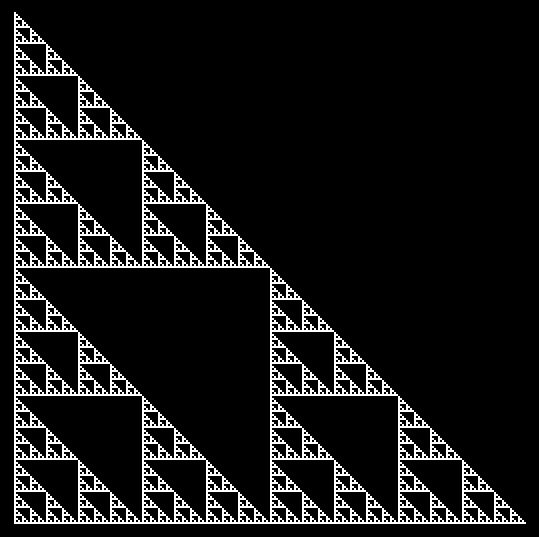


また、「1点だけを初期状態としてもシェギャは登場しないが、それ以外の初期状態では出現し得る」というルールも存在します。

シェギャ以外のフラクタルを生成するルールには2種類あります。
ひとつがルール150で、これは以下のようなフラクタルを生成します。

反復関数系で以下のように表現されるものを2つくっつけた形になります。

もうひとつがルール106⇔120, 169⇔225(それぞれ左右対称・白黒反転の関係)で、以下のようになります。是非アナモルフォーシスで感じ取ってください。
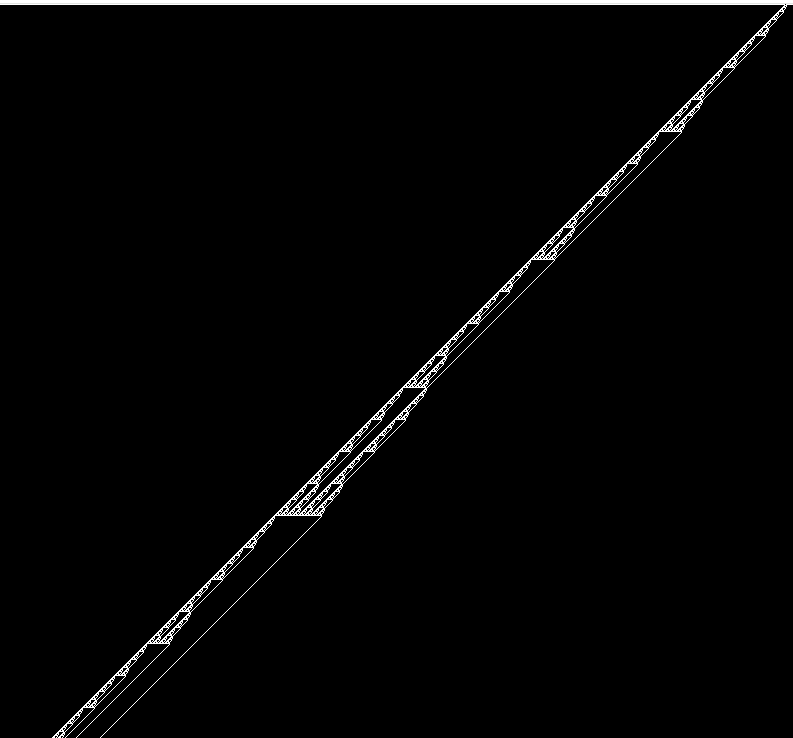
BL[i/o][n/c]K[er/_]
続いては範囲を二次元に広げてライフゲームの紹介です。おにいさあああああああ
(解説おにいさん)はいはい。ということでライフゲームの解説です。
まず先程と同様、格子と生きているセル、死んでいるセルを用意します。
次に、「周り」を上下左右と斜めに直接接触している8つのセルと定義し、以下のようなルールを考えます。

・中央のセルが死んでいるセルの場合、
①周りに生きているセルが丁度3つある場合、そのセルは生きているセルになる
②そうでない場合はそのまま
・中央のセルが生きているセルの場合、
③周りに生きているセルが丁度2つか3つある場合、そのセルは生きているセルのまま
④そうでない場合は死ぬ
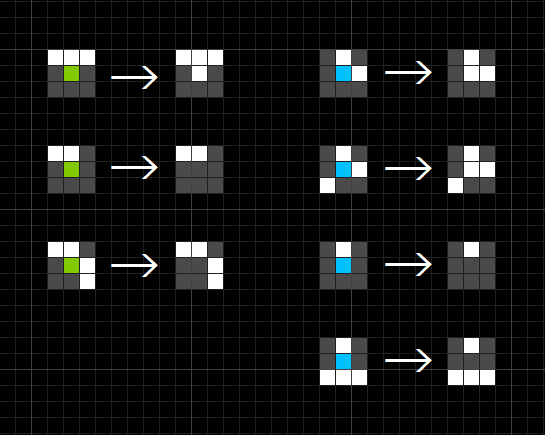
というようなルールから定義されるセル・オートマトンをライフゲームと言います。ではさよなら。
ライフゲームでフラクタルを生成する最も簡単な方法は十分長い厚さ1セル分の線分を縦か横に引くことです。ということで…

32768セルの長さの線を引きました。
そんなんは置いといて世代を進めていきましょう。900世代ほど進めると片鱗が見えてきます。

さらに進めるとこうなり

こうなった後

こうなります。

なんか周りに飛び散っている奴はグライダーというパターンで、4世代ごとに斜めに1マス移動するものです。

詳しく話すと連載記事がもう一本書けてしまうので簡単に留めますが、パターン、つまり平面上のセルの集合には主に4つに分類でき、
①固定物体…世代を進めても状態が変化しないもの
②振動子…一定世代経つと元の形に戻るもの
③宇宙船…一定世代すると元の形に戻るが、元の位置から移動しているもの
④無限成長…セル数が無限に増えていくもの
があり、グライダーは3番に当てはまります。これら以外にもいろいろありますが主に注目されるもの、及び覚えておくべきものはこれらとなります。
なぜこのような模様が生成されるのか、というメカニズムは案外単純です。
まず解説のためにトーラス平面という概念を導入します。仕組みは単純、平面を有限にし、端と端をつなげるだけです。
横幅が無限で縦が16マスのトーラス平面を考えます。ここで縦線を引くと、その動きはルール22に従います。


ここで平面を有限のものに戻し、今度は線の端に注目します。こんな感じになっていますが、

これがこうなって

こうなった後

こうなります。

このとき)の形をしたやつが生成されていますね。これは生きているセルの線に沿って生成されるので、これらの相互作用によりシェギャの大まかな形が生成されるわけですね。
ちなみにライフゲームなどいくつかのセル・オートマトンは初期値鋭敏性がエグく、1セルでも初期状態が違えば全く異なる変化をしていきます。
例えばこのパターンは
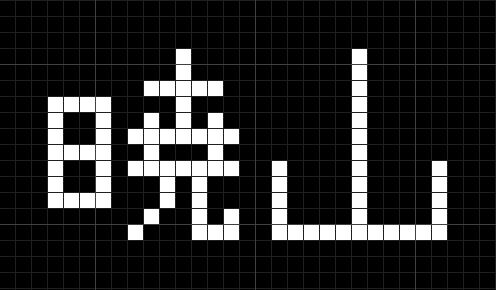
こうなりますが
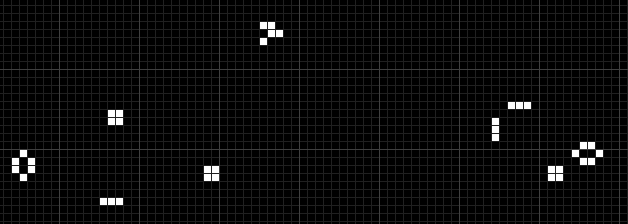
初期配置を1セルだけ変えたこれは
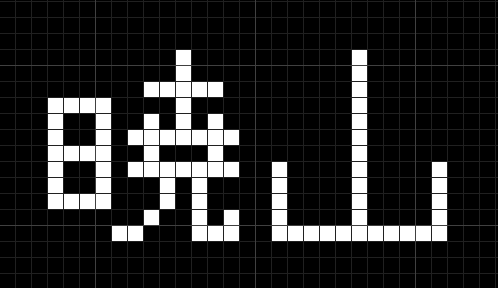
こうなります。

AN eXplosIvE rule TrYings
ここからはLife-like cellular automaton(めんどくさいので以降LLCA)についてやっていきます。
ライフゲームでは、
・誕生条件…死んでいるセルは周囲の生きているセルが3つのときにセルが生まれ、
・生存条件…生きているセルは周囲の生きているセルが2つか3つのときに生き残る
というルールでした。このとき、誕生条件の「3」や生存条件の「2, 3」という数字を変えてみるとどうなるのかな~ってのがLLCAです。
生セルが死セルにn個隣接しているとき生まれ、生セルに生セルがm個隣接しているとき生存する、とすると、そのようなルールはBn/Smと表されます。ライフゲームだとB3/S23ですね。というわけで見ていきましょう。
まず、B3/S28というルールを考えます。これは誕生条件はライフゲームと同じですが、生存条件が「周りに2個か8個の生きているセルが存在する」と変わっています。
このルールで超長い線を初期配置として変化を見ると…??

あ、なんか出てますね。ルール150で生成されるフラクタルが出てきました。

拡大すると以下のようになっています。是非PCの背景にどうぞ。

B36/S28とすると白黒反転版のシェギャみたいなのができますが、欠けている部分があります。


(解説はてなくん)ねえもう線は飽きたよ。違うのが見たい。
(私)俺も飽きた。てかこれ以上線を調べることない。ってことで!!
今から取り上げるのはReplicator(自己複製子)です。これは以下のような特性を満たすパターンです。
・一定世代後に元の形が複数並んだ状態に変化する
・無限に大きくなる
例えば、B36/S23というルールで以下のようなパターンを考えます。

このパターンは12世代経つと2つに分裂したような形になります。
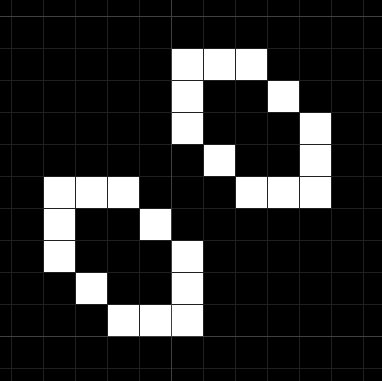
さらに世代を進めても、この形が増減を繰り返しながら無限に複製されていきます。
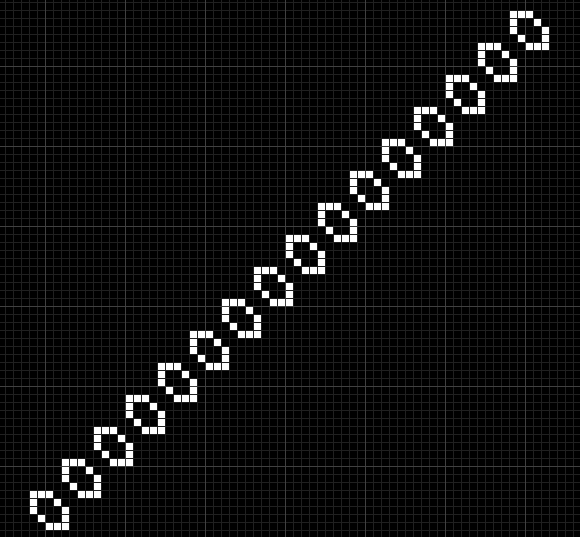

このReplicatorはルール90に従って無限増殖を続けていくんですね。
さて、このReplicatorを無限に生産するようなパターンがあったらどうなるでしょうか?
以下のパターンは本体が移動しながら96世代ごとにReplicatorを生成します。
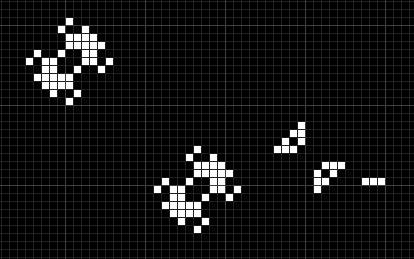
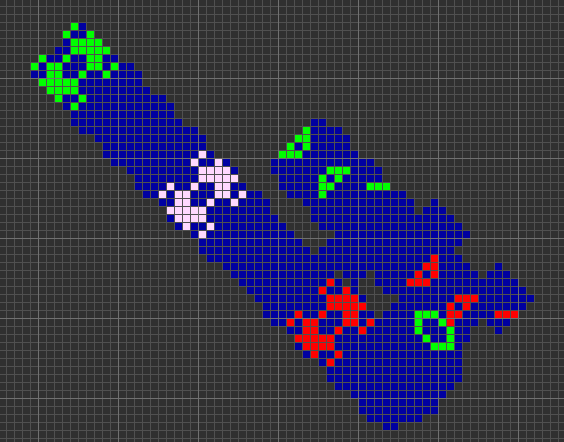
ピンクは赤と緑が重なるところ
では実際に動きを見てみましょう。

はいはいシェギャシェギャ。画質が逝ってしまいましたがそれでもシェギャと分かるくらいにはシェギャです。
ちなみに、B36/S23のReplicatorの生セル数は定期的に24に戻るので、世代数を横軸に、生セル数を縦軸にとってグラフを描くとまた新たなフラクタルができます。
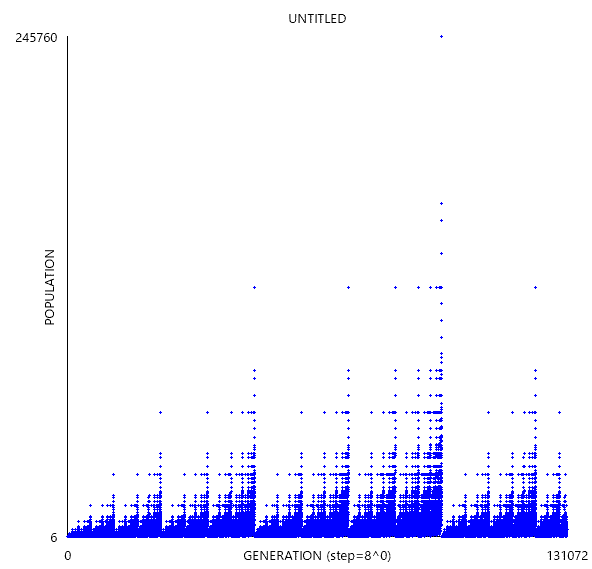
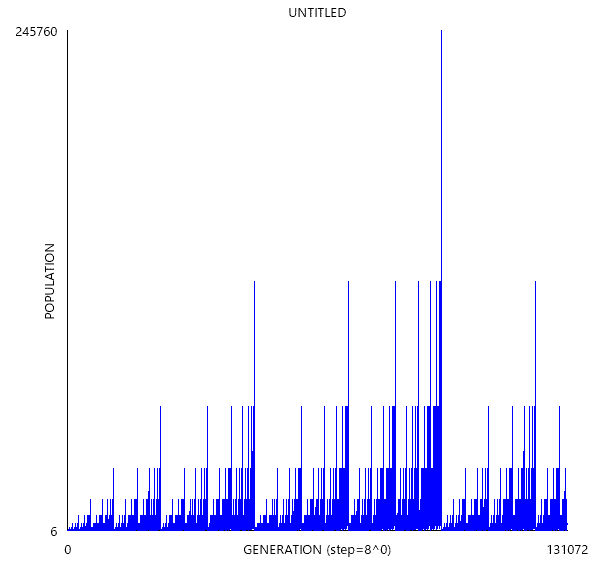
続いて、B1357/S1357というルールを考えます。このルールはどんな初期配置を取ろうが、全てのパターンがReplicatorになるという珍しい特性を持っています。(ちなみにB1357/S02468もそのような特性を持ちます)

初期配置を一つの生セルだけにして、先ほどと同様に生セル数と世代数のグラフを取ってみるとこうなります。
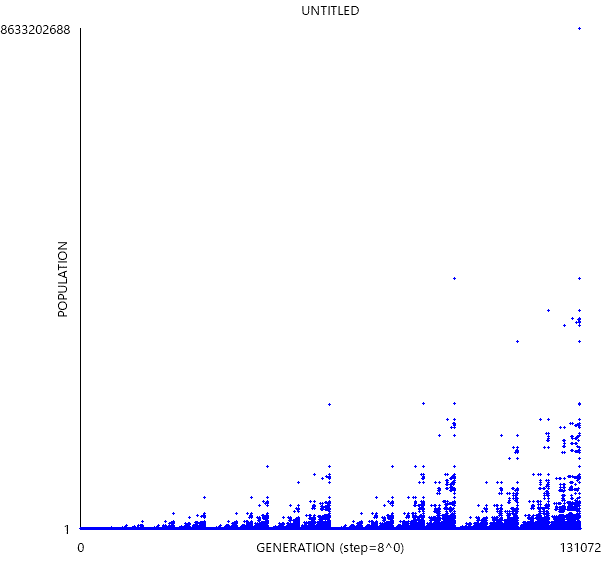
見るからにフラクタってますね。
他のルールでもグラフを取ってみましょう。以下はB13/S08、初期配置は単独生セルです。
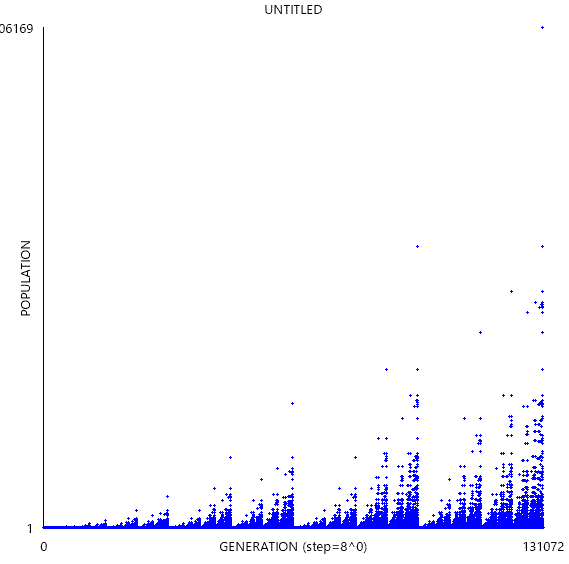
さっきと同じに見えますが、初期配置を以下のように変えるとこうなります。

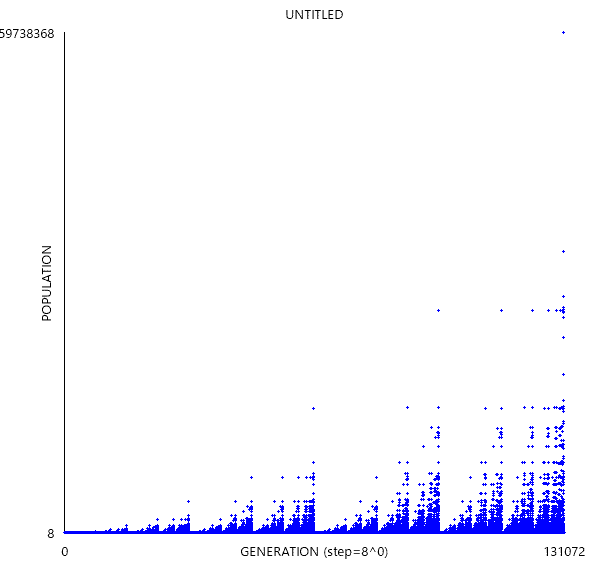
以下はB1/S、初期配置は単独生セルです。
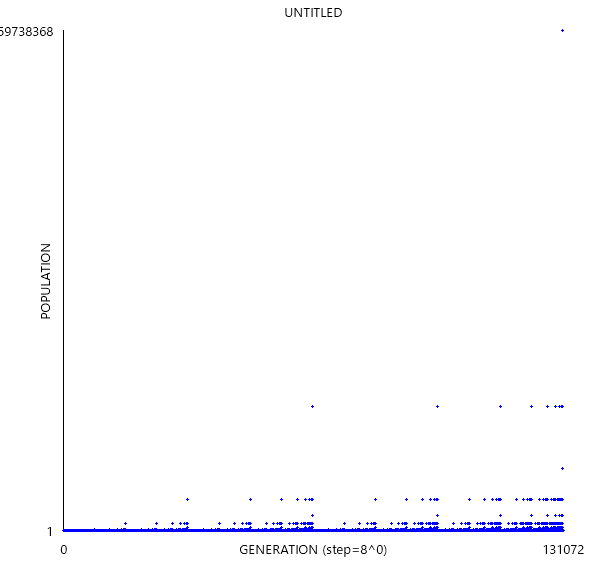
また、B36/S245では世代数をtとすると生セル数が√tに比例する、というようなReplicatorも存在します。

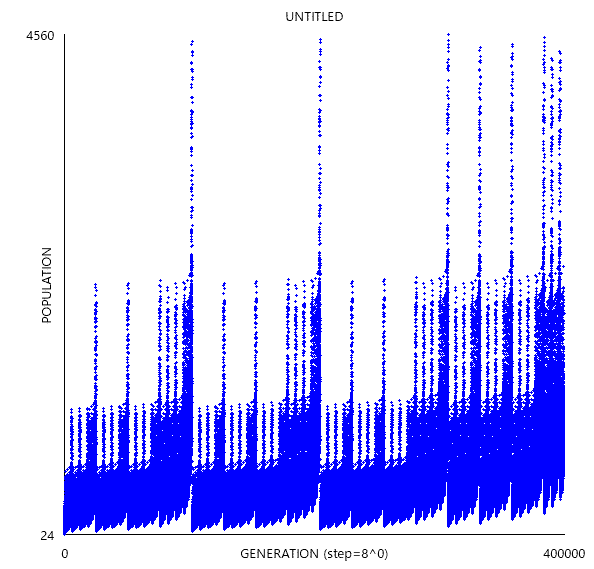
Replicatorをベースとする場合、個々の見た目はフラクタルっぽくないけど生セル数の増減のグラフはフラクタルになる、というケースが多いようです。
他にもB3/S012345678などでは拡散律速凝集に似た模様が見られます。
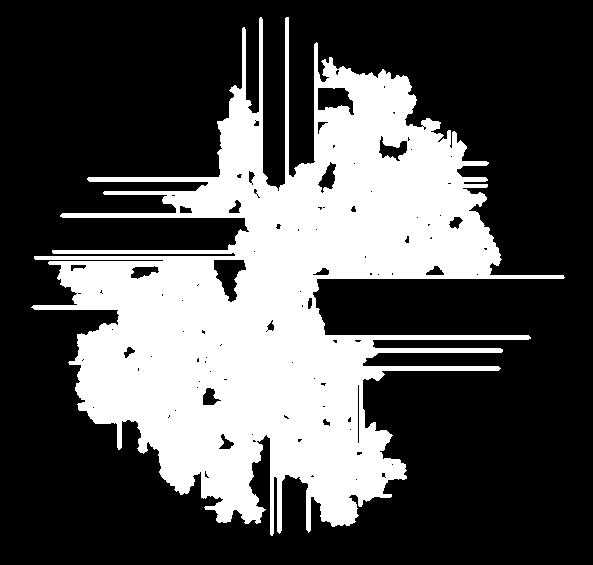

これはB1/S012345678です。「T-square」というフラクタルが生成されます。


色々なルールを見てきましたが、まだ自由度やバリエーションが足りない気がしますよね。ということでさらに拡張していきます。
isoTROPICᴬᴸ_Nightmare
というわけでここから更に深い世界、Isotropic Non-Totalistic Cellular Automaton(だるいので以降INT)について追っていきます。
INTでは「周囲に何個セルがあるのか」だけでなく「周囲のセルがどんな配置か」によって誕生・生存するか否かが分けられます。
INTのルールを表記する方法として現在主なものがHensel Notationです。
まず、この表を見てください。ってか覚えて下さい。

で、先ほどと同様Bn/Smで誕生・生存条件を表記していきますが、これが引くほど複雑です。
①k個のセルが接しているとき無条件に誕生・生存するなら、B・Sの配列にkを加える
②上の数字をN、左のアルファベットをMとする。セルの配置がNMで表される時に誕生・生存するなら、B・Sの配列にNMを加える
③共通のNを持つ複数のNMが配列に存在する場合、まとめてNM₁M₂M₃…で表記する
④k個のセルが接しているとき誕生・生存するが、例外的に周囲のセルの配置がkMの場合誕生・生存しないとき、k-Mで表す
⑤例外条件が一つのkに複数存在する場合、k-M₁M₂M₃…というようにまとめて表記する
⑥NMについては向き・上下左右を問わない(=等方性、Isotropic)
分かりやすくするためにいくつか例を取って解説します。
まず、通常のライフゲームに以下のようなルールを追加したい場合はどうすればよいでしょうか。
・図上部のような配置の時、中央のセルは誕生する
・図下部のような配置の時、中央のセルは死亡する
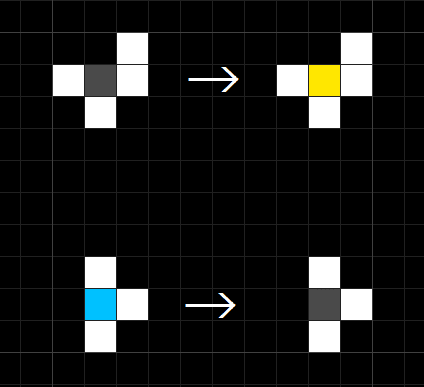
まず対応する誕生・生存条件を表から見つけてきます。上は4j、下は3eに当てはまりますね。
次にB、つまり誕生条件とS、つまり生存条件を書き換えます。4jを追加するだけなので、BはシンプルにB34jですね。また、Sは3から3eを取り除くのでS23-eとなり、合わせるとB34j/S23-eとなります。完成!!!!
第2話:さらにこれを追加しろ。
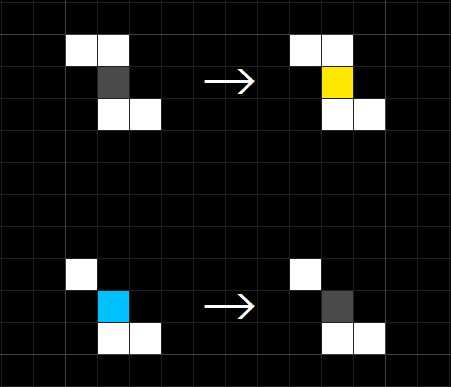
まあB4zの追加とS3qの削除だけで済むんですが、③⑤のルールから同じ数字の時はまとめて表記するので、B34jz/S23-eqとなります。文字はアルファベット順で並びます。
なかなかえぐい自認あんのかって話ですね。ちなみに私は全て覚えています。全部覚えたら私に自慢してきてください。
さて、LLCAは2¹⁸=262,144種類存在しますが、INTは2¹⁰²=5,070,602,400,912,917,605,986,812,821,504(約5071穣)種類と、実に2⁸⁴=19,342,813,113,834,066,795,298,816(約19𥝱倍)あるわけなのでLLCAより遥かに豊かな挙動を見せます。宇宙がいっぺん終わるくらいの時間がないと全部探査し切れないですね。というわけで見ます。
INTになるともう見ただけでフラクタルと分かるReplicatorも存在します。以下はB1c/S04c、初期配置は生セルひとつです。

他にも単独生セルを初期配置としてできるフラクタルを見ていきましょう。ルールは画像の下部に表示してあります。




というわけで一旦B1系から離れて、次はB2a系ルールを見ていきましょう。
まず、B2aei/S0というルールを見ていきます。このルールで以下の初期状態から始めると…

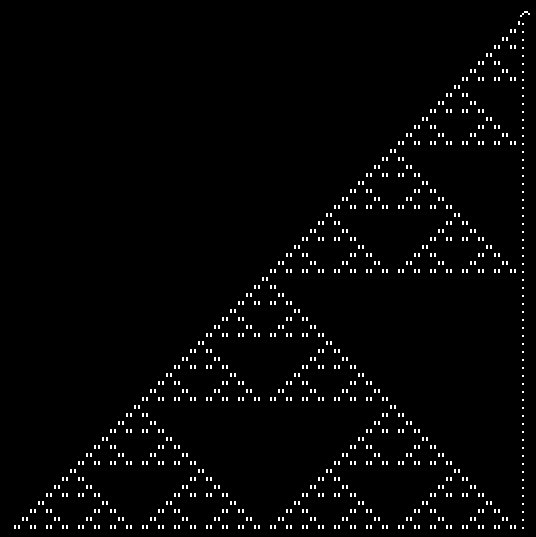
シェギャです。
このルールでは縦に2つ並んだ生セルが、B36/S23のものと似たような動きをするReplicatorとなります。左半分しか生成されていないのは、点がReplicatorに対するストッパーの役割をしているからです。
で、これを2個つなげると…
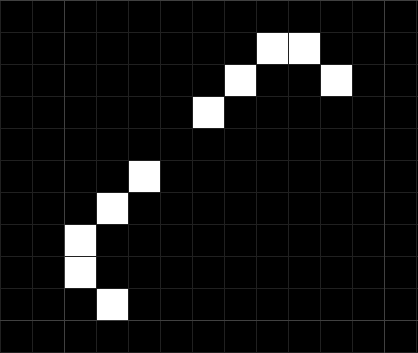


傾きや角度、引き伸ばされ具合(うまい表現がなかった)が異なるシェギャが複数重なったような図形が登場します。
世代を進めると模様が動く様子を動画にしました。動くフラクタルということで二例目ですね。
続いてはB2ae/S1eからの紹介です。以下のような配置で実行すると…
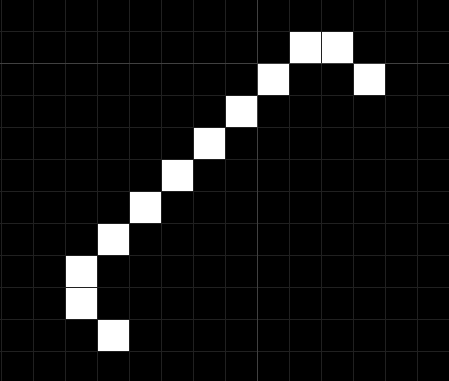
こうなります。

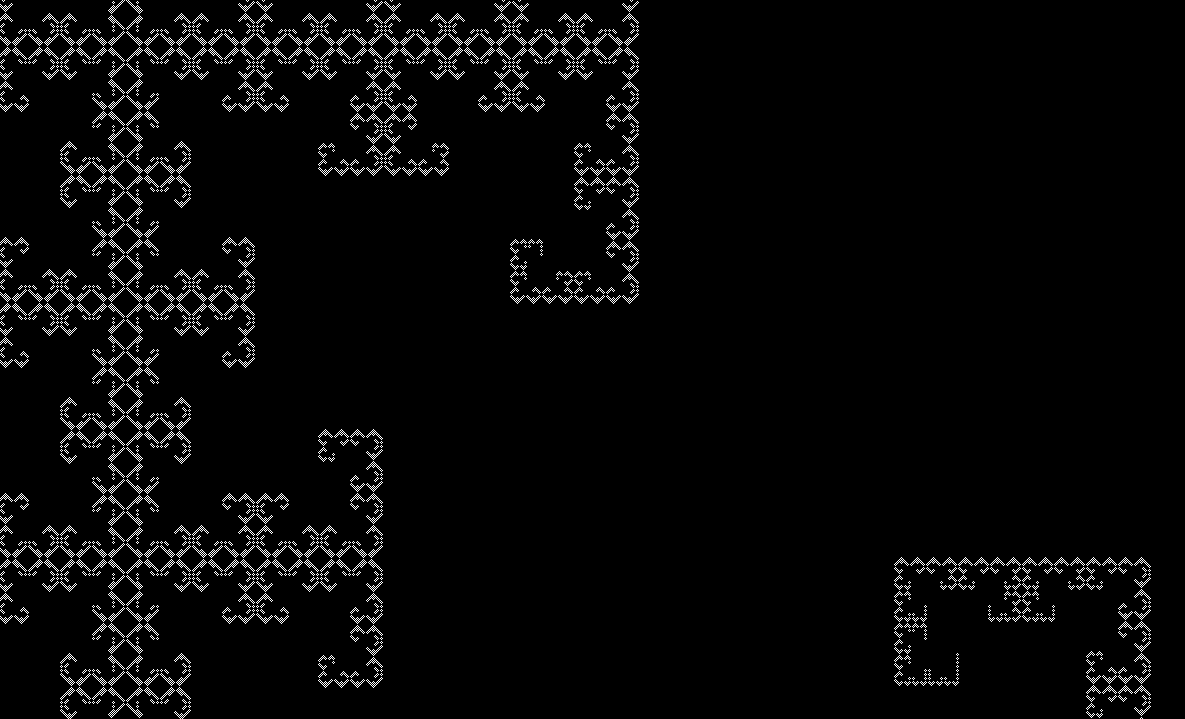
T-squareの右下だけ取っ払ったみたいなやつが登場しますね。
同じ初期配置をB2ae4c/S1eでやるとこうなります。
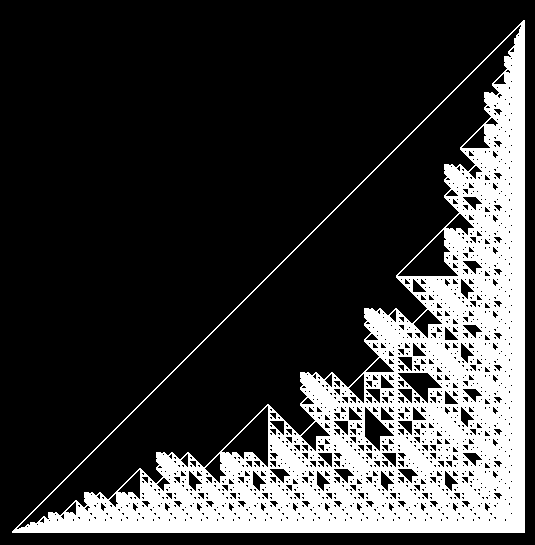
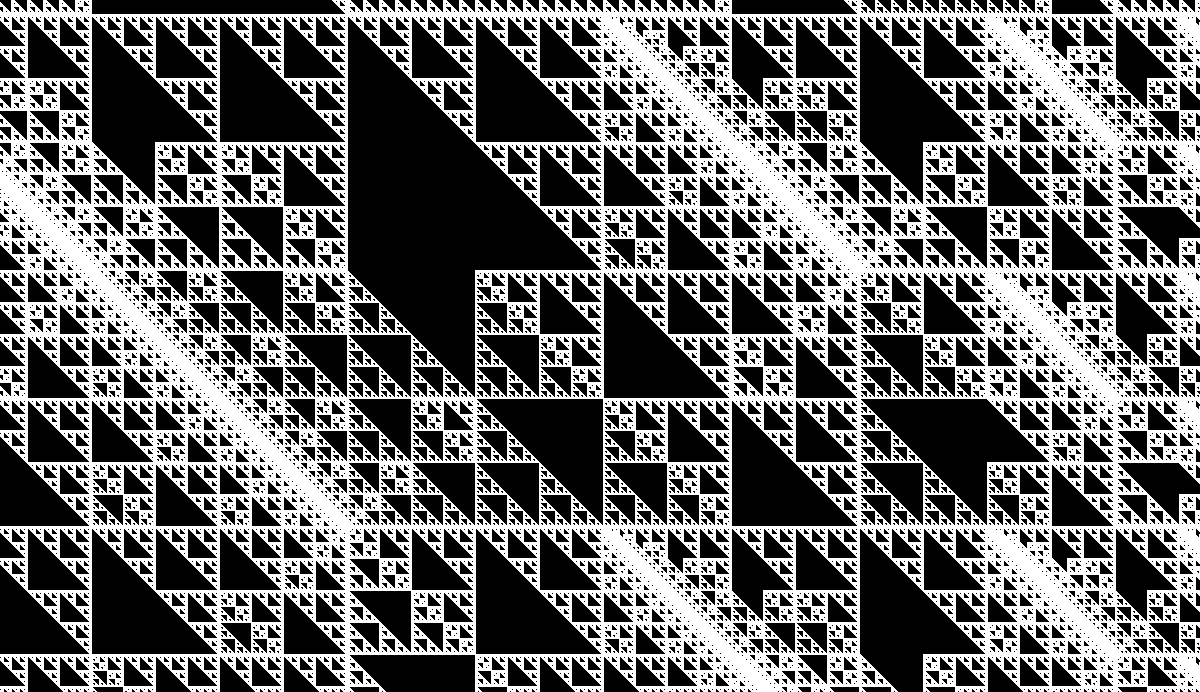
なんかすごいですね。
他にもB2ak3nr4iy/S3-nr4ent5erというルールではRuler Functionのような模様が生成されることがあります。

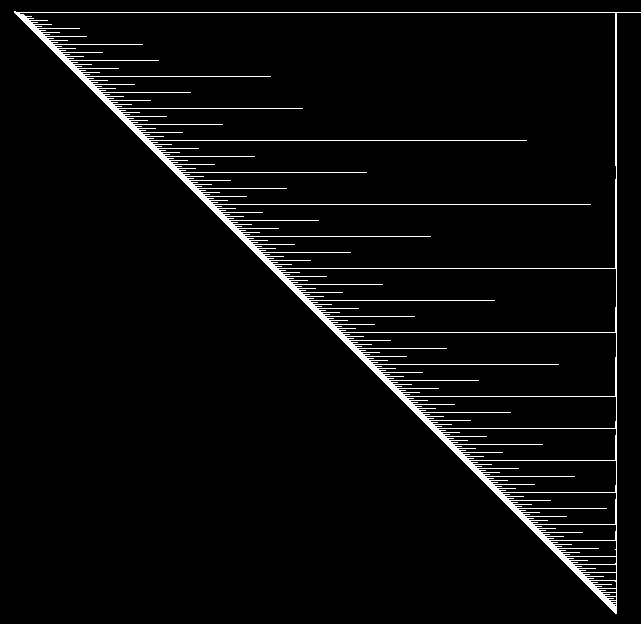
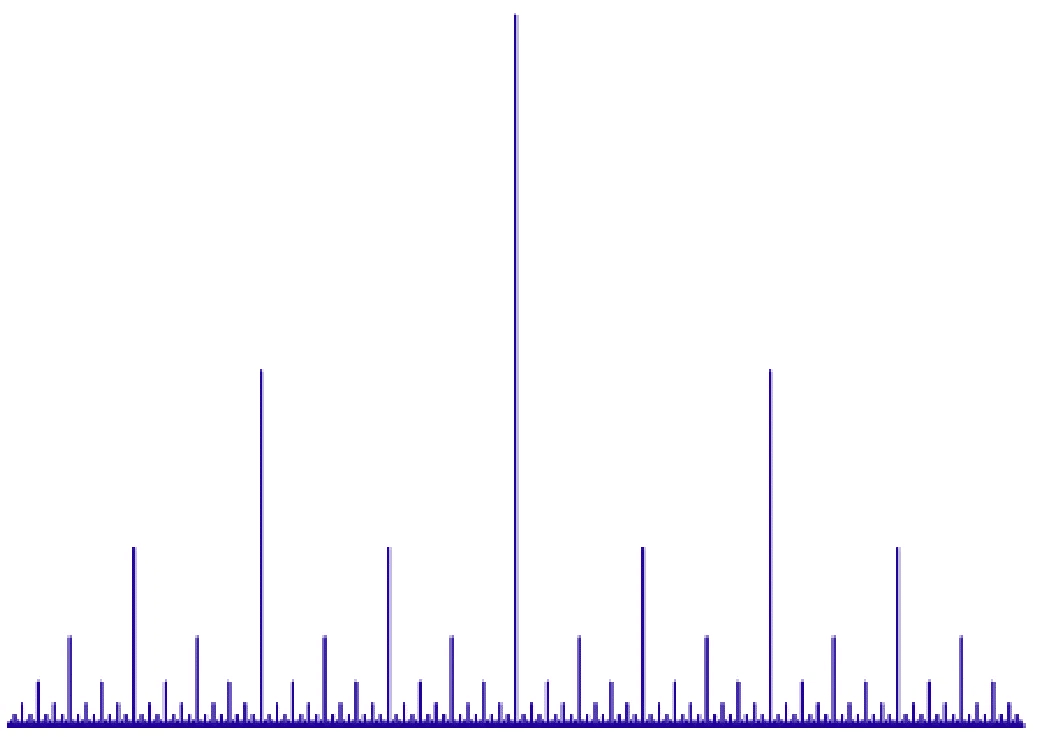
一旦B2aから離れて、様々なルールでのフラクタルを見ていきましょう。
B3/S23-a4ei6というルールには、以下のようなものがあります。

一見するとただのシェギャに見えますが、今までとは違い固定物体・振動子でなく移動物体がシェギャを構成しています。

もうシェギャ見飽きた?はいはい。ではシェギャのさらに発展版を見ていきましょう。
シェギャは、左の図形を右の図形に変換する操作を無限に繰り返して生成されます。

では、このような操作に変えてみるとどうなるでしょうか?
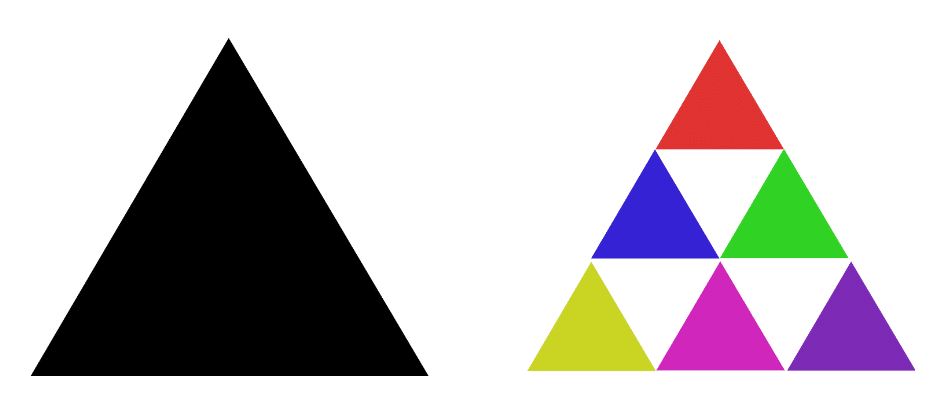
そのようなフラクタルを生成するパターンが存在しており、こんな感じになっています。


はい。こっから暴走します。これします。
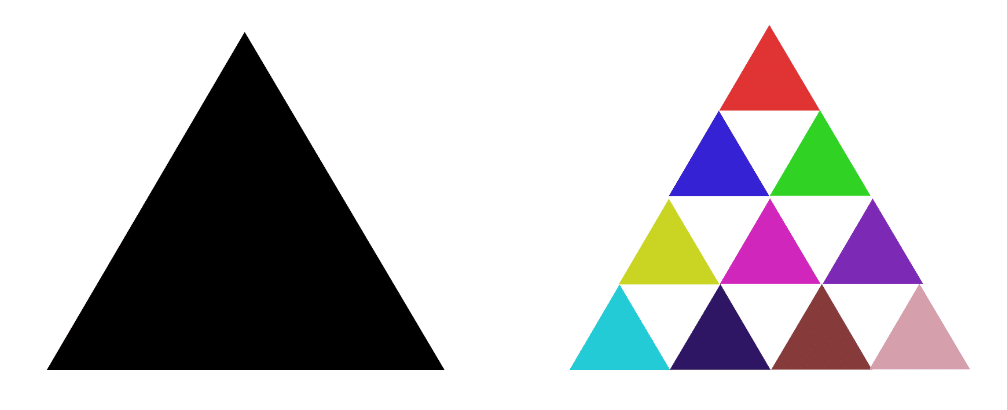


次?そろそろ色が尽きてきたので勘弁して。


ではなぜこのような模様が生成されるのでしょうか?
結論から言うと、これはReplicatorの挙動によるものです。上記3つのパターンはいずれも移動しながらReplicatorを生成していくもの、つまりB36/S23で見たアレと同じような原理なのです。
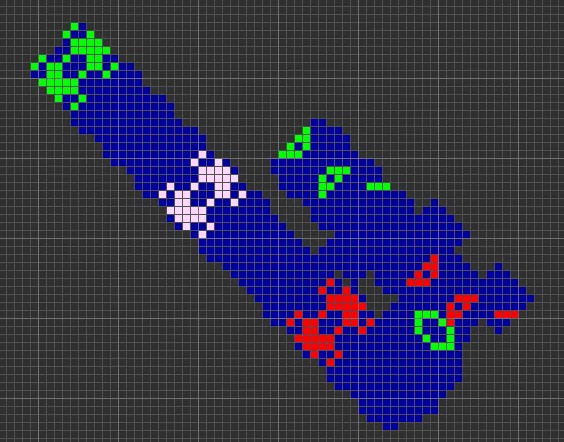
B36/S23やB2aei/S0ではReplicatorがルール90に従い動くのに対し、これらのルールでのReplicatorはまた別のルールに従っているため、結果的に異なる図形が生成されるんですね。
本当はこの続きの話、例えば複数状態のものや「周り」の定義を変えたものなど色々見たかったのですが、話のネタがありすぎてもう書ききれねえので次々回で続きをやります。だから読んで。
まとめ・次回予告
いかがでしたか?今回はセル・オートマトンについて紹介しました。
まず初めに。嫌ほどシェギャを見せてしまいごめんなさい。でもしょうがなかったんです。
フラクタルを生成する方法に、難しい関数の計算以外に視覚的に過程や仕組みが分かりやすいこんなものがあったなんて驚きですね。見てて楽しいし他の描画法とはまた違った魅力があります。またパターン自体とグラフ、両方を基にフラクタルを生成するという取り組みも行いましたね。
セル・オートマトンではこのように多面的な視点から見れることが多く、似たルールを見ることで別のフラクタルを見つけられるのも楽しいです。私は暇な時ルールを適当に色々変えて面白いパターンを見つけていました。受験生になるまでは。あー悲し。
次回は「ストレンジアトラクター」についてやります。クリスマスに投稿です。お楽しみに!!!!

参考
紹介したパターンの一部は以下から引用・参考にしました。
・Gollyの標準プリセットより、
「infinity-binary-ruler-generator.rle」
「Sierpinski-builder.rle」
余談
長い記事が多くて(私が)疲れましたね。26、27は軽めな記事になる予定です。(そもそも受験勉強があるから。)
なお、#26以降は2週間に1回の更新となってしまう予定ですが、第一志望の合格に向けて頑張っているので怒ったり恚ったり慍ったり嚇ったり噁ったり悁ったり愾ったり嗔ったり瞋ったり忿ったり馮ったり怫ったりしないでください。
次回の投稿クリスマスだから言わせて。
受験生には!モミの下でキスする一時も!君の手だけを熱源に白い道を歩く幸せも!!イルミネーションのように美しいあなたの頬を撫でる余裕も!!!ねーんだよ!!!!
サンタを垣間見ようと寝たフリするも結局寝てしまう、あの頃の純粋な心も!!来年こそは俺もあんな風に、なんて妬む心も!!!ねーんだよ!!!!
クリスマスプレゼント参考書と過去問だよ!!!ゲーム来ねえよ!!!
