
【フラクタル解説】FNFE Project #28「われても末に...」
挨拶
hhayyattoは2025年1月22日!!!15歳になりました!!!!!
15歳になったので、
➀民法961条…遺言をできるようになる
②児童福祉法34条…色々できるようになる
③国籍法…国籍の取得・離脱・選択が法定代理人に依らなくてもよくなる
④労働基準法56条…働ける
⑤公健法8条、25条…公健法で定められた指定疾病による障害の程度が政令で定める障害の程度に該当するものであるときは、当該被認定者の請求に基づき、公害健康被害認定審査会の意見をきいて、その障害の程度に応じた障害補償費を貰えるようになる
など色々なことができるようになりました。
まあ置いといて、15歳と言えば高校生。もう少しで高校生なので、この中3の時期に封印していたことを思いっきりやって高校生活を全力で楽しもうと思います!!!!!!(そのためには勉強しろ)
どうもこんにちは。FNFE Projectへようこそ!
FNFE Project「実戦」では、今までのフラクタルの基礎的・標準的な知識をベースに、より踏み込んだことについて探求・探究していきます。
さらには関わりの深いカオス理論・カオス力学系とも絡めながら最終的には複雑系への理解を深めていきます。
今回は「リアプノフ指数」「様々な一次元写像」「いろんな次元」をやります。頑張れ。
刺客は何時も死角から来る
リアプノフ指数というのは#23で軽く触れ、計算式も提示しましたが、詳しい内容については触れていなかったのでここで改めて説明しようと思います。
リアプノフ指数とは、一次元写像xₙ₊₁=f(x)がどのくらいカオスであるかを示す指数のことで、多くの場合はλで表されます。以下のような式で求められます。

式に極限が入っているので、普通はNをいい感じのところで計算してそこで計算を打ち切るという方式が取られます。
んじゃちょっと例を求めてみましょうか。パラメーターaが以下であるロジスティック写像について、そのリアプノフ指数を求めてみましょう。最初のxは全て0.1、N=1000000とします。
➀a=1.5 (1周期)
②a=3.2 (2周期)
③a=3.7 (カオス)
④a=3.9603 (4周期窓)
まず、ax(1-x)をxについて微分するとa(1-2x)となります。なのでこれを利用して式を立てればいいですね。
で、まぁリアプノフ指数は以下のようなプログラムで求められます。Nとaを指定すれば後は勝手に求めてくれます。

ということで求めるとこうなります。
➀$${λ≈-0.3010287…≈-log(2)}$$
②$${λ≈-0.3979351≈-log(2.5)}$$
③$${λ≈0.1539919}$$
④$${λ≈-0.2668623}$$
はい。こう見ると、いくつかの地点では正確なリアプノフ指数を求めることが可能なことがわかりますね。さらに試すと色々なことが分かります。

まず、2種類の図を重ね合わせてみました。
赤線がリアプノフ指数を縦軸に取ったもの、青いやつがロジスティック写像の分岐図です。灰色の線はλ=0の地点を示しています。
リアプノフ指数はカオスの度合いを表す指数なんですが、カオスでないところでは負の値、カオスなところでは正の値になることがこの図から分かります。
より分かりやすくするために、3.5≦a≦4の範囲を拡大して見てみましょう。
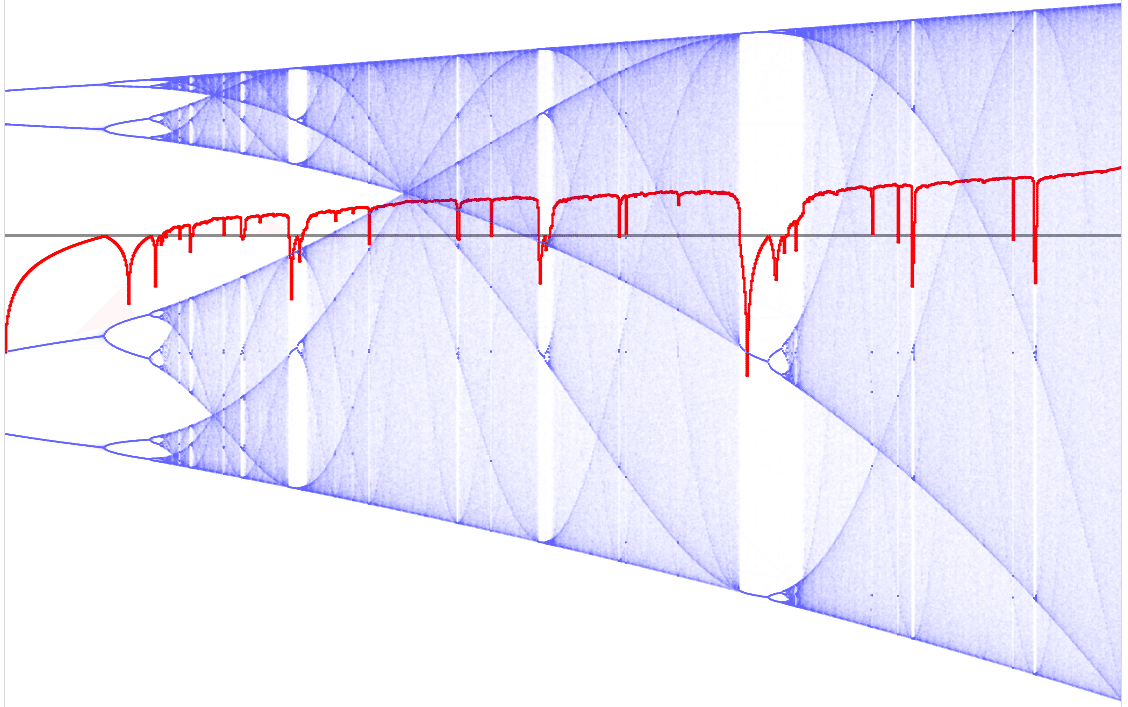
窓のところでリアプノフ指数が小さくなり、安定していることを表すマイナスになっていることがわかります。そして窓の終わりでは再びリアプノフ指数が大きくなり、やがてカオスを示す正に転じています。
リアプノフ指数の性質をまとめると以下のようになります。
・カオスの度合いを測る指数
・カオスではない→リアプノフ指数は負で、安定しているほど指数は小さい傾向
・カオスである→リアプノフ指数は正で、カオスが強いほど指数が大きくなる
他の一次元写像でも試し…え?誰こいつ?

???「やあ!ボクはテント写像だよ。僕はロジスティック写像とはお互い従姉妹同士の」
私「(囁き)なぁ、こいつ誰?」
解説おねえさん「(囁き)え?知らん。テント写像とか言ってるけど。まぁ喋らせるだけ喋らせとけ。」
テント写像「ボクはこんな定義の写像。パラメーターμを変えるとxの動きが変わる。」
$${x<\frac{1}{2}\cdots μx}$$
$${x\ge \frac{1}{2}\cdots μ(1-x)}$$
テント写像「そしてボクの姿が写像の分岐図。何か僕を見て気づかない?ねぇねぇ何か気づかない??」
私「ん~~~…あっ。窓ない?」
テント写像「そう。窓がないから、1<μ≦2の時はほぼ全ての初期値でカオスになるんだね~★
μの変域は0≦μ≦2だけど、ボクの挙動は2つに分けられて、
・μが1以下なら不動点に吸引され、
・μが1以上なら必ずカオスになるよ。窓はないし、周期軌道も反発的なものしかない」
私「へー。ちなみにリアプノフ指数のグラフは?」
テント写像「……初対面のくせに的確にコンプレックス突いてこないで。(相貌苦れて逃げていく)」

他の一次元写像ではこんな感じです。
・ax(1-x²) ※2.2≦a≦3

・a(x+1/x²) ※-1≦a≦1

・$${\frac{a}{x^3-x+1}-1}$$ ※1≦a≦4

俺らが1Dで満足すると思う?
リアプノフ指数の考え方は2変数以上の写像にも拡張することができます。
d次元のリアプノフ指数は次元ごとにそれぞれ$${e^{λ_1},e^{λ_2}...e^{λ_d}}$$と表され、以下のような計算式で求めることができます。

ただし、ここで$${E_M}$$は固有値の大きさ、J(xₙ)は$${\left( \frac{{\partial G_i}}{{\partial x_j}} \right)}$$というヤコビ行列です。
固有値とヤコビ行列の解説はおにいさんに丸投げします。よろ。
解説おにいさん「56す気か。まあ察せる通り引くほど難しいので頑張って聞いてください。
まず固有値とは、n次正方行列、つまりn×nという行列Aと零ベクトルでない列ベクトルx、つまり数を縦一列に並べたもの、それから複素数λに対して、Ax=λxとなるとき、λを固有値と言います。
固有値を求める方法を紹介しますが、その前にいくつかの用語を解説します。
置換…写像σ:X→Yが全単射で、始域と終域が等しいとき、この写像を置換と言います。
互換…置換のうち、2つの要素だけを入れ替えるものを互換と言います。置換は有限個の互換の積で表すことができます。
置換の符号…置換σが奇数個の互換の積で書けるならsgn σ=-1、偶数個の互換の積で書けるならsgn σ=1となります。これを置換の符号と言います。
行列式…n次正方行列A=($${a_{ij}}$$)とそれに対するすべての置換の集合Sₙに対して、以下を行列式と言います。det Aなどで表されます。

単位行列…n次正方行列のうち、行の番号と列の番号が等しい成分が1、それ以外の成分が0のものを単位行列と言い、Iₙで表されます。
$${\begin{pmatrix}1 &0 &0 \\0 & 1 &0 \\0 &0 &1\end{pmatrix}}$$←例えば、これはI₃です。
やっと解説できます。$${det(λI_n−A)=0}$$が成り立つλが、Aに対する固有値となります。めんどいですね。
続いてヤコビ行列なんですが、これガチでめんどいです。
まず、n変数関数f(x₁,x₂,x₃…xₙ)がk個あるという状態を考え、f₁(X),f₂(X)…fₖ(X)をそれぞれy₁,y₂,…yₖとします。ここで、各yᵢはxⱼで偏微分できるとします。
m×n行列で、$${\frac{\partial y_i}{\partial x_j}}$$をij成分とする行列をヤコビ行列と言います。写像の数は次元の数と同じですね。x=なんとか~、y=なんとか~、というようなイメージを持ってください。
で、N乗するとAになるそのような行列を求めて、それぞれの固有値を求めることで各次元のリアプノフ指数が求まるんですね。
じゃあ僕は帰りますバイバイ。」
一般に、リアプノフ指数のうち最大のものが正であればカオスと分かりますが、たまにリアプノフ指数が全部負でもカオスになるよく分からん奴があるので留意が必要です。
格子の講師
ここからは久しぶりに次元の話です。ハウスドルフ、ボックス、位相以外に何があるのでしょうか?ワクワクが止まりませんね。
まず、これから重要になっていくのが情報次元・相関次元です。これらは実はボックス次元の兄弟みたいなものです。
情報次元$${D_I}$$の定義はこんな感じです。

ここで、各変数にはランダムウォークが関わってきます。
・前提として、図形を格子で分割し、原点に置かれた粒子Pが各マスの中心を離散的に動くようにランダムウォークを行います。
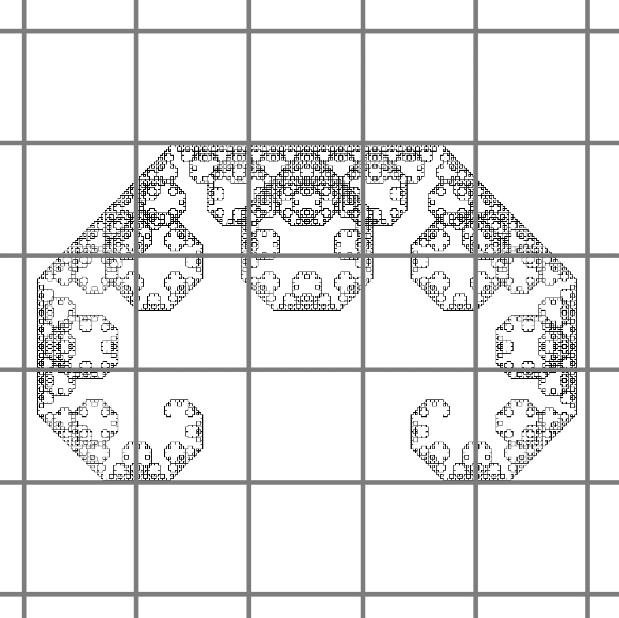
・nは図形上でランダムウォークを走らせた時の経過ステップです。
・$${S_n}$$は一度でも粒子Pがランダムウォークの過程で通過したマス目です。
・$${P_k}$$はk番目のマスを粒子Pが訪れる確率で、k番のマスを通過した回数を$${i_k}$$とすると$${P_k=i_k/n}$$で求められます。
続いて相関次元の説明です。これは2つ以上の漸化式からなるものに対して有効です。
求め方はこれです。

($${D_C}$$って言うのは適当に私が当てはめたものなので他のもので表されていることがあります。)
ここで、Mはフラクタルを構成している点の数、$${p_ε}$$は最寄りの点までの距離がεより小さい点の数です。
で、ボックス次元と今見た2つは、これから紹介するレニー次元の特別な場合と見なすことができます。これは以下のような定義です。
➀定数aと確率分布X=p₁,p₂…pₙを考える。
➁以下を求める。

③以下がレニー次元となる。

で、この確率分布はどう計算すればいいのかと言うと、プロットされた点x₁, x₂…xₙの集合がそのまま確率変数になるそうです。きついて。
また、多次元のリアプノフ指数を基にして考えられるフラクタル次元としてリアプノフ次元というものがあります。以下のような定義です。
➀リアプノフ指数を大きいものから順番に並べていき、順にλ₁,λ₂…λₙとする。
➁$${ζ_j=\sum_{k=1}^{j}λ_k}$$を求める。jは$${ζ_j}$$が負にならない最大値である。
③そのようなjが無い場合、リアプノフ次元は0である。
④系の次元の数kとjが等しい場合、リアプノフ次元はkである。
⑤$${D_λ=j+{\frac{\xi_{j}}{|\lambda _{j+1}|}}}$$がリアプノフ次元となる。
リアプノフ指数さえ求められたらすぐ求められるんですが、それまでの過程がめっちゃ難しいですね。
参考
井上義朗「力オス その定義と判定法」
井上純一「カオス・フラクタル 講義ノート #4」「カオス・フラクタル 講義ノート #9」
N. Pitsianis, G. L. Bleris, P. Argyrakis「Information dimension in fractal structures」
Alfréd Rényi「On Measures of Entropy and Information」
予告
スシローペロペロから早2年。まだ野生の皿は流れてきません。
醤油差しを舐める、他人の寿司に唾を付けるなどの行為をすると
・その後の人生
・株価
・株主の精神
が崩壊するので止めましょう。
代わりに僕の楽しい楽しい面白い面白い(反復の技法)記事を読んでください。受験前だけど変わらず書きます。
#29ではアーノルドの舌についてやります。文量があれだったら他の話を追加するかもしれませんが。

FNFE Project #29「¶甜」2025年2月5日。特色選抜当日に出す記事ちゃうやろ。
余談
なお、「相貌苦れる」というのはhhayyattoが考え付いた当て字だそうです。
プロセカの映画を2月5日に見に行きます。楽しみ
宣伝
2nd EP ”Chroma Records' Keywords„ (CRK)をリリースしました。
君を忘れまいと、乱雑にまとめられた記憶から思い出の瞬間を再構築するようなものでした。
もうすぐ私たちは真白に煌めく其々の場所へと旅立ちます。でも、未来は人それぞれと言っても、誰もが共にした思いもあるはずです。

