
【フラクタル解説】FNFE Project #14「キノコの縁」
どうもこんにちは。FNFE Projectへようこそ!
FNFE Projectでは「FNFE=For New Fractal Enthusiast(新たなフラクタル愛好家のため)」という理念の上、フラクタルについて分かりやすく解説していきます。
フラクタルについて全く知らなかったり、記事を読んだだけではなにがなんだかという人も楽しめるので是非読んでみてください!
今回は「ド・ラーム曲線」についてやっていきます。
知らない言葉が多すぎる
今まで色々な曲線を見てきました。高木曲線、レヴィC曲線、コッホ曲線、カントール関数、ミンコフスキーの疑問符関数。
一見するとそれらの曲線には共通点が無いように見えますが、実はあるひとつの曲線のグループに属するのです。
そのような曲線はまとめてド・ラーム曲線と呼ばれます。
下の画像に登場する曲線はド・ラーム曲線の例です。見たことあるやつばっかだと思います。

ということでここからド・ラーム曲線の定義を見ていくのですが、はっきり言って知らない言葉が多すぎると思います。後でちゃんと説明するので心配しなくても大丈夫です。
ド・ラーム曲線の定義
二次元ユークリッド空間上の完備距離空間Mとその上の2つの縮小写像の組D[0]、D[1]を考える。
xを区間[0,1]の実数とし、このxを以下のように展開する。

ただし、bₖは0か1のいずれかを適切に選ぶものとする。
さらにもう一つ写像cₓを考える。cₓは以下のように定義する。
cₓ=D[b₀]∘D[b₁]∘D[b₂]∘D[b₃]∘…(x)
このとき、cₓはM内のあるひとつの点pₓに収束していく。
xを[0,1]の範囲で動かしてプロットしたとき、pₓはM上にフラクタル曲線を描く。これがド・ラーム曲線である。
…?
知らない単語が多すぎますね。漢検準一級の問題文みたいな感じです。
凍解氷釈
というわけで一個ずつ解説していきます。
・二次元ユークリッド空間は歪曲したり曲がっていたりしない普通の平面です。私たちが見る普通の平面ですね。
・完備距離空間とは、簡単に言えば穴や隙間が開いていたりしない空間のことです。より正確に言えば、ある1点に収束する数列の収束先が必ずその空間に属する空間のことです。
完備距離空間でない例としては有理数全体の集合Qがあります。例えば、以下の漸化式の途中過程は有理数のみで構成されますが、最終的には無理数である√2に収束するため、Qは完備距離空間ではないとわかります。
$${a_{n+1}=\frac{1}{2}(a_{n}+\frac{2}{a_{n}})}$$
今回は複素数平面を二次元ユークリッド完備距離空間Mと見立てます。複素数zの実部はx軸に、虚部はy軸に対応しています。(複素数が分からない人は#7を見てもらえるといいと思います)
・縮小写像は以下のような定義です。
写像をf(x)、kを定数(0<k<1)、2つの点xとyの距離をd(x,y)としたとき、
d(f(x),f(y))≦kd(x,y)
を任意の点x, yで満たす写像を縮小写像と呼ぶ。
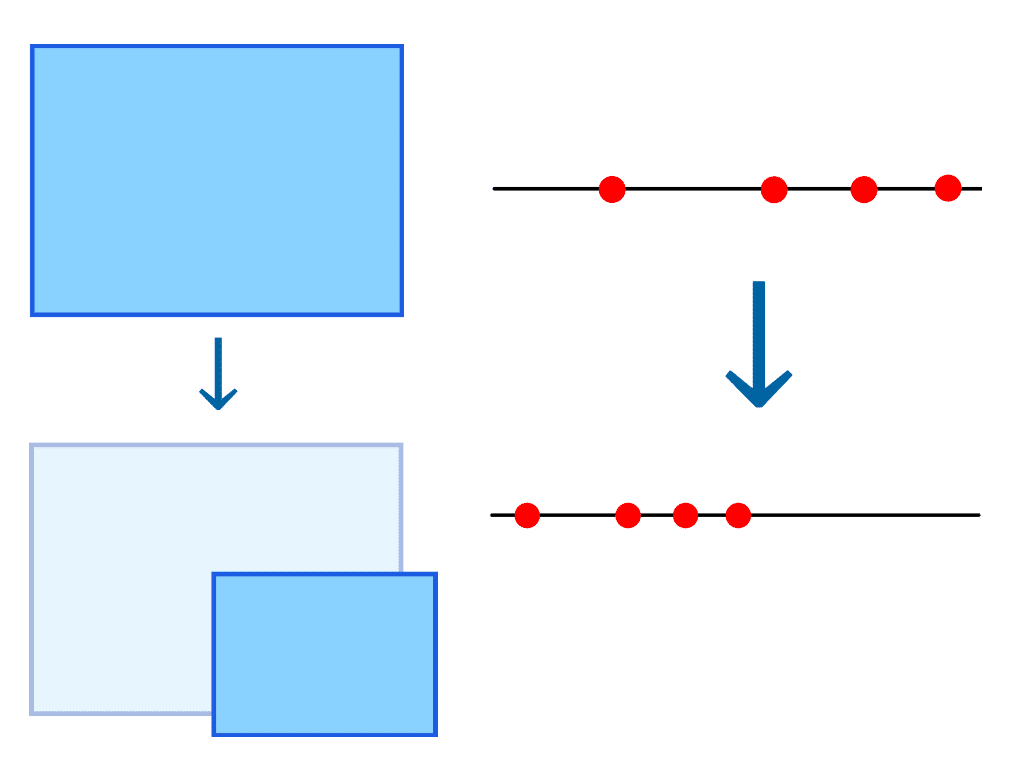
例えば、kを0.5とすると、「f(x)とf(y)の距離」より「xとyの距離の半分」の方が常に短くなるような写像f(x)、となります。
イメージとしてはこんな感じになります。

縮小写像には必ず不動点があります。不動点とは、変換を無限回繰り返したときに行き付く点のことです。そのような点をpₓと表しているんですね。
こういうのもどこかで不動点に辿り着くので縮小写像です。
Σは総和です。kを1から無限まで変えながら、$${\frac{b_k}{2^k}}$$を順番に足していきます。
∘は写像の合成を表す記号です。(g∘f)(x)=g(f(x))という感じになります。
3つ以上の写像を合成する時、順番は気にしなくてもよいです。つまりこんな感じです。
(h∘g)∘f = h∘(g∘f)
ただし、g∘f=f∘gとは限らないのでそこは注意が必要です。
ということで、今回用いる定義を分かりやすくまとめ直すとこのようになります。
ド・ラーム曲線の定義(令和最新版)
複素数平面上の2つの縮小写像の組D[0]、D[1]を考える。
xを区間[0,1]の実数とし、このxを以下のように展開する。

ただし、bₖは0か1のいずれかを適切に選ぶものとする。
さらにもう一つ写像cₓを考える。cₓは以下のように定義する。
cₓ=D[b₀]∘D[b₁]∘D[b₂]∘D[b₃]∘…(x)
ここで、∘は(f∘g)(x)=f(g(x))を意味し、左から順に計算していく。
このとき、cₓはM内のあるひとつの点pₓに収束していく。
xを[0,1]の範囲で動かしてプロットしたとき、pₓはM上にフラクタル曲線を描く。これがド・ラーム曲線である。
随分わかりやすくなりましたね。(多分)
春宵一刻
ということで!!!!!ここからは色々なド・ラーム曲線を見ていきます。
ド・ラーム曲線にもいくつか分類がありますので、一つひとつ順番に見ていきます。
まず初めに見るのはチェザロ曲線(Cesàro curves)というものです。
チェザロ曲線はド・ラーム曲線のうち、D[0]とD[1]の定義が以下のようになっているものです。
D[0](z)=az
D[1](z)=a+(1-a)z
ここで、aとzはどちらも複素数を表し、|a+bi|=$${\sqrt{a^{2}+b^{2}}}$$としたとき|a|<1、|1-a|<1となります。
a=0.5+0.5iのとき、チェザロ曲線はレヴィC曲線の形となります。

a=0.3+0.3iの場合はこんな感じです。キノコの縁のようですね。

a=0.2+0.4iの場合はこれです。タコやん。

ところでみなさん、これどこかで見たななんて思いませんでしたか?

そうです。#3でやりましたね。これらの曲線は、ピタゴラスの木という図形の先端部分に相当します。

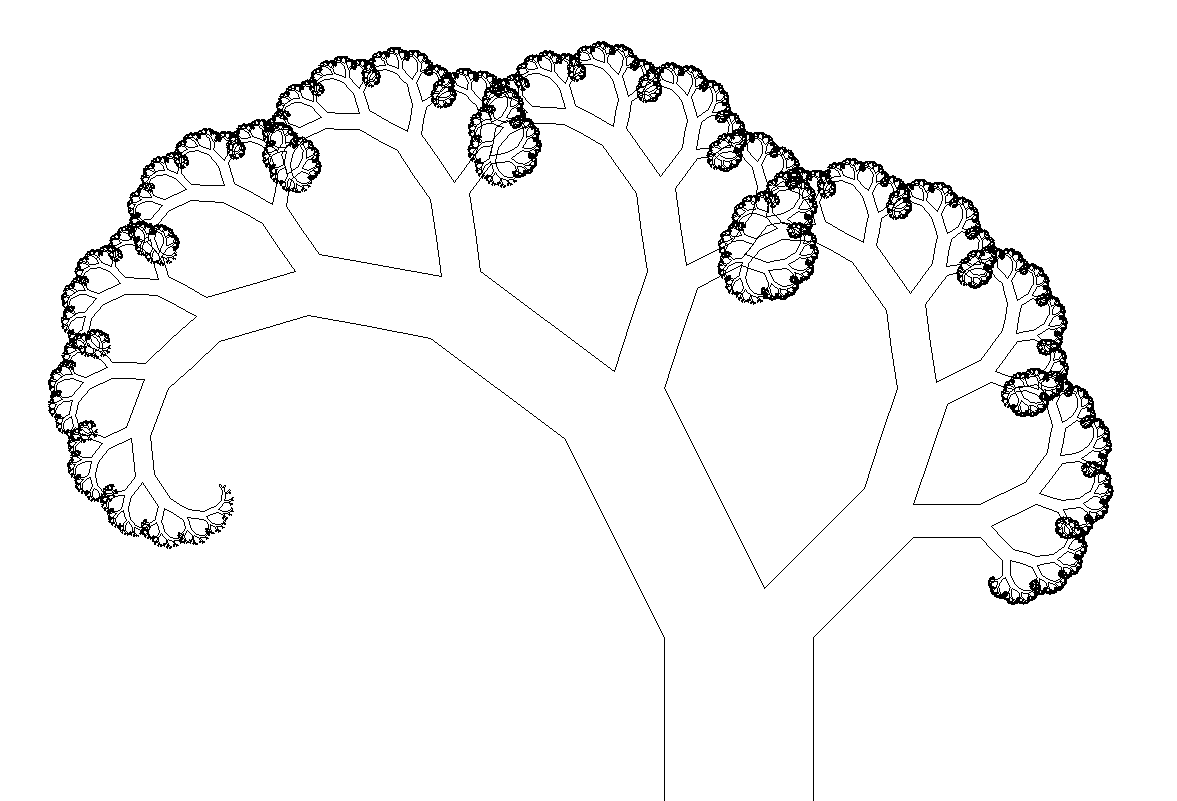

ピタゴラスの木とは、このような手順で生成されるフラクタル図形です。

あるいは、正方形ではなく長方形にすることもあります。

こうやってできた図形の先端部分がチェザロ曲線となるわけです。#3らへんのことを完全に忘れかけているという人は#2-4くらいを一回読み直してきてください。
忘却曲線
続いてはコッホ=ペアノ曲線についての紹介です。
コッホ=ペアノ曲線は、D[0]とD[1]が以下のような定義のド・ラーム曲線の総称です。
D[0](z)=az̄
D[1](z)=a+(1-a)z̄
※z̄はzの複素共軛
はい。コッホ=ペアノ曲線の式は、チェザロ曲線の式のzに共軛な複素数を求める動作を追加したものです。
ということでコッホ=ペアノ曲線を見ていくのですが、その前に色々復習をしておきます。
まずコッホ曲線はこれです。

構成としてはこんな感じになっています。

懐かしいですね。
次にペアノ曲線がこれなんですが、実はこれには一つ注意点があります。

それは、このペアノ曲線は仮の姿であるということです。本来の姿を描こうとすれば、たちまちこうなってしまいます。

こうなるのはペアノ曲線が空間充填曲線だからです。
※あなたの習ったペアノ曲線と違うと思いますが、どうもペアノ曲線という言葉は2種類の空間充填曲線を指すようなので、#5の記憶は一旦消してください。
復習です。空間充填曲線とは、特定の空間全体を通る曲線のことです。
本来の空間充填曲線とは一定の範囲内のすべての地点を通る曲線なので、どうしてもあのような形になってしまいます。そのため空間充填曲線を描くときは基本的に図Aのような描く途中過程を掲載します。
a=0.5+$${i\frac{\sqrt{3}}{6}}$$のときはコッホ曲線が出てきます。

a=0.5+0.5iのときはペアノ曲線が登場します。

では虚部が$${\frac{\sqrt{3}}{6}}$$(≈0.2887)と0.5の中間のときはどうなるのでしょうか。



なんかすごい図形が現れました。
ここで登場している図形は、オスグッド曲線と呼ばれる曲線と酷似しています。
オスグッド曲線は、一つの大きな二等辺三角形から再帰的に細長い二等辺三角形を取り除いてできる曲線です。取り除かれる二等辺三角形の面積は、ステップが進むごとにどんどん小さくなっていきます。
この図形は「面積がある曲線なのに空間充填曲線ではない」という奇妙な特性があります。
一方で、視覚的にはオスグッド曲線と似ているものの、図Cは面積がありません。オスグッド曲線は三角形から有限の面積の一部を取り除いてできる図形なのに対し、図Cはあくまでも一本の曲線だからです。
不思議ですね。
なお、aの実部を0.5以外にすると…



なんかすごいことになります。
創
ここからは一般的なアフィン変換についてのド・ラーム曲線について解説していきます。
一般アフィン変換のド・ラーム曲線は、D[0]の不動点が0、D[1]の不動点が1の写像を持つド・ラーム曲線のことです。
Wikipediaが余りにも怪文書だったので自力で論文を解読したのですが、概して以下のような内容のようです。
一般アフィン変換のド・ラーム曲線の定義
今まで見てきたzやaを、z=u+iv, a=α+iβとする。
以下のような写像の組によるド・ラーム曲線を、一般アフィン変換のド・ラーム曲線とする。

行列なんて#8以来なので計算方法を解説します。
m×n行列Aとn×q行列Bの積のi行目、j列目の成分をcᵢⱼとすると、以下のようになります。

これは「Aのn行目のそれぞれの成分とBのn列目のそれぞれの成分の積の総和」という意味になります。
ということで実際に計算します。👆の式をあてはめるとこうなるので、

D[0]はこうなり、
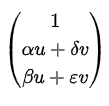
D[1]はこうなります。

ここで、元々uとvだった部分がまた新しいuとvになるというわけですね。
このα, β, δ, ε, ζ, ηを自由に変えられるのが一般アフィン変換のド・ラーム曲線、というわけなようです。
ということでこれも実際に図示してみ…たかったのですが!!!!!!
コーディングがうまくいかなかったので、今回は出すことができません。申し訳ございませんでした。
画像を見てみたいという人は、「参考にしたサイト(など)」の欄の2つ目のところを見てもらえるといいかなと思います。許してください。
またコーディングがうまくいき次第画像を出そうと思います。許して。
20240909追記:
完成しました。画像集はこちらから。
瑕疵
最後にWikipediaにダメ出しして終わろうと思います。
ミンコフスキーの疑問符関数が以下の写像のペアでできるとか書かれてますが、これ間違いです。
D[0]=$${\frac{z}{z+1}}$$
D[1]=$${\frac{1}{2-z}}$$
正しくは以下のようになるようです。
D[0]=$${\frac{z}{z+1}}$$
D[1]=$${\frac{1}{z+1}}$$
しかも、これで生成されるのは疑問符関数?(x)そのものではなく、?⁻¹(2x)が生成されるようです。
何をどう間違えたのでしょうか。。。
まとめ
いかがでしたか?今回は「ド・ラーム曲線」について解説しました。
チェザロ曲線ではピタゴラスの木、コッホ=ペアノ曲線ではコッホ曲線やペアノ曲線など空間充填曲線やオスグッド曲線などと色々関わりがあることが分かりました。
初期の頃の話が何個も出ていましたね。忘れかけているという人は初期の頃の復習をしておくと良いでしょう。
あと孫引きはやめましょう。ろくなこと無いです。
参考にしたサイト(など)
👆途中から信じない方がいい。
https://linas.org/math/de_Rham.pdf
👆画像がいろいろ乗ってる。
次回予告
解説おにいさん「お前石垣島でダイビング行ってきたんやろ?」
ぼく「シュノーケリングな?」
解説おにいさん「そうなんや。ってことはサンゴ見たんか?」
ぼく「見たで。」
解説おにいさん「あんな、サンゴってフラクタルやねん。」
解説おねえさん「あと雷と地衣類となんかもうその他諸々も。」
次回!!!!!拡散律速凝集!!!!!9月15日をお楽しみに!
余談
私は受験生なんですが、こんな記事ばっかり書いていていいのでしょうか。こんな事ばっかりしていて良いのでしょうか。日々懊悩しております。
