
【フラクタル解説】FNFE Project #29「¶甜」
どうもこんにちは。FNFE Projectへようこそ!
FNFE Project「実戦」では、今までのフラクタルの基礎的・標準的な知識をベースに、より踏み込んだことについて探求・探究していきます。
さらには関わりの深いカオス理論・カオス力学系とも絡めながら最終的には複雑系への理解を深めていきます。
今回は「アーノルドの舌」を解説します。
舌端
まずはアーノルドの舌を見てみましょう。以下の図における黒い部分がアーノルドの舌です。

???????
よく分からないですね。というわけでまずは前提知識を解説していきます。
カギとなってくるのが円周写像です。これは円周C上のある点aを別の点bに移し替える写像で、定義は以下のような感じです。
$${θ_{n+1}=θ_n+\Omega-\frac{K}{2π}\sin(2πθ_n)\mod 1}$$
ここで、0≦θ≦1であり、θは偏角として捉えて貰えればいいと思います。
円周写像にはΩとKという2つのパラメーターがありますね。この写像は元々ある電気回路をベースとして考えられたもので、Ωは外部から干渉する周波数を、Kは非線形性の強さを表します。
実際にΩとKを色々変えて、θの変化を見てみましょう。初期値は全て0.827です。私は暁山瑞希が好きなので。(倒置)

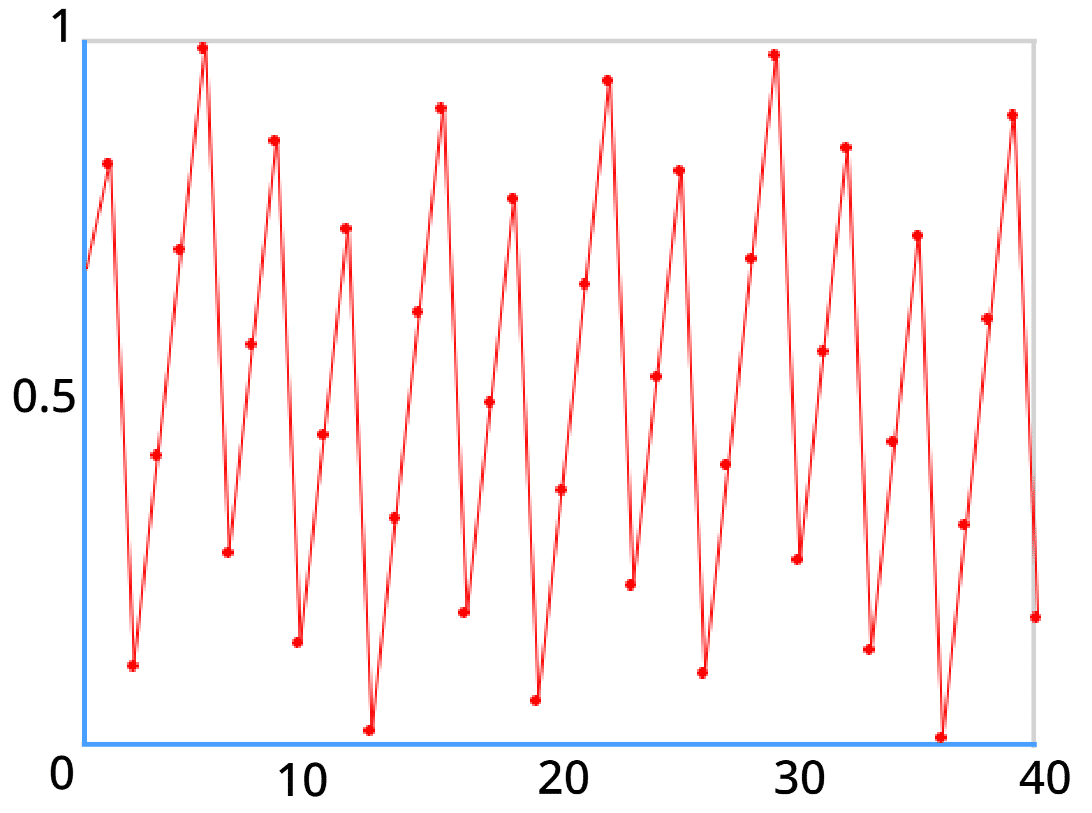

θは偏角なので、なんか回転してるっぽいのは伝わりますね。
ちなみにこの円周写像なんですが、ロジスティック写像の時と同じようにどの点を取るかをプロットするとこうなります。なんですかこれ。



舌尖
ここからが本題です。もうマヂ無理…と思えてきているかもしれないですがそろそろ定義が分かるのでついてきてください。
まず、ΩはMap Winding Number(写像回転数)とも呼ばれ、初期値がθの写像f(θ)の写像回転数W(θ)は以下のように定義されます。
$${W(θ)\equiv \lim_{n \to ∞} \frac{f^n(θ)-θ}{n}}$$
このfは$${f(θ)=θ+\Omega-\frac{K}{2π}\sin(2πθ)}$$とします。modがなくなっていますね。
で、この場合のW(θ)はΩと一致し、Ωが有理数である場合W(θ)は$${Ω=W≡\frac{p}{q}}$$と表現できます。
Kが0でない場合、Ωが有理数であるならばθは周期的な軌道となりますが、Ωが無理数の場合軌道は準周期的です。
しかし、KとΩが良い感じの値である場合、Ωが無理数であっても軌道が周期的であることがあります。この状態をMode Locking(モード同期)といいます。
さて、Kを縦軸に、Ωを横軸にとって、モード同期をする領域をプロットすると、K=0の測度0の集合からK=1の有限幅の集合まで領域が広がっていくのがわかります。領域のうち、有理数を取り囲む無理数のΩの集合をアーノルドの舌といいます。やっとわかりましたね。きつかったです。
ちなみにΩを固定してθ₀とKを動かすとこのようになります。横軸がθ₀、縦軸がK(0≦K≦4π)ですね。以下の図ではΩ=1/3で固定されています。

分岐図みたいで面白いですね。
₃なぁぜなぁぜ³
で、なんでこんなことが考えられているのかって言うと、そらもちろん現実世界と関係しているからです。
この円周写像というのは実は位相同期回路という回路をモデル化したものだそうです。
私は電気工学がさっぱりピーマンなので大雑把な説明しかできないのですが、この回路は入力された信号と出力する信号の位相を同期させる回路で、外部から加わる力と振動数からどのような挙動がするのか決まるようです。
そして一定の条件を満たすと同期して、その点をプロットしたときに同期を示す領域がアーノルドの舌らしいです。
ただ私は電気工学マジで知らないので適当なこと言ってるかもしれません。この部分は深く信じず流してください。
参考
https://www.hk.k.u-tokyo.ac.jp/kori/papers/seibutsu_rhythm_chap1.pdf
予告
これは私たちの経験する最後の試練で、今までの知識がすべて必要になるかのような単元です。
#30と#31を読むにあたり、今までの記事を完全に理解しなくてもいいので読み直しておくことをお勧めします。
この場所で私たちは過去の私達自身とすれ違い、時には歓び合い、時には無駄な忿恚に嵌るでしょう。
でも、最後に私たちは何かに結びつきます。それはフラクタルの全てを記述できる理論かもしれないし、何故現実世界の要素があの形なのかを理解する手掛かりとなるかもしれません。
FNFE Project #30 「鸞翔鳳集」。2025年2月19日。

余談
私立・特色の入試が終わりました。2月13日が楽しみです。
プロセカの映画を観に行きました。ニーゴのアフターライブ最高でした。暁山瑞希とその唄声を映画館の大画面大音量で見聞きできただけで僕は人生幸せです。
