
【フラクタル解説】FNFE Project #11「炎上艢舫」
※艢・・・ショウ・ほばしら。船に帆を張る柱。マスト。
舫・・・ホウ・ふね・もやいぶね・もやーう。二隻並べて繋いだ舟。舟を繋ぐ。
題名の読み方は「えんじょうしょうほう」でお願いします。
注意!!!集合体恐怖症じゃなくてもきつい画像があります。
どうもこんにちは。FNFE Projectへようこそ!
FNFE Projectでは「FNFE=For New Fractal Enthusiast(新たなフラクタル愛好家のため)」という理念の上、フラクタルについて分かりやすく解説していきます。
フラクタルについて全く知らなかったり、記事を読んだだけではなにがなんだかという人も楽しめるので是非読んでみてください!
今回は「バーニングシップ・フラクタル」「マルチブロ」などを解説していきます。
iの復讐
#7「閉月羞花」はもう読みましたか?読んでいないという人、あるいは忘れてきたという人のためにこの章で軽く虚数とマンデルブロ集合について説明しておきます。
・虚数とは
2乗すると-1になる数を考えます。普通はそんな数は存在しませんが、無理矢理存在させます。このような数をiと表して虚数単位と呼びます。
a, bを適当な実数としたとき、a+biの形で表される数を複素数と言います。複素数同士の演算は、こんな感じで行います。

数直線上で数を表すように、複素数たちは平面上に表されます。これを複素数平面と言います。(複素平面・ガウス平面と呼ぶこともあります)
・マンデルブロ集合について
マンデルブロ集合とは、以下のような漸化式を計算したときに発散しないような複素数cの集合です。
zₙ₊₁=zₙ²+c
z₀=0
・ジュリア集合について
ジュリア集合とは、複素数cを適当に決めて、以下のような漸化式を計算したときに発散しないz₀の集合のことです。
zₙ₊₁=zₙ²+c
炎上してる
というわけで今回はマンデルブロ集合・ジュリア集合等エスケープタイムフラクタルに詳しい才木珠莉亜ちゃんと一緒に見ていきます。よろしくお願いします。

というわけで!!!まずはバーニングシップ・フラクタルを見ていきます。
バーニングシップ・フラクタルとは、以下のような漸化式を計算したときに発散しないような複素数cの集合です。
zₙ₊₁=$${(|Re(zₙ)|+i|Im(zₙ)|)²}+c}$$
z₀=0
このReとImの意味は、複素数zₙの実部と虚部、つまりa+biのaの部分とbの部分を表しています。Re(a+bi)=aで、Im(a+bi)=bということですね。また、|a|はaの絶対値を表します。
マンデルブロ集合の式と比較してみましょう。
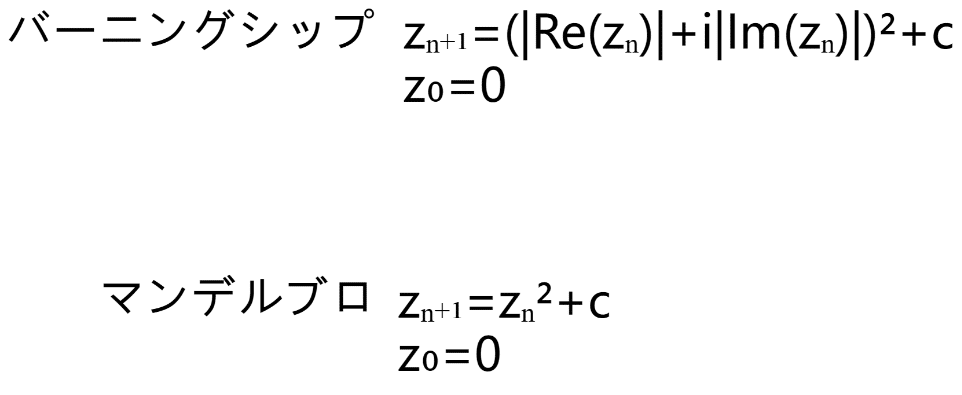
バーニングシップフラクタルの式は、マンデルブロ集合の式に加えて、zₙを二乗するときに実部と虚部をそれぞれの絶対値に変える、という動作が入ります。
マンデルブロ集合を複素数平面上にプロットできたようにバーニングシップフラクタルも複素数平面上にプロットすることが出来ます。さあ!!!どんな見た目になるでしょう!!!!
ヒントは、その名前です。

ということで正解発表です!答えは、、、こちら!

※基本的に上側が正となっている画像のi軸は、今回は負になっています。これは慣例によるものです。この記事ではこれからも画像は上下反転させて表します。
…船っぽくないじゃねえか!!!騙しやがったな!??!?!と思った方もいるかもしれません。しかし一旦落ち着いてください。左の方になんかありますね。そこを拡大するとどういうことか分かります。

色のせいかもしれませんが、なんか燃えて倒れかけてる船っぽいやつが見えますね。焼け落ちて傾いた帆柱のようなもののも、壊れかけた船首らしき部分も見えます。黒と黄色の混じったモザイク状のノイズも燃え滾る煙を演出しています。めちゃくちゃ船でしたね。
もう少し左側にあったやつはもっと豪い燃え方をしていました。

色々バリエーションがありますね。バーニングシップフラクタルもマンデルブロ集合と同様、それぞれの小さい奴らはお互い異なった形をしているようです。

コピーが小さいほど、伸びている帆柱は船本体のサイズに対して長くなるようです。

ちなみに…

この辺りにもヤツがいます。

一番上の青枠を拡大するとこんなものがあります。

それをさらに拡大するとこんなものが表れます。

バーニングシップフラクタル本体と似たような図形が現れました。
こうして見ると我が子を大事そうに護(まも)る生物のように見えてきて神秘的なものを感じますね。(俺だけ?)
多角的超えて多胞的な視点
珠莉亜ちゃんがなんか言いたそうにしていますね。なんでしょうか。

(珠莉亜)いや~~、、、バーニングシップフラクタルって船のところだけ注目されがちじゃん?だから他のところも見てほしくてさ。
(ぼく)確かにそうですね。バーニングシップフラクタルを拡大する動画を見てみると、その大半が左の方を拡大していて残りの部分は全然注目されないでいます。ということで各部分に名前を(勝手に)付けたので色々見ていきましょう。
ちなみにさっき見た船のところを私は「舫(もや)い船領域」と勝手に呼んでいます。
※ここから先しばらくは、ウィキペディアガチ勢が見たら卒倒するほどの独自研究と画像ラッシュです。
まずは画像中央部にある、スポンジ状の領域を見ていきます。私はここを勝手に「泡状領域」と呼んでいます。

拡大しても、ずっとこのような不規則な泡状構造が続いていて、正直あんまり面白くありません。

たまに余りにも歪みすぎていてもはや本体と類似形とは言えない図形が出てきます。

他にもエイのような形の領域が現れることがあります。

関係があるのかは知りませんが、バーニングシップの右上あたりにはエイ領域に酷似した領域があります。

泡状領域と舫い船領域の境目はこんな感じになっています。なんかもう凄いごちゃごちゃしていますね。

泡状領域同士の隙間には黒い領域が全くと言っていい程現れない領域があります。

続いては右上の領域を見ていこうと思います。私はここを勝手に桟橋領域と呼んでいます。(船になぞらえるん好きやな~~~)
この辺りは飛び地の種類も密度も多くて個人的に好きな領域です。

このように偽コッホ雪片みたいなのが連なっています。各所各所に飛び地が見られます。

桟橋領域で見られる飛び地には色んな形があります。大きく4つの形に分けられるようです。ただしこれらの特性がいろいろ混じったような変な図形が出ることもあるので一概には言えません。

泡状領域と桟橋領域の中間地点は緩やかなグラデーションを描いて遷移するのですが、その辺りでは結構エイ形の飛び地が多い気がします。

また面白いことに、マンデルブロ集合では見られなかった完全に本体と繋がっていない領域も見られます。

こんな感じのまばらな塵のような領域も見られます。拡大すると黒領域が現れるものと拡大しても現れないものの2つに分けられます。(法則は謎です)

飛び地を調べていると褶(しゅう)曲した地層のような縞模様が見られることがあります。飛び地に近付くにつれ、まるで重力レンズに歪んでしまった光のように曲がって周りの模様が見えてきます。

この辺りを拡大すると、引き伸ばされすぎて何が何だか分からなくなってしまった飛び地が見られることがあります。

飛び地において舫い船領域に相当する領域はもはや無法地帯です。分類不可能な形の飛び地がたくさん見られます。

燃えている船の先端だけが抜け落ちてここにポツンと現れたみたいな形です。

なんか融合しています。

なにこれ?(ジュリア集合でも似たようなのが現れていた気がします。)

右下にもなんかあります。ここは適当に衝角領域と呼んでいます。

なだらかな線状になっているところは拡大しても面白くありませんが、モザイク状の領域があるのでそこを拡大してみると、、、

泡状領域と似たような構造が出てきます。
謎の形です。

この辺りは拡大してもあんま面白くないし描画にも異常に時間かかるしで個人的に好きではありません。
バーニングシップフラクタルには三か所なんかヤバいくらい引き伸ばされた地形がみられる場所があります。左から見ていきます。

左はこんなことになっています。飛び地も見られることがあります。(黒い四角は描画の不具合によるものです)

この辺りの飛び地は細長い円盤状であることが多いです。

そこからちょっとx軸に沿ってプラスの方向に移動するとこんなエリアがあります。このエリアでは、黒領域が引き伸ばされに引き伸ばされ、完全に縞模様と同化してしまっています。

こんな感じ。実際はこれの数十倍、下手したら数百倍は長いです。

細長い黒領域の先端はこんな感じになっています。(補正してあります)

真ん中の矢印はエグい飛び地が大量発生しているエリアです。

拡大するとこんな感じになっています。

右上の方に近付くとこんな感じになっています。

この時点で既にヤバイ飛び地が大量発生しています。

この辺りで見られる飛び地は異常に引き伸ばされていて形が謎だったのですが、多分基本はこれだろうという形を見つけました。



この辺りではモザイク自体が飛び地として表れることもあります。

右端の矢印で示した領域を見ていきます。ここは桟橋領域に近いところにあります。

本体とある程度離れているような地帯では、このようなシミ状の発散領域があって、その中央に黒領域が鎮座(?)するみたいな形がよく見られます。


大量の飛び地がくっつくかくっつかないかの瀬戸際で発生していることもあります。

また、このような模様が見られることがあります。

これはカントールの塵と呼ばれる図形に似ています。

本体に近い領域では、先ほど見たような細長い黒領域が見られます。

この細長い黒領域の先端にはどうやら3つパターンがあり、
・先端が複雑に分かれている「ささくれ形」
・先端がはっきりしている「ペン先形」
・先端が非常に細く長く伸びる「針形」
に分けられるようです。

個人的には、ささくれ形は本体から離れたところ、針形は本体にかなり近いところ、ペン先形はその中間に多いイメージがあります。
ということで、バーニングシップフラクタルのあらゆるところを見てみました。正直自分でも知らなかったこともあったのと、景色のバリエーションがマンデルブロ集合の何倍も豊かだったので楽しかったです。
kを弄ぼう
この時点で既に4000文字以上と厖大(ぼうだい)な量の画像を見てきてつらいかもしれませんがまだ続きます。
続いてはマルチブロについて紹介していこうと思います。
マルチブロとは、マンデルブロ集合の漸化式を以下のように変えてできるフラクタル図形のことです。

式を見て分かる通り、kが2のときは通常のマンデルブロ集合に対応します。
kを変えてみて形の変化を見てみましょう。
※以降、次数がkのマルチブロを「kのマルチブロ」と呼ぶことにします。




という感じです。
マンデルブロ集合が点対称にくっついたような変な形をしています。一般的に、マルチブロは(k-1)回回転対称のようです。
またkが偶数の時はマンデルブロ集合やバーニングシップフラクタルで見られた左に直線的に伸びる構造が確認できます。

マンデルブロ集合では見られないような位置に切り込みが入っていることもあります。この画像では、中央上部のような谷状領域はマンデルブロ集合では見られない形となっています。

基本的なつくりはマンデルブロ集合と似ていて、拡大すると類似した構造を確認できます。



ここで、kを小数にするとどうなるのかという疑問を持った人もいると思います。

正直できるっちゃできるんですけど、なんか不自然なところが出来てしまうので基本的には避けられるというのが現実です。
例えばこれはk=2.5の場合です。

拡大してみるとわかるのですが、不自然に途切れた部分や本体と繋がっていない部分、歪んだ領域などが発生して不自然な形になっています。

他にもバーニングシップフラクタルで見たようなモザイク状の領域も発生してなんかよく分からない状態になってしまいます。

不整合の極みにはこんなものがあります。マジで無加工ですよ。
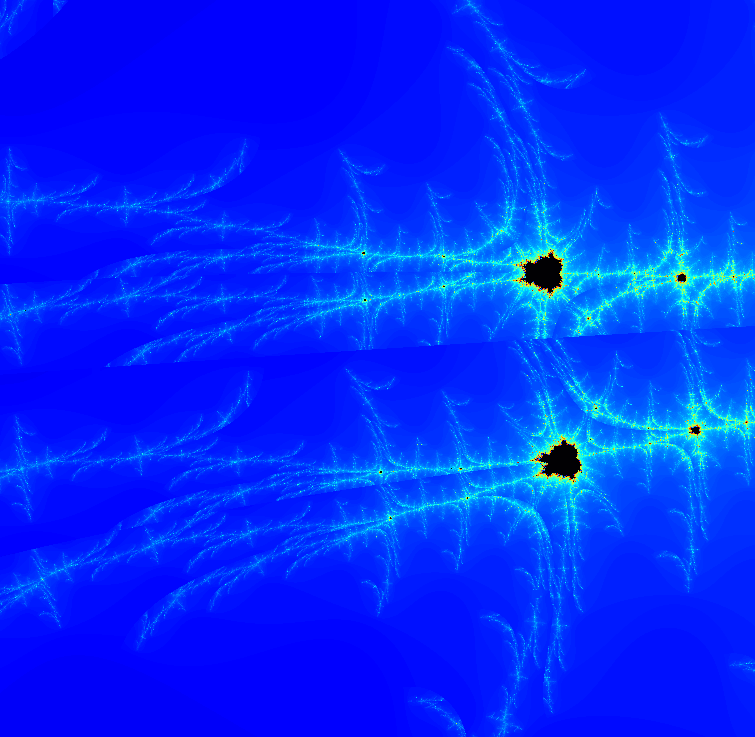
kが小数の時は、kに近い整数のマルチブロと似たような形が見られることがあります。


ちなみにkを1にするとマルチブロには原点しか属さなくなります。zₙ₊₁=zₙ+cという式は言い換えたらcを無限回足すってことになるからですね。
kはマイナスにもできます。が、なんかマジで意味不明な形になります。

収束する領域、発散する領域、ノイズ状の領域が最高に気持ち悪く混ざり合ったヤバい図形が現れます。しかしこれ以外にめぼしい物は現れません。

なのでkがマイナスの場合もほぼ論じられません。
coupling isn't always nice
ここまで見てきて「マンデルブロ集合に対してジュリア集合があるように、バーニングシップフラクタルやマルチブロにもジュリア集合的なやつがあるんじゃね?」と考えられていた人はいい視点で読めています。

実はジュリア集合っていうのはマンデルブロ集合の対に限った概念ではなく、fを適当な関数や変換としたときzₙ₊₁=f(zₙ)が無限大に発散しない初期値z₀の集合の事を言います。(正確には違うらしいですが皆これで通しているので多分大丈夫です)
ほなはよ見せろやって意見が出ると思いますが、

とのことです。
知らん。いいから見せろ。っていう意見が出てきそうなので早速見ていこうと思います。まずはバーニングシップフラクタルのジュリア集合から。




・・・つまんねぇぇぇ~~~。。。
見た目も地味ですしバリエーションもあんまないしフラクタルっぽさもあんまないしで酷いですね。ただマンデルブロ集合のジュリア集合とは違う性質があって、

ジュリア集合の黒領域同士が離れていたり、


バーニングシップフラクタルに属していないcを選んでジュリア集合を描いても、黒領域が現れたりすることがあります。(ただし、バーニングシップフラクタルに属していないcでジュリア集合を描いた時、原点がジュリア集合に属さないというのは共通しています)
バーニングシップフラクタルのジュリア集合は、縦と横の軸に線対称になるようです。
続いてはマルチブロのジュリア集合を見ていきます。





めちゃめちゃきれいやん。何やったんさっきの地味そうなムーブ。
kのマルチブロのジュリア集合は、k回回転対称になるようです。またマルチブロのジュリア集合は黒領域同士が離れ離れにならず、マルチブロにおいて黒領域に属するcのみ黒領域が現れるようです。
ちなみにバーニングシップフラクタルのマルチブロ版みたいなやつは…


え?

お前誰?


誰だよこいつら…

ジュリア集合はバーニングシップのジュリア集合と似すぎてて全然面白くなかったです。
まとめ
いかがでしたか?今日はバーニングシップフラクタルとマルチブロについて解説しました。
マンデルブロ集合の式を少し変えてみると、模様も性質も何もかも違ってくるなんて面白かったですね。自分でも知らなかった面が見えてきたので調べていて楽しかったです。物事というのは多角的に捉えるのが大事だとよく分かりました。
またバーニングシップフラクタルやマルチブロのジュリア集合も見ました。習ったことを融合させて新しいことを考えてみる、中々大事なことだと思いますよ。これからも今まで学習したことを土台にして、さらに発展的なことをしていくので頑張りましょう!
次回!「ロジスティック写像」!!!!!お楽しみに!!!!!!!!!!函菜ちゃん推し(いるの?)にはたまらない内容だと思います。(8/27更新です。ちょっと間が空きますが、僕の大好きなキャラの誕生日なので内容に気合いが入ってると思いますw)
参考にしたサイト
※ジュリア集合・マンデルブロ集合の画像は「Fractal Zoomer」というソフトウェアで描画しました。それ以外の画像はパブリックドメインのものか自作です。
余談
バーニングシップフラクタルがテーマの記事は元々8月12日に投稿する予定で、前の記事は元々今日投稿する予定でした。しかしバーニングシップ→燃えている船っていうのと8月12日という投稿日が日本航空123便墜落事故を連想させて嫌だったので公開順を入れ替えた、という経緯があります。
FNFE Projectは全部で35回の予定なのですが、個人的に「基礎」「標準・発展」「実践/戦」で構成をなんとなく分けていて、次回から「標準・発展」に入るという風に(勝手に)決めています。
なので次回から表現とかがちょっと難しくなり数学の知識もさらに必要になりますがそもそものテーマが難しいので許してください。
おまけ
本題には入らなかったけど面白い図形のギャラリーです。












