二状態マルコフ連鎖

メッセージを発する情報源は、一般的には、直前に発した記号に依存して状態を変え、その状態にしたがって次の記号を発信する、と考えることができます。ここでメッセージとは、情報源が一定のスピードで発する記号の列のこととします。

直前だけでなく、その前の、またその前の前の…というふうに、どれほど過去の履歴に依存するかは研究したいプロセスに依ります。ここではもっともシンプルなケース、すなわち直前の過去のみに依存した情報源を考えます。

数学的にはマルコフ連鎖とよばれるものです。具体的な設定は以下の図の通りです。

ここでα、βが情報源の内部状態を表し、矢印が遷移する向き、矢印についたラベルが遷移確率に対応しています。たとえばある時刻で状態αにいるときは、確率pで同じ状態に、確率p'で状態βに遷移することを表しています。

この図は行列のかたちで表すこともできます:

この表現の利点は、ある時刻で特定の状態にある確率が、この行列を用いて計算できる点にあります。最初の時刻に状態がαであったとすると、

のように次の時刻でそれぞれの状態にいる確率が求まります。さらに

のように２単位時間後に対しても同じ量が計算できます。一般にt単位時間後は

と計算できます。この行列を遷移確率行列といい、マルコフ連鎖を特徴づけます。もし行がまったく同じであると、遷移確率が状態に依存しないことになり、ベルヌーイ試行に一致します。

最初に情報源が状態αにいることが確定しておらず(すなわち状態ベクトルが(1,0)で表されず)、確率的にしかわからない一般的な場合を想定すれば、状態ベクトルは非負かつ１以下の実数rを用いて(r, r')と書けるでしょう。ここでr'=1-rです。

このような初期状態から出発して、t時間後に情報源がある状態にいる確率は、遷移確率行列の累乗の計算に帰着されることが上の結果からわかります。

そこで当然固有値と固有ベクトルを求めることになります。固有値方程式は

をゼロとおいたものとなり、これを解くと

の２つが固有値であることがわかります。このうち固有値１が重要です。というのも、１という固有値に対応する固有ベクトルは、確率の分布を変えない定常分布に対応するからです。これを計算するには、詳細釣り合いの式を立てればよい。いま、非常に多くのボールが、x:1-xの割合で、それぞれ状態αとβに割り振られているところを想像してください。一単位時間後には、状態αからp'xだけ状態βに移動し、逆に状態βからq'(1-x)だけ状態αに移動してくるでしょう。移動の前後でボールの割り振りが不変であるには、

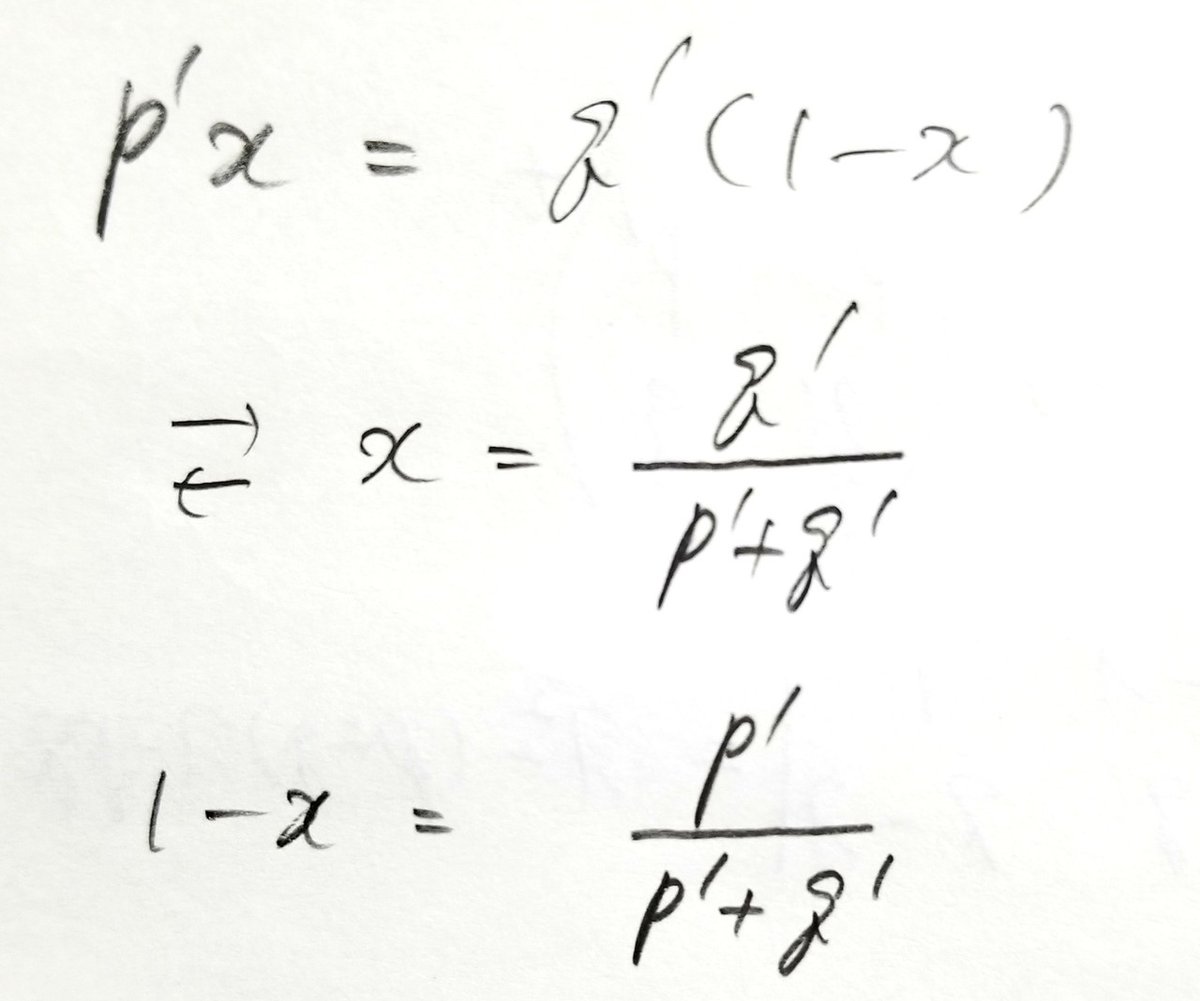
であればよいことがわかります。

残りの固有ベクトルは標準的な方法で求めることができ、(1,-1)となります。r-xをδとすれば、任意の状態(r, r')は、

と展開できます。これに遷移確率行列の累乗を右から作用させると、上式の右辺第二項は、対応する固有値p+q-1の絶対値が１より小さいことにより、時刻tが十分大きければ無視できるくらい小さくなります。(ここでp, qが同時にゼロもしくは１になる場合は省いています。)

つまり十分時間がたてば、情報源は最初の状態の記憶をなくし、共通の定常分布へと収束していくことになります。時間を無限に長くとった場合を想定すれば、情報源はほとんど確実にxの割合だけ状態αに、1-xの割合だけ状態βにいることになるでしょう。まだ最初の状態の余韻が十分強く残っている時間を過渡過程といいます。過渡過程の長さは「十分強く」の定義によりますが、いずれにしろたかだか有限です。それに比べ十分長い時間をとれるとすれば、上のような結論がいえることになります。

この結果をもとに、tが無限に大きくなる極限において、情報源が状態αにある確率P(α)が定義できます:

言葉でいうと、マルコフ連鎖で表現される情報源は、十分長いメッセージをとると、そこに含まれる記号の割合がある定常分布に近づく、ということになります。

次回はこの結果を使ってマルコフ連鎖におけるエントロピーの意味付けに迫りたいと思います。