
ハフマン符号化(瞬時復号可能性)
今回からハフマン符号化をみていきます。前回の議論はこちら:
瞬時復号可能性
事前準備として瞬時復号可能な符号を定義します。例えばa, b, cをある確率で独立に発する情報源があるとして、それぞれ1, 10, 100で符号化したとします。この符号は復号可能です。1が各符号の始まりを知らせているからです。ところが、符号列をリアルタイムで受け取って復号する側からすると、10を受け取った時点ではこれがbなのかcなのか瞬時に判断がつきません。次に0が来ればc、1が来ればbだったということになるので、待ちが発生します。大きな符号列を即時に復号することが求められる環境ではこれは大幅な時間ロスを生みます。
ところが0, 10, 11という符号はどうでしょう。この符号ならば待ちは発生しません。というのも、
どの符号をとっても、その先頭の一部が他の符号になっていることがないし、その符号が他の符号の先頭の一部になっていることもない
からです。0が来たらa、1が来たら待機、次に0ならb、1ならcというように、待ちが発生しません。このような符号を瞬時復号可能と定義します。
瞬時復号可能性と木構造
このような符号は木構造に埋め込むことができます。より正確には、木構造の終端に各符号を対応させることができます。たとえば先程の例では

のようになります。逆に木構造の終端を集めた符号は常に瞬時復号可能です。というのも、終端はその下の枝がないので、ある特定の終端に対応する符号が、別の符号の先頭に用いられている可能性はないからです。また同様に、ある終端の符号の先頭の一部が、他の符号になっていることもない。
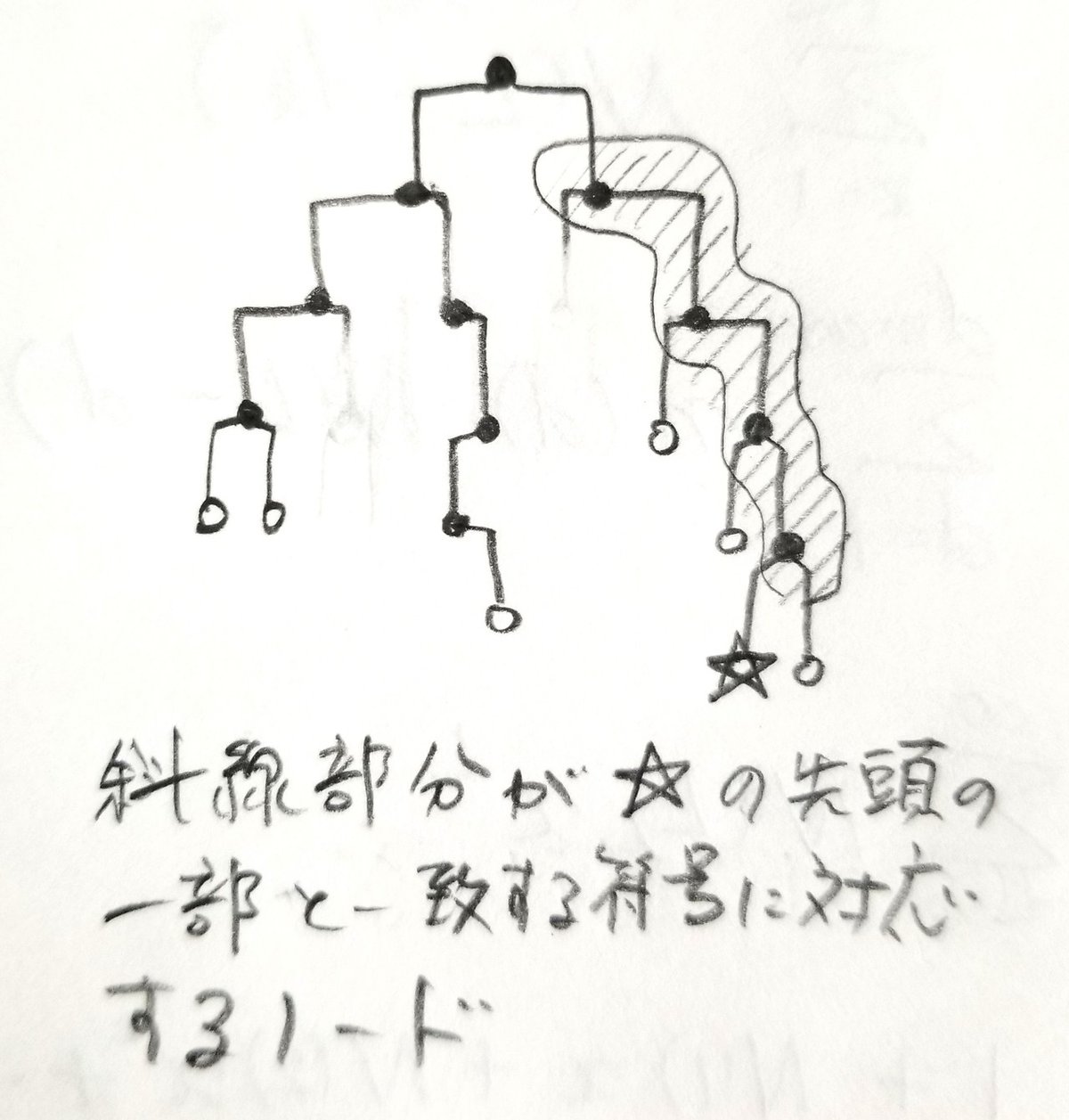
さて以上を踏まえて、以下の定理を証明します。
Kraftの定理
Kraft-McMillan不等式

がある符号長の組{dk}について成り立てば、同じ符号長の組を用いて瞬時復号可能な符号を構築することができる。逆に瞬時復号可能な符号は常にKraft-McMillan不等式を満たす。
まずは不等式から瞬時復号可能な符号が構築可能であることを示します。長さdの符号の個数をn(d)と置きます。するとこれは2^dを超えることはない。そうでないと不等式を満たさないからです。さてこのn(d)個の符号を、木構造の第d層に割り振ります。ここで木構造のあるノードの層とは、そこにたどり着くために必要な枝分かれの回数を指します。

割り振りが完了したあと、そこからたどり着ける下の層はすべてブロックします。こうしないと瞬時復号可能性が破られてしまうからです。残った2^d - n(d)個のノードは下の層で枝分かれして2倍のノードをつくります。このノード数とn(d+1)を比べると、n(d+1)の方が小さいか等しくなければなりません。さもないと

となって仮定に反する。つまり与えられた各dkを、dk層の終端に割り振ることができることが示されたわけです。さきほどの議論によってそのような符号は瞬時復号可能です。
次に逆を証明します。もしある符号が瞬時復号可能だとすると、それらの符号を木構造の終端に対応させることができるのは確認ずみです。そこで第d層にある終端に2^(-d)のエネルギーを割り当てましょう。どの枝分かれをとっても最終的にある終端にたどり着くような符号化の場合、全エネルギーの合計は当然1になります。(一枚目の図を参照。)しかし実際は使わない枝があってもいいわけですから(二枚目の図を参照)、全エネルギーは1以下となります。これで証明が完了しました。
ハフマン符号化
前回示した定理によって、ある符号が復号可能であれば、対応するdkの組がKraft-McMillan不等式を満たす必要があります。そして今回示した不等式により、同じdkで瞬時復号可能な符号が存在する。我々は{dk}をいろいろに動かして最適化をしたいわけですが、その探索範囲を瞬時復号可能な符号に限っていいわけです。なので以下では符号といえば瞬時復号可能な符号を指すとします。
さてある符号が最適であるとします。各記号をakとし、それが生起する確率をpkとします。ここで
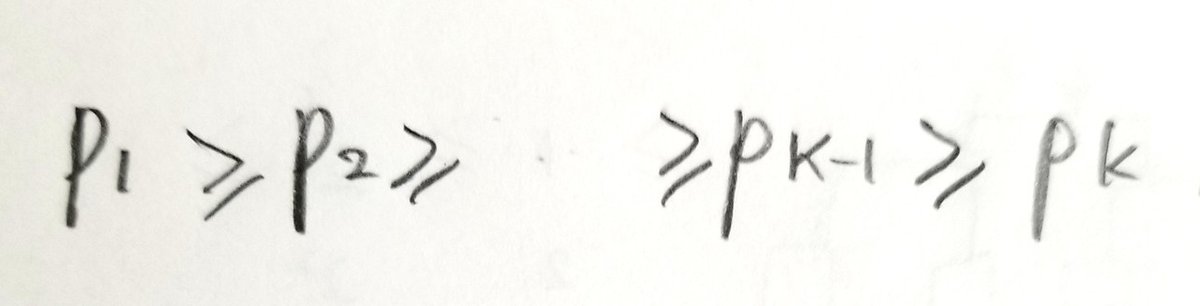
のように並び替えられているとします。akに対応する符号の長さをdkとします。
1. dk <= d(k+1)である。
これはもしそうでないとすると、dkとd(k+1)を交換することで、平均符号長をさらに小さくできるからです。よって特にdK=dmaxであることが分かります。
2. dKとd(K-1)は同じ長さである。
同じ長さでないとします。するとdK-d(K-1)の分の符号はdKから削除しても問題はない。というのもdKは最長の符号であり、瞬時復号可能な符号においてはどの符号をとってもその先頭の一部が他の符号であることはないからです。すると平均符号長をさらに小さくすることができ、符号が最適であることに矛盾します。
3. K番目の符号と同じ長さで、末尾のみ異なる符号が一つだけある。
まずK番目の符号以外で、dKの長さをもつ符号をすべて集めます。この中にはK-1番目の符号も入っている。次にK番目の符号とこれらの符号を比較して、K番目の符号と末尾以外が同じである符号が一つもないとすれば、K番目の符号の末尾は冗長になって削除できることになります。そこで少なくとも一つの符号はK番目の符号と末尾のみ異なる。また今は二値符号化を考えているので、このような符号はK番目の符号以外で最大でも一つしかないことになります。
4. 3.を満たす符号はK-1番目だと仮定できる。
もしK-1番目でないとしたら、K-1番目の符号と交換することで、平均符号長を不変に保つか、小さくすることができます。
5. K-1番目とK番目の記号を一つの記号で置き換え、その符号を元のK-1番目の符号とK番目の符号の共通部分とし、さらにその記号が確率p(K-1)+p(K)で生起すると仮定して定義される新しい情報源の平均符号長<d'>は、

を満たす。
これは4までの結果を使ってそのまま計算するだけなので詳細は省きます。
この関係式から元の情報源の符号の最適性は新しい情報源の符号の最適性に置き換えることができ、かつ新しい情報源は記号が一つ少なくなります。確率を大きさの順に並び替えて、再び同じプロセスで記号を減らしていけば、最後には記号が二つだけとなります。この場合明らかに最適な符号は0と1をそれぞれに割り振る場合達成されるので、今度はそこから逆向きに記号を増やしていけば、オリジナルの情報源の最適な符号が得られるというわけです。
実装例
ここでは疑似乱数を発生させて任意の記号数をもつ情報源のハフマン符号を構築します。pythonを学習中(学生時代はC言語でした)なのでpythonで実装してみました。以下の関数Huffmanはndarray型に格納された確率分布を入力すると、それらのハフマン符号と、情報源のエントロピー、平均符号長を算出して標準出力します。
import numpy as np
def Huffman(p):
dim = (p>0).sum()
step = dim
p = sorted(p, reverse=True)
nodes = []
code = []
entropy = -(p * np.log2(p)).sum()
codelength = 0
for index in range(dim):
nodes.append([p[index], set([index])])
code.append("")
while step > 1:
for index in range(dim):
if index in nodes[step-2][1]:
code[index] += "0"
if index in nodes[step-1][1]:
code[index] += "1"
nodes[step-2][0] += nodes[step-1][0]
nodes[step-2][1] = nodes[step-2][1] | nodes[step-1][1]
del nodes[-1]
nodes = sorted(nodes, reverse=True)
step -= 1
for index in range(dim):
codelength += len(code[index]) * p[index]
code[index] = code[index][::-1]
print(code)
print(entropy, codelength)この関数にたとえば
p = np.array([0.6, 0.2, 0.1, 0.05, 0.03, 0.02])を入力すると、出力として
["0", "10", "110", "1110", "11110", "11111"]
1.7194981241774019 1.75が得られます。二行目第一項の情報源のエントロピーよりわずかに二項目の平均符号長が大きいのが分かります。
次回はシャノンの符号化定理をKraft-McMillan不等式から導き、さらに瞬時復号可能な符号の平均符号長を上から評価していきたいと思います。
参考文献
[1] D.A.Huffman, "A Method for the Construction of Minimum-Redundancy Codes," Proceedings of the IRE 40, 1098 (1952).
[2] L.G.Kraft, "A Device for Quantizing, Grouping and Coding Amplitude-Modulated Pulses," M.S.Thesis, Dept. of Electrical Engineering, MIT, Cambridge (1949).
[3] B.McMillan, "Two Inequalities Implied by Unique Decipherability," IRE Transactions on Information Theory 2, 115 (1956).
[4] クロード・E.シャノン、ワレン・ウィーバー、『通信の数学的理論』、植松友彦訳、ちくま学芸文庫 (2009).
[5] R.G.Gallager, "Information Theory and Reliable Communication" (John Wiley & Sons, New York, 1968).
[6] 加藤公一、『機械学習のエッセンス』、SBクリエイティブ (2018).
