
Wiener, Gamma, and, Variance Gamma
"The conservatives are fools: They whine about the decay of traditional values, yet they enthusiastically support technological progress and economic growth. Apparently it never occurs to them that you can't make rapid, drastic changes in the technology and the economy of a society without causing rapid changes in all other aspects of the society as well, and that such rapid changes inevitably break down traditional values."
Generalized Hyperbolic (GH) 分布は、Variance Gamma (VG) を部分族として含む上位分布 (superclass)である。それなら、分布としてGHだけ使えばいいいじゃない?という疑問が生じるのは至極当然である。では、VGを使う理由とはなんなのか。
VG分布はVG過程から導ける確率分布であり、VG過程はWiener過程(Brownian motion)とGamma過程から構築することができる。即ち、Wiener過程に対してGamma過程によるランダムな時刻変更を行うことで、実時間における明示的なジャンプを再現している。そのため、市場で観察される不連続な値動き(Jump)をモデル化することが可能である。
即ち、VG過程X(t)はWiener過程W(t)とGamma過程G(t)を用いて
$${X(t)=\theta G(t)+\sigma W(G(t))}$$
と表せる。
Lévy Process
初期条件:X(0)=0
独立増分:任意の時刻区間$${[t_1,t_2],[t_2,t_3]}$$ $${0< t_1 < t_2 < t_3}$$に対してその増分$${X(t_2)-X(t_1)}$$と$${X(t_3)-X(t_2)}$$は互いに独立となる。
定常増分:増分の分布が時間に依存せず、区間の長さのみに依存する。即ち、任意のs,t>=0に対して、$${X(t+s)-X(s)}$$ $${X(t)-X(0)}$$の分布は一致する。
右連続・左極限性(càdlàg: continue à droite, limite à gauche):ほとんどの実現パスは、右連続であり、左側極限が存在する。これにより、不連続な変動が存在する場合も扱うことができる。
無限可分性 (Infinite divisibility):Levy過程が持つ増分の分布は無限可分可能である。これは、その増分がどのように小さな区間に分割されても、その分割された各部分の和が元の分布と同じ形になるという性質を意味する。
Wiener Process
初期条件:W(0)=0
独立増分:任意の時刻区間$${[t_1,t_2],[t_2,t_3]}$$ $${0< t_1 < t_2 < t_3}$$に対してその増分$${X(t_2)-X(t_1)}$$と$${X(t_3)-X(t_2)}$$は互いに独立となる。
定常増分:増分の分布が時間に依存せず、区間の長さのみに依存する。即ち、任意のs,t>=0に対して、$${W(t)-W(s) \sim Norm(0,t-s)}$$
連続性:W(t)はほとんど確実(almost surely)に連続である。
Gamma Process
初期条件:G(0)=0
独立増分:任意の時刻区間$${[t_1,t_2],[t_2,t_3]}$$ $${0< t_1 < t_2 < t_3}$$に対してその増分$${G(t_2)-G(t_1)}$$と$${G(t_3)-G(t_2)}$$は互いに独立となる。
定常増分:増分の分布が時間に依存せず、区間の長さのみに依存する。即ち、任意のs,t>=0に対して、$${G(t)-G(s) \sim Gamma(\frac{t-s}{\nu},\nu)}$$またこの時、期待値と分散はそれぞれ、$${E[G(t)-G(s)]=t-s, Var[G(t)-G(s)]=\nu(t-s)}$$
非負・単調増加性:G(t)はほぼ確実(almost surely)に非負であり、時間と共に単調増加する。
Variance Gamma Process
定義
まず、Wiener過程W(t)を用いてB(t)を以下のように定義する。
$${B(t)=\theta t+\sigma W(t)}$$
$${\thetaと\sigmaはそれぞれドリフトとボラティリティを表す。}$$
ここで、実時間tをランダムな時刻G(t)へ置き換える(subordination)ことでX(t)を構成する。
$${X(t)=B(G(t))=\theta G(t)+\sigma W(G(t))}$$
特性関数
どうして、X(t)がVG過程になるのか疑問に思う数弱くんのために、以下で示してあげよう。
X(t)がVariance Gamma分布に従うことを示すためにX(t)の特性関数を求める。
まず、Gmmma過程の値をG(t)=gを固定すると$${W(G(t))\sim N(0,g)}$$に従うため
$${X(t)|G(t)_{=g}=\theta g+\sigma W(g)}$$
これは、平均$${\theta g}$$、分散$${\sigma^2g}$$の正規分布$${N(\theta g,\sigma^2 g)}$$となる。
よって、条件付き特性関数は、
$${E[e^{iuX(t)}|G(t)_{=g}]=\exp[iu\theta g-\frac{1}{2}u^2\sigma^2g]}$$
ここで、正規分布の特性関数$${E[e^{itX}]=\exp[i\mu t-\frac{1}{2}t^2\sigma^2]}$$を用いた。
次に、Xの特性関数は全確率の法則より、
$${\phi_{X(t)}(u)=E[e^{iuX(t)}]=E_g[\exp(iu\theta g-\frac{1}{2}u^2\sigma^2g)]=E_g[\exp(g(iu\theta -\frac{1}{2}u^2\sigma^2))]}$$
一方で、Gamma分布のモーメント関数は、$${G(t)\sim \Gamma(t/\nu, \nu)}$$に従う時、
$${M_{G(t)}(z)=E[e^{tG(z)}]=(1-\nu z)^{-t/\nu},(\Re(z)<1/\nu)}$$
したがって、以下のようになる。
$${\phi_{X(t)}(u)=E[e^{iuX(t)}]=E_g[\exp(g(iu\theta -\frac{1}{2}u^2\sigma^2))]=(1-i\theta\nu u+\frac{1}{2}\sigma^2\nu u^2)^{-t/\nu}}$$
これは、Variance Gamma分布の特性関数と一致する。
以上よりX(t)はVariance Gamma分布に従うことが分かる。
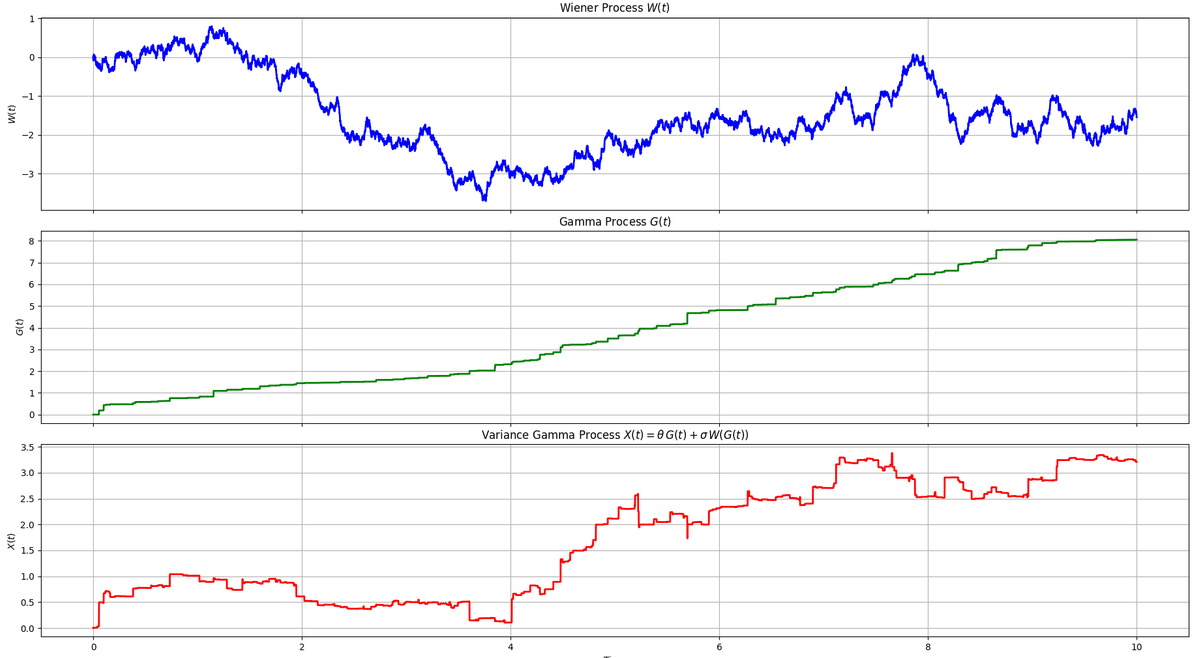
最後に、Wiener、Gamma、Variance Gamma過程をシミュレーションした。
図より、X(t)にはGamma過程のJumpが上手く反映されていることが分かる。
The Variance Gamma Process and Option Pricing
https://academic.oup.com/rof/article-abstract/2/1/79/1581894

