見出し画像

Normal Variance-Mean Mixture

gloomydog

When we stand together there is nothing, nothing, nothing we cannot accomplish.

Bernie Sanders

Normal Variance-Mean Mixture

Normal Variance-Mean Mixture (NVMM)とは混合変数 S を用いて、確率変数 X を次のように表現するモデルである。

  • $${\mu}$$は位置パラメータ

  • $${\theta_0}$$はシフトパラメータ

  • Tは標準正規分布に従う独立な乱数

  • Sは(0,∞)上の非負混合変数

  • $${\theta_0=0}$$のときはnomal variance mixtureという。

このモデルでは、条件付きS=sとしたとき、Xの条件付き分布が以下のようになる。

Sの確率密度関数を$${f_S(s)}$$とすると、Xの全体の確率密度（Xの周辺確率）は、「全確率の法則」を用いて

と表せる。ここで、条件付き確率$${f_{X|S}(x|s)}$$は

混合変数Sの分布に応じて、Xの分布がいかなる形状（裾の厚さ(fat-tail)、ゆがみ）を持つかを決定する。

Brandorff-Nielsenなどの研究により、GH(generalized hyperbolic)分布の多くは、このNVMMで表現が可能とされている。

GHの派生分布

以下では、モンテカルロ法でXのhistogramを作り、解析解(Closed-form expression) $${f_X(x)}$$と比較し、実際にGHの派生分布がNVMMで表現できているか実証した。

Variance Gamma

VGはGHの上位互換(Superclass)に該当する。
Sがガンマ分布に従う時、XはVGとなる。

VGのNVMM
Closed form of Variance Gamma
mu=5, theta_0=2, sigma_0=4, a=3

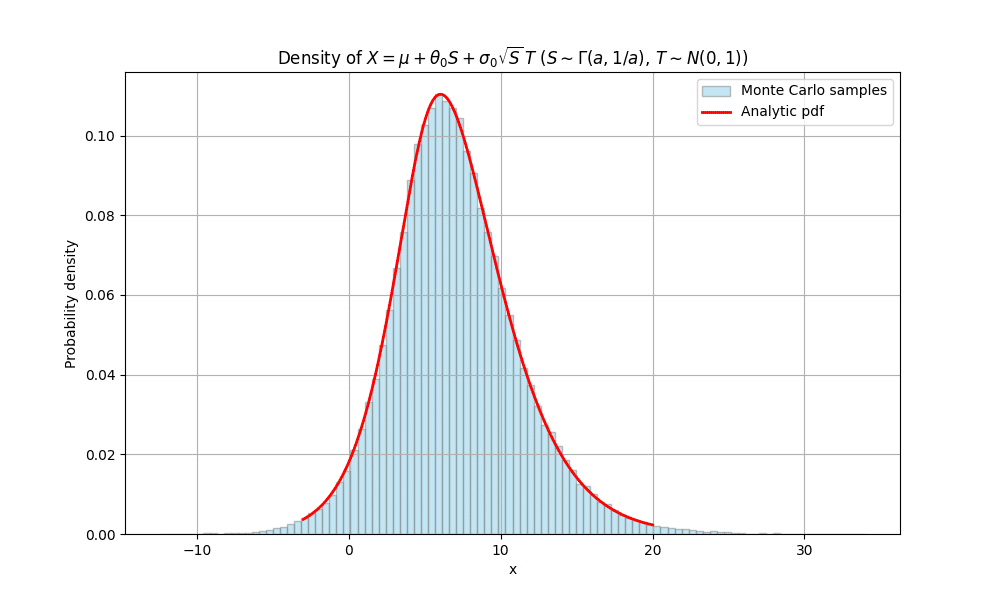
GH: Generalized hyperbolic

SがGIG(Generalized Inverse Gaussian) に従う時、XはGHとなる。

Closed form of Generalized Hyperbolic

NIG：Normal-inverse Gaussian

$${\lambda=-1/2}$$のときGIGはIG(Inverse Gaussian)の分布と一致し、SがIGに従う時、XはNIGとなる。$${\gamma=\sqrt{\alpha^2-\beta^2}}$$

Closed form of NIG

Skewed Student's-t

Sが逆ガンマ分布に従う時、Xは歪曲Student's-t 分布となる。

Closed form of skewed student's-t
mu=3, theta_0=3, sigma=3, alpha=beta=6

Student's-t

Sが逆ガンマ関数に従い、$${\theta_0=0}$$かつ$${\alpha=\beta=\nu/2}$$の時、XはStudent's-tとなる。

Closed form of X with $${\alpha}$$and$${ \beta}$$
Closed form of Student's-t
mu=3, theta_0=0, sigma_0=3, alpha=beta=6

Asymmetric Laplace

Sが指数分布に従う時、XはAsymmetric Laplaceとなる。

Closed form of Asymmetric Laplace
mu=3, theta_0=2, sigma_0=3, lambda=4

Laplace

Sが指数分布に従い、$${\theta_0=0}$$ かつ　$${\lambda=1}$$のとき、XはLaplaceとなる。

Closed form of Laplace
mu=3, theta_0=0, sigma_0=3, lambda=1


いいなと思ったら応援しよう！