
【盲点!】相関が[無い]なら、因果が[無い]。この命題は真か偽か?
お疲れ様です。東京で仕事をしているものです。へちやぼらけと申します。(統計学・機械学習に関する動画も投稿してます。YouTuberです。笑)
筆者の最近の興味事は「因果推論」。皆さんにも因果推論の魅力を知って欲しい!ということで、因果推論を解説する動画を投稿してみました!
〇「相関・因果・交絡因子」
今回は「因果推論」に関する記事です。突然ですが、「相関関係がある(強い)からと言って、因果関係があるとは限らない」という事実をご存知でしょうか・・・?
残念なことに「相関が強い=因果関係がある!」と誤認している方が多い。確かに、ややこしい。相関が強い場合には「片方のデータが増えるほど、もう片方のデータが増加(or減少)する」んだから、2つのデータに因果関係あっても良くない?と思っちゃいますよね。
でも、実際は違う。何故、こんなことが起きるのでしょうか?それは『交絡因子』と呼ばれる第3の変数よって引き起こされます。この交絡因子が2つの変数に影響を与えている性で、因果関係が無いにも関わらず見かけ上相関が出てくるんです。

例を挙げれば一発で理解できます。例えば、血圧(X)と年収(Y)のデータ。2つのデータを点プロットしてみると綺麗な正の相関関係を持ちます。
ただ、血圧(X)と年収(Y)に因果関係があると言えるでしょうか?普通に考えてそんなはずはないですよね。この現象は、年齢(Z)という交絡因子が存在していて、それが血圧(X)と年収(Y)の両方の原因となっているために起こります。
年齢が上がると血圧が上がる・年齢が上がると年収が上がる。よって、血圧と年収に見かけ上の相関が現れてくるんです。こういった見かけ上の相関を『擬似相関』と呼んだりもします。

この辺の話について極めて平易に解説されている記事があったので、ご連携します↓↓
〇やっと本題!
本題です。記事のタイトルを回収します。
さて。「相関関係があるからと言って、因果関係があるとは限らない」について理解できました。ただ、ここでもう1つステップアップ。この命題の逆に着目します。つまり「相関関係が無いからと言って、因果関係が無いとは限らない」。この命題は果たして真か偽か?
この事実に関しては、意識している人って少ないですよね。相関があった時には「交絡因子」を頑張って探して、「因果関係は無い!」と主張する。でも、相関が無かった時はどうでしょう?無条件で因果無しって断定してません?今回の記事では、この件について深堀していくぜ!
①直線じゃない因果関係
まずは、2つのデータの散布図が直線じゃない場合。相関係数はあくまで2つのデータの増減関係を-1~+1で表す指標なので、散布図が「ドーナツ型」だったり「二次曲線の場合」は明らかに因果関係がありますが、相関は0に近くなります。

ドーナツ型の場合を因果推論のフレームワークである「構造方程式」「構造モデル」で表すと下の様な感じ。
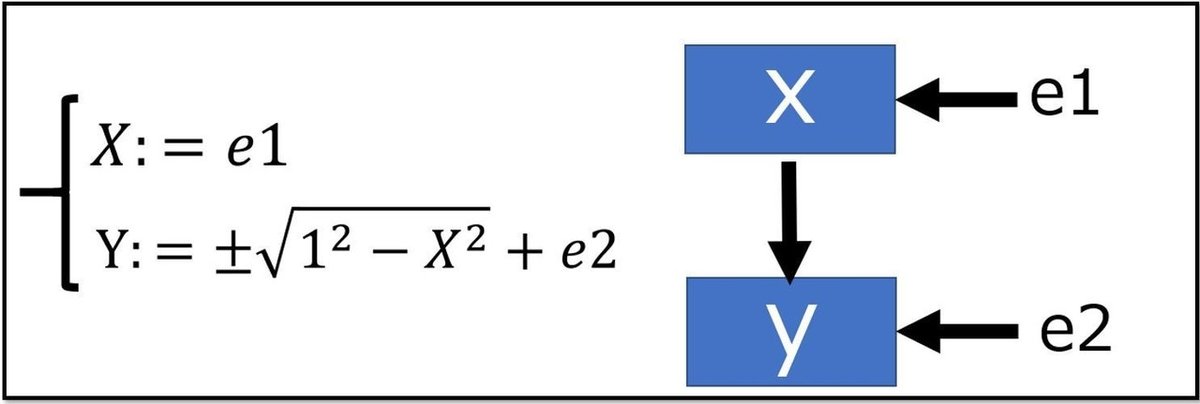
二次曲線の場合を因果推論のフレームワークである「構造方程式」「構造モデル」で表すと下の様な感じ。

①のケースの話はこれでお終い。この場合は、散布図を見れば「相関0でも因果関係ある」なっていうのは明らかにわかりますね。
②原因と交絡因子が逆に作用する
2つの変数X,Yは「原因」「結果」の関係になっているが、交絡因子により各々逆の力が働くケース。下の様なイメージを持っていただければ良いです!

直観的に言えば、起こり得そうな気がします。どうですか?起こりそうじゃないですか?
考えれば考えるほど気になってくるため、数学的に確認しようと思います。構造方程式・構造モデルを使っていきます。
構造方程式と呼ばれる因果推論を記述するフレームワークを使えば、上記の疑問はすぐに解決できるはず。(ちなみに、構造方程式と言いつつも、実態は単純な方程式だったりもするので、以降は深く考えずに式を追ってみて下さい。)

「交絡因子により各々逆の力が働く」というのは、上の図で言えば、Xには+2倍しているのに対して、Yには-2倍しているということ。Zが1単位増えれば、Xに+2単位の影響を与える。その一方で、Yにー2単位の影響を与えている。また、XはYの原因となっており、Xが1単位増えれば、Yも1単位増えます。
あと、誤差項e1,e2,e3を与えておりますが、特に複雑に考えず、それぞれ独立の標準正規分布に従うと仮定しましょう。
これを数式で表したのは、上の図の左の3元1次方程式。
さて、この方程式を整理してみます。すると・・・。


ということで、共通項e1が残りましたね!
共通項が残るということは、「XとYは独立ではない!」。すなわち、「共分散が0ではない!」。すなわち、「XとYには相関がある」と言えますね。これ以外にも、係数を一般化したりして検証してみましたが、どうあがいても共通項e1を消すことができませんでした。
なので、結論としては『因果関係があるにも関わらず、交絡因子の影響で見かけ上相関がなくなる。なんてことは、あり得ない』。ということを数式から証明できました。
この記事が気に入ったらサポートをしてみませんか?
