【XAI・説明可能なAI】SHAPも多重共線性には勝てない?という話【実例あり】

こんにちは。横浜在住のデータサイエンティスト、へちやぼらけです。

名著『機械学習を解釈する技術』を読みました。近年、注目を浴びている「機械学習の説明可能性（XAI）」について解説をされている本です。

機械学習を解釈する技術、本日8/4から発売されます！PFI, PD, ICE, SHAPの4つの機械学習の解釈手法を、ライブラリを使わずPythonでゼロから手法を実装することを通じてアルゴリズムを理解し、データ分析を通じて勘所を掴んで頂けるよう工夫しました！https://t.co/3ofl7zopti

— 森下光之助 (@dropout009) August 4, 2021

　この本のタイトルにもなっている「機械学習を解釈する技術」とは、端的に説明すると『どの説明変数がどれくらい予測結果に寄与（影響）しているのか計算する手法』のことです。構築した機械学習モデルを実業務で利用し始めると、上司やら経営層から「AIがどうしてこんな予測結果を示したんだ!!? 説明しろ!!」と詰められることは良くあることだと認識しておりまして、頭を悩まされているデータサイエンティストの方も多くいると思われます。「機械学習を解釈する技術」を使えば、各説明変数に対して予測値への寄与度が数値化されるため、AIがどうしてそんな予測結果を出したのか簡単に説明できるので大変便利です。

　ちなみに、機械学習を解釈する技術と一口に言っても様々な手法があるのですが、この本では ”PFI”, "PD", "ICE", そして、"SHAP(SHapley Additive exPlanations )"について解説をされています。さて、この本で紹介いただいた4つの手法のうち、実務で圧倒的に使われるのはSHAP(SHapley Additive exPlanations )ではないでしょうか？
※SHAPについて詳細を知りたい方は、下記リンク参照。

SHAP(SHapley Additive exPlanations)で機械学習モデルを解釈する - Dropout

　名著『機械学習を解釈する技術』では、数値シュミレーション・実データを用いた解説があって非常に分かり易かった。

　重回帰分析をする際、説明変数同士で高い相関があった場合（即ち、多重共線性があった場合）、回帰係数の値が大きくぶれるので「各変数の回帰係数の値＝予測への影響度」と解釈するのは危険だぞ～、と口を酸っぱくして言われたものです。これと似たような話が”PFI”, "PD", "ICE"でも同じ様なことが言えるらしく、「説明変数同士に強い相関があった場合、それら説明変数同士が互いに影響度を喰いあう形となり、個々の重要度が減少する」らしいです。同著では、これを実シュミレーションを使って解説されており、大変分かり易かった。

　ただ、残念なことにSHAPについては、そのシュミレーションがありません。ですので、この記事ではSHAPを対象に「目的変数同士で強い相関を持つ場合（回帰分析的に言えば、変数同士で多重共線性がある場合）変数の影響度がどうなるのか？実例を用いて解説いたします。

①【始めに】前提の確認

　検証結果について報告する前に、まず、今回の検証の対象となる学習データについて軽くお話させて下さい。今回はBoston Housingデータと呼ばれるデータサイエンス界隈で有名なデータを用います。以下、Boston Housingデータの概要の説明です。

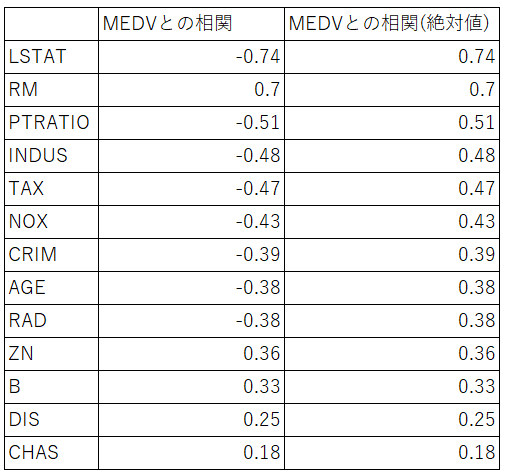
　一応、目的変数・説明変数のデータの相関を確認してみました。下の表は目的変数MEDVとの相関の絶対値が大きい順に並べたものです。相関係数の絶対値が大きい順にLSTAT ＞ RM ＞ ＞CRIME ・・・＞ CHASとなっています。

　下の図に２種類の図があると思いますが、左側の図は『目的変数(MEDV)とLSTATの散布図』となります。右側の図は比較用として、相関係数の低かったCRIMEの散布図を載せています。

　では、Boston Housingデータを使って、実際にモデルを構築し、目的変数の予測に寄与する変数は何か？確認していきましょう。

　以下の表が予測に寄与する変数順に並べた表です。以下の表からわかる通り、MEDVを予測する際に大きな影響を与えているのが、大きい順に LSTAT, RM, DIS・・・だということがわかります。

　ちなみに、SHAPの影響度と相関係数の絶対値の大きさを見比べてみると、ほぼ同じ結果になっています。目的変数と相関が高いなら、予測に寄与する変数として上位に登場するかー、と納得しつつも、だったらSHAPを使わなくても、単純に目的変数の相関をとってあげればそれで良くね？と思ったりしました。。

　以下のグラフは、学習データ・XGBoostのパラメタ(random_state)を乱数を用いて少し変えながら、1000回シュミレーションを回し、それぞれのシュミレーションで得られたLSTATのSHAP値をヒストグラムにまとめたものです。

②説明変数同士で強い相関を持つ場合

　さて、やっとここで本題。説明変数同士で強い相関を持っていた場合、予測への影響度はどうなってしまうのか？確認していきます。今回の実験では、LSTATと強い相関を持つ説明変数（LSTAT_COPYと命名・LSTATとの相関は0.99）を疑似乱数を用いて作り出し、その変数を学習用データに加え、XGBoostでモデルを作り、SHAPを求め、SHAPの値がどうなるのかを確認していきます。

　下記の表がその結果です。学習用データにLSTAT_COPYを含まない場合・含む場合のLSTATの影響度をそれぞれ載せています。下の図を見てわかる通り、説明変数同士で強い相関があると、予測への影響度が小さなってしまうことを確認できます。

　①と同様に②でも1000回シュミレーションし、影響度をヒストグラムにまとめました。左側の濃い赤のヒストグラムがそれです。また、右側にうっすらピンク色のヒストグラムがあると思いますが、これは①でお見せしたLSTAT_COPYを含まない場合のヒストグラムです。

ちなみに下の図が、LSTAT_COPYのSHAP値をヒストグラム化したものです。

　LSTATとLSTAT_COPYのSHAP値の和をとったものが下の図の灰色のヒストグラムになります。薄いピンク色のヒストグラム（①でお見せした LSTATのSHAP値のヒストグラム）と比較してみると、ほぼ一致することがわかります。つまり、LSTAT_COPYが説明変数として追加されたことで、LSTATの影響度は減少したが、それは相関の強いLSTAT_COPYとSHAP値を喰いあうことによるものであると推測が立ちます。

③【補足】相関係数をもう少し緩めてみると‥。

　②の例では、LSTATとLSTAT_COPYの相関は0.99であり、データ上、ほぼLSTAT＝LSTAT_COPYです。少し、両者の相関を緩めて、同じ様にSHAP値のヒストグラムを描いてみるとどうなるのでしょうか？確認していきましょう。

　下の図は、LSTATとLSTAT_COPYの相関が0.93の場合のSHAP値のヒストグラムです。驚いたことに、疑似的に作成した変数LSTAT_COPYの予測への影響度が殆ど0になっていることが確認でき、LSTATの予測への影響度は、LSTAT_COPYを追加する前のソレと殆ど同じなっていることが確認できます。

　疑似的に作ったLSTAT_COPYの影響度が0に近い値をとるのは、感覚的には良い気がするのですが、とは言え、LSTATと相関の強い変数ですし、目的変数との相関が「-0.69」で負の相関はそこそこあるんですけどね。いまいち納得行くんだか、行かないんだか良くわからない結果となってしまいました。色々調べていくと、沼にハマっていきそうなので、今回の記事はこの辺で終わりたいと思います。皆さんはどのように思われますか？？