
階層クラスタリングやDBSCAN
前回の続きです。
今回のテーマはデンドログラム(樹形図)による階層クラスタリングをまず取り扱います。
非常に直感的理解がしやすいデンドログラムでk-meansのようなクラスタの数をこちらで決める必要もありません。
階層クラスタリングには凝集型と分割型があり、
凝集型は全てのデータ点が一つのクラスタに収まるまでクラスタをマージしていき、
分割型はその反対で最初のデータセットを一つのクラスタと見なし、クラスタ内にデータがひとつしか残らない状態になるまで分割を繰り返すことを意味します。
では、行ってみましょう。
・簡単な理論背景〜グループ化の方法〜
凝集型においてどのデータをくっつけていくかを判断する時に、距離の測り方(決め方)がたっっくさんあります。
ここでは代表的なものを簡単に紹介してから、その後にパラメータなどでそれぞれの違いなどをみていけるとスムーズかなと思います。
そもそも(凝集型)階層的クラスタリングのアイデアとしては以下。
1. 全ての点をそれぞれクラスタとして考える(n個のデータであれば、n個のクラスタがあるとしてスタート)
2-1. 全てのクラスタのペアを考えて、距離を測定
2-2. 採用した距離の測り方に基づき一番小さいペアを合体
3. 2-1, 2-2を目標のクラスタになるまで繰り返し
では、測り方の指標をみていきます。
1. 単連結法(最短距離法)
クラスタ同士で最も近いデータ点の距離を測り、一番近い距離のペアをマージする考え方
2. 完全連結(最長距離法)
単連結の反対で、クラスタ同士で最も離れているデータ点の距離を比較して、一番小さいクラスタをマージしていく方法。
簡単に図示すると以下。

(若干の厳密性を欠いている気がしなくもない。。。)
3. 重心法
クラスタ内の重心を計算して重心同士が近いクラスタをマージする
4. Ward法
SSE(クラスタ内の誤差平方和)の合計を計算し、クラスタ同士のSSEを足し合わせて、最も増加する量が小さいクラスタ同士を比較する方法
5. 平均連結法
クラスタ同士で各データ点における最小距離を求めてその平均が一番近いクラスタ同士をマージする
1~5までサラッと書きましたが、一番分類感度が高いのがWard法である(ただし計算コストが高いこと)、外れ値に強いのは重心法(分類の感度はWard法)である、くらいの認識でまずはおけです。
・データの準備
上記の距離の測り方などを確認していくために少しデータを準備します。
import numpy as np
import pandas as pd
np.random.seed(123)
variables = ['X', 'Y', 'Z']
labels = ['ID_0', 'ID_1', 'ID_2', 'ID_3', 'ID_4']
# shape = (5, 3)かつそれぞれのデータが0~10の範囲の値を取る
data = np.random.random_sample([5, 3])*10
df = pd.DataFrame(data, index=labels, columns=variables)
df
特に説明することもないので、次にいきます。
・実際に距離を測り、階層クラスタリングをしてみる
今回は距離行列なるものを使いますが、後ほど使うlinkageは距離行列でなくてもいろんなアプローチがあります。
とりあえず距離行列をコードでみていきます。
from scipy.spatial.distance import pdist, squareform
row_dist = pd.DataFrame(squareform(pdist(df, metric='euclidean')))
row_dist
(私も含めて)なんじゃいなこれって方に向けて、pdistとsquareformを捕捉します。
ドキュメントはこちら。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.pdist.html
とはいえ、簡単にいえば、全ての行に対して指定した計測方法(今回であればユークリッド距離(L2norm))でそれぞれの行との距離を測り、それを順番に配列に格納していきます。
ちょっと自作で関数を作るとそれぞれの行に対して以下の処理が行われているイメージ
def dist(index1, index2):
arr1 = df.loc[index1, :]
arr2 = df.loc[index2, :]
arr = arr1 - arr2
return np.linalg.norm(arr)
dist('ID_0', 'ID_1')
最初のID_0とID_1の数値と合致しましたね!
squareformに関してはこの配列を対象に配置したものを生成します。
公式ドキュメント
https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.squareform.html
(どちらかと言えばpdistを使ったのち、どうにか行列にしたいときに使う感じで、ここではそこまで深掘りせずにいきます。ちなみに、row_distも以下で使いませんww)
・linkage、dendrogramで可視化していく!
今回のテーマの中で一つの重要なポイントです。
先ほどまで距離行列でそれぞれの点の距離を測りました。これらを用いて回想的にクラスタリングしてきます。
まずはlinkageから。
先に公式ドキュメントから入ります。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.hierarchy.linkage.html
scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean', optimal_ordering=False)
y: ndarrayの形式!各クラスタの距離が格納された配列を指定(pdistなど)
method: 先程の最短距離法やWard法を指定(結構たくさんありますが、最初はWardとかを指定するのが無難ぽい)
’single’: 最短距離法
'complete': 最長距離法
'average': 平均連結法
'centroid': 重心法
'ward': ward法
metric: 距離の計算方法。ミンコフスキー距離やコサイン距離などが他にある。
optimal_ordering: 出力されるlinkage matrixにおいてdistanceの要素を照準にするかどうか。Trueにすると非常に計算コストが高くなるため、非推奨
linkage関数の返り値はn次元の配列で格納されます。
では、実際にコードをみていきましょう。
# 最長距離法
row_clusters = linkage(pdist(df), method='complete')
# row_clustersの中身を見やすくするために簡易的にDataFrameにして表現。
pd.DataFrame(row_clusters,
columns=['row label 1', 'row label 2', 'distance', 'no. of items in clust ..'],
index = [f'cluster {i + 1}' for i in range(row_clusters.shape[0])])
これをパッと見ても(私は)ピンとこないので、デンドログラムを先に用いて可視化してから戻ろうと思います。
from scipy.cluster.hierarchy import dendrogram
dendrogram(row_clusters, labels=labels)
plt.ylabel('Euclidean distance')
plt.tight_layout()
plt.show()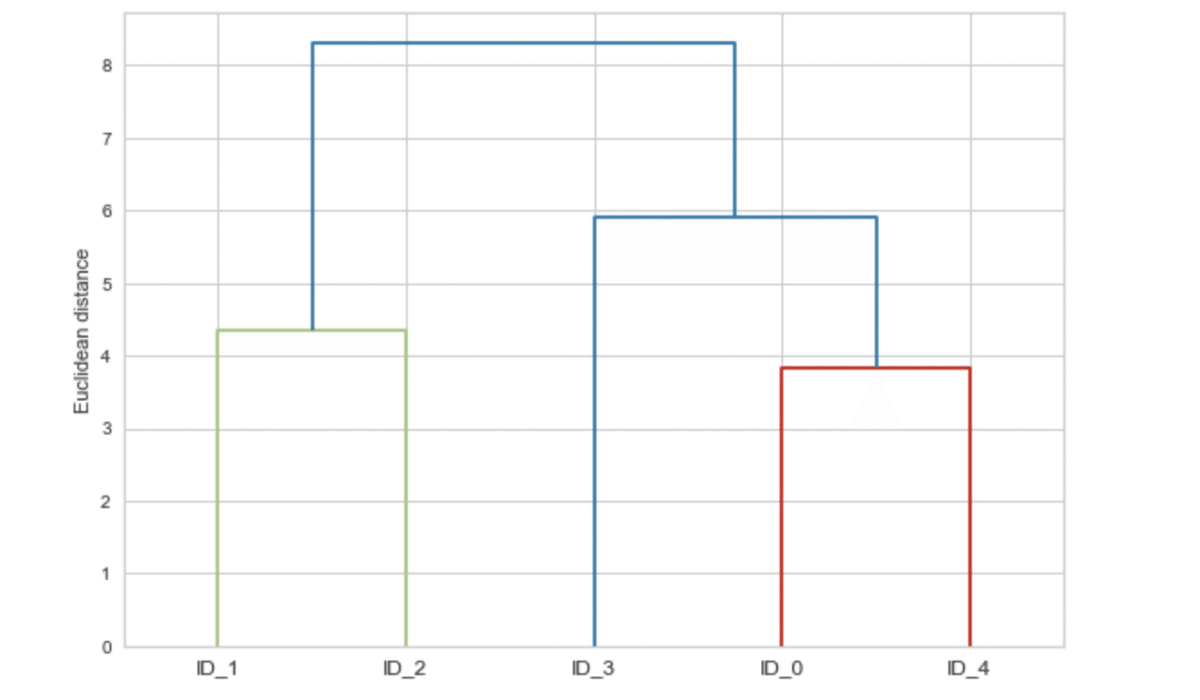
順番に行きますね。。
まず、

cluster1では最長距離で各クラスタ(最初なので全てのデータ点がクラスタとして扱われている)の距離で一番近いものをマージします。
今回で言えば、ID_0とID_4(というクラスタ)が近いため、マージされてcluster1 というクラスタが生成されました。
次にcluster1, ID_1 ~ID3というクラスタの中の距離で一番近いもの(cluster1 とID_~を比較する場合は距離が遠い法を代表として採用)は、ID_1とID_2の距離が一番近いためこれをマージしてcluster 2として採用します。
そして、cluster1, cluste2, ID_3に同じように距離を比較して最終的に全てのデータ点が1つのクラスタ(今回の場合cluster4のこと)になるまで繰り返します。
これを可視化して表したものがdedrogramとなります。
今回このdendrogramに関しては可視化ツールとしてみるため、がっつりとした詳細は本筋から逸れるため割愛します。
気になる方は公式ドキュメントを
https://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.hierarchy.dendrogram.html
これらのパラメータをいじることでより華やかな描画にできます
・dedrogram をヒートマップと組み合わせる
このdedrogramはヒートマップと組合してみることも多い(らしい)ので、その方法を見ていきます。
----ちょっとコメント-----
可視化というものはいくらでも繊細に扱うことができますが、いちいち覚えてられないくらいたくさんありますので、あまり深追いせず、最初は「ふ〜ん」くらいで流し見(写経)とかで十分です。(自分も覚えてませんし。。)
---------
ざっとコードと結果を見てから、補足していきます。
fig = plt.figure(figsize=(8, 8), facecolor='white')
# 軸の設定
# x軸の位置, y軸の位置 , 幅, 高さ
axd = fig.add_axes([0.09, 0.1, 0.2, 0.6])
row_dendr = dendrogram(row_clusters, orientation='left')
# dendrogramの返り値はdict形式。
df_rowclust = df.iloc[row_dendr['leaves']][::-1]
# ヒートマップの配置設定
axm = fig.add_axes([0.23, 0.1, 0.6, 0.6])
# ヒートマップを格納
cax = axm.matshow(df_rowclust, interpolation='nearest', cmap='hot_r')
axd.set_xticks([])
axd.set_yticks([])
for i in axd.spines.values():
i.set_visible(False)
fig.colorbar(cax)
axm.set_xticklabels([''] + list(df_rowclust.columns))
axm.set_yticklabels([''] + list(df_rowclust.index))
plt.show()
見慣れないmatplotlibのメソッドがたくさんあって「うぇぇ。。」って(私は)なりますが、あまり気にせず、ポイントポイントのみ解説します。
- 最後の方のaxes.spinesに関して
グラフの軸に関する表示の有無などを決める場合に使います。
ちなみに、今回軸がなんか表示されちゃってるんですが(原因不明。。)、本質ではないので、飛ばします。。
・sklearnでさっくりと凝集型階層クラスタリングを適用する
先ほどまでの内容を(当然ながら)sklearnが実装しているので、見ていきます。
from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='complete')
labels = ac.fit_predict(X)
print(f'Cluster labels: {labels}')
では、公式ドキュメントより
class sklearn.cluster.AgglomerativeClustering(n_clusters=2, *, affinity='euclidean', memory=None, connectivity=None, compute_full_tree='auto', linkage='ward', distance_threshold=None, compute_distances=False)
n_clusters: 先程の凝集型と違い、k-means ライクな欲しいクラスタだけ取得することができます。
affinity: linkageのmetric(類似度の指標)を指定するイメージ。linkageで'ward' を指定している場合以外は、'l1', 'l2', 'cosine'などが指定可能('ward'のときは'euclidean'のみ)
memory: 使うCPUの数
connectivity: 隣接行列の設定(隣接行列を知らないのですが、こちらのサイトが外観がわかりやすかったです。)今回のdendrogramのようなアルゴリズムでは基本的に構築されない(らしい。)
compute_full_tree: クラスタの数がサンプルに比べ非常に大きい時に計算コスト削減に役立つもの(基本的にconnectivity matrixが設定されている時利用可能)
linkage: 類似度の精度指標を設定('ward', 'complete'などなど)
distance_threshold: linkageの類似度計算時に閾値を設定してそれ以下でないとクラスタの生成をしないようにする
compute_distances: クラスタ間の距離を計算するかどうか
ざっとこんな感じですが、今回この中のfit_predictメソッドを用いることで、訓練したXの各データ(行数の数だけ)がどのクラスタに属しているのかというラベルをリスト形式で返してくれます。
少しだけパラメータを変えてみると以下。
ac = AgglomerativeClustering(n_clusters=2, linkage='ward')
labels = ac.fit_predict(X)
print(f'Cluster labels: {labels}')
ac = AgglomerativeClustering(n_clusters=2, linkage='complete')
labels = ac.fit_predict(X)
print(f'Cluster labels: {labels}')
wardとcompleteではクラスタの形成のされ方が違う結果となりました。
先程のようにわざわざ可視化などせずラベルの結果だけ欲しいという場合はサクッとこちらでいいのかもしれませんね。。
・DBSCAN
・DBSCANとは?
今回の最後のテーマであるDBSCANを紹介して終わりにしましょう。
DBSCAN(density-based Spatial Clustring of Applications with Noise)の略ですが、普通に「DBSCAN」でw
これまでのクラスタリングと違い、球状にクラスタが広がっていなくても、階層的な分割も行わずに、着目するのは「データの密集度合い(density)」です。
のちに扱いますが、波状に広がるようなデータセットにおいて有効的です。
デメリットも後ほど紹介しますが、まずは理論から。(いつもながら、とにかく使ってみたいという方は流し見で大丈夫です。)
・DBSCANの簡単な理論背景
文章で説明するのも非常にわかりにくく、また参考テキストもいまいちな図だったので、自分で作りながらすこし丁寧に見ていきましょう。
とはいえ、まずは文章ベースで。
1. 半径εとその半径以内に何個最低限データがあって欲しいのか?というMinPtsという数値を自分で決めます(ハイパーパラメータ)
2. 1.にて半径εにMinPts以上データ点を持つデータ点をコア点とみなす
3. ε以内にMinPts個のデータ点は持たないものの、2. で決まったコア点から見て半径ε以内に存在する点をボーダー点とします。
4. その他の点全てをノイズ点とみなします。
では、図で見ていきます。

今見ていくデータ点は上記のように散らばっているとします。(MinPts=3としておく)
次にεを決めて、ひとつひとつMinPts個以上の点を含んでいるかどうかを確認していきます。

例えば、上記の水色の点はコア点と見なすことができます。

上記の示した点に関してはMinPts個に満たすデータ点を確保できないため、スルーします。
これを全てのデータ点で見ていきます。

最終的には上記のようになります。
すこしあえてボーダー点が被るようにな配置になりましたが、基本的には配置が決まれば、
コア点の接続関係に基づき別々のクラスタを形成する(上記の場合はコア店同士が同じクラスタとカウント(状況による))
これによりノイズ点による外れ値の影響なども受けにくく、kmeansや階層クラスタリングとは一線を画していますね。
・pythonでDBSCANを実装
今回はkmeansや階層クラスタリングではクラスタリングできないような状況でDBSCANの威力を見ていきます。
データの準備からしていきますが、詳細な説明などは割愛します。
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
plt.scatter(X[:, 0], X[:, 1])
plt.tight_layout()
plt.show()
まずは復習がてら、kmeansでk=2ではどのように区切られているのか見ていきましょう。
kmeans = KMeans(n_clusters=2, n_init=10)
y_km = kmeans.fit_predict(X)
plt.scatter(X[y_km==0, 0], X[y_km==0, 1], color='green', marker='*')
plt.scatter(X[y_km==1, 0], X[y_km==1, 1], color='blue', marker='s')
plt.title('KMeans: k=2')
plt.tight_layout()
plt.show()
やはり球状に分割しようとしているため、うまくクラスタを認識できていないことがわかります。
次に、階層クラスタリングのsklearnのAgglomerativeClusteringでもどういうクラスタリングになるか見ていきます。
ac = AgglomerativeClustering(n_clusters=2, linkage='ward')
y_ac = ac.fit_predict(X)
plt.scatter(X[y_ac==0, 0], X[y_ac==0, 1], color='green', marker='*')
plt.scatter(X[y_ac==1, 0], X[y_ac==1, 1], color='blue', marker='s')
plt.title('Agglomerative Clustering: k=2')
plt.tight_layout()
plt.show()
階層クラスタリングもやはりうまくクラスタリングできていません。
では、本題のDBSCANで見ていきましょう。
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.2, min_samples=5, metric='euclidean')
y_db = db.fit_predict(X)
plt.scatter(X[y_db==0, 0], X[y_db==0, 1], color='green', marker='*')
plt.scatter(X[y_db==1, 0], X[y_db==1, 1], color='blue', marker='s')
plt.title('DBSCAN')
plt.tight_layout()
plt.show()
お見事!っていう感じですかねw
では、いつもながらドキュメントを
class sklearn.cluster.DBSCAN(eps=0.5, *, min_samples=5, metric='euclidean', metric_params=None, algorithm='auto', leaf_size=30, p=None, n_jobs=None)
eps, min_samplesは先程紹介したε、MinPtsに対応
algorithm: 近傍の距離の測定方法や見つけ方に種類がありその測定方法を指定できます。(例えばball_treeなどは詳しくは不明なのですが、高速処理ができたりするそうです。)
leaf_size: ball_treeもしくはkd_tree選択時にleaf sizeを指定できます。(詳細はかなり込み入るため割愛しますが、メモリの節約など高速処理に貢献できるそうです)
p: ミンコフスキー距離におけるpの値(いわゆる1/p乗した距離。p=2はL2norm)
metric, metric_params, n_jobsは割愛します。
使い方は、kmeansやAgglomerativeClusteringとほぼ同じなので割愛します。
・DBSCANまとめと注意点
DBSCANは一見有能そうに見えますが、実は欠点があります。
特にユークリッド距離を用いている時に顕著であり、それは次元の呪いという問題です。
機械学習で扱う特徴量の数はえてして膨大になり、次元数が増えていくと正確に一般化するために必要な訓練データ量が指数関数的に増えてしまうという問題です。
これは DBSCANだけに限らず、kmeans や階層クラスタリングでも起こりますが、DBSCANにはそれに加えて、εやMinPtsの数をうまく調整しなければいけないという問題も起こります。
例えば、先程のコードはある程度出来レースでしたが、epsやmin_samplesを極端にしてみましょう、
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=10.0, min_samples=100, metric='euclidean')
y_db = db.fit_predict(X)
plt.scatter(X[y_db==0, 0], X[y_db==0, 1], color='green', marker='*')
plt.scatter(X[y_db==1, 0], X[y_db==1, 1], color='blue', marker='s')
plt.title('DBSCAN')
plt.tight_layout()
plt.show()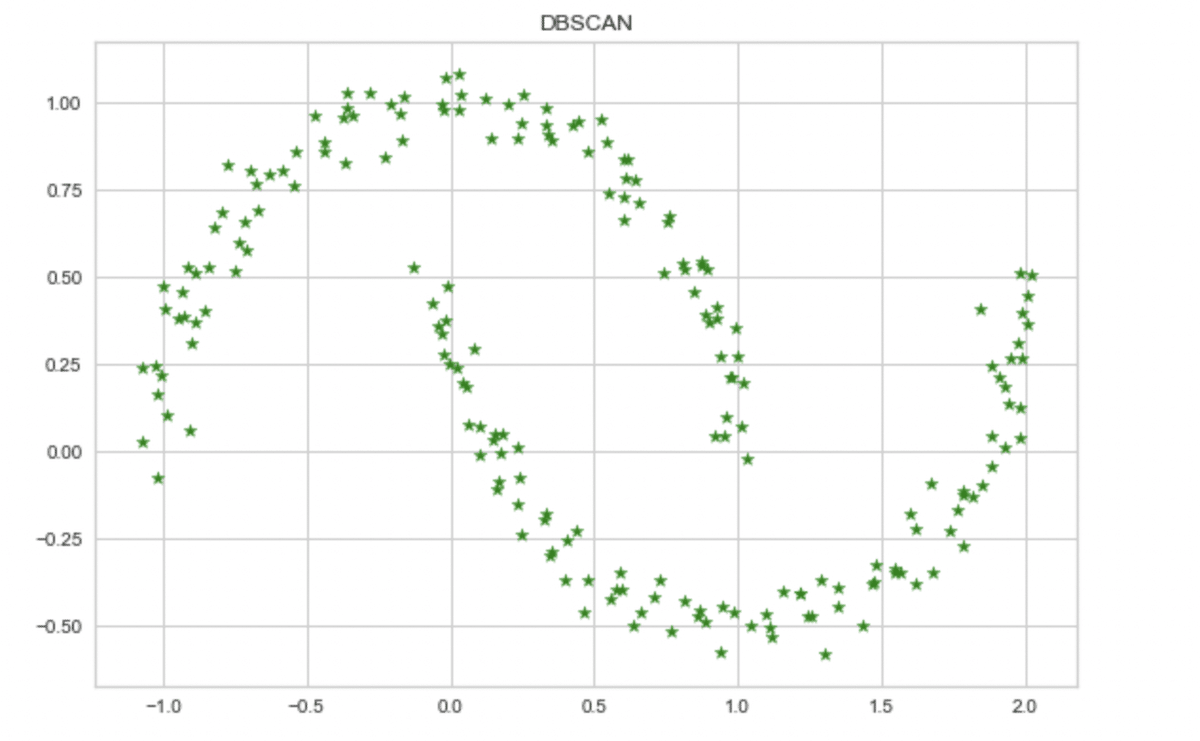
このように大きすぎる値を取れば全て同じクラスタリングになったりします。
また、kmeansのときから言っているように、最初からデータの分布がわかっているケースはほとんどなく、どのようにクラスタリングすべきかということは探り探りでないとわからないという現状を意識しておかなければいけません。
次元の呪いなどは主成分分析などでの抑制やいろんなアプローチはあり、2次元に圧縮することで可視化できるなどの特徴があるため、ぜひいろんなデータで今回の内容を生かしてみましょう!
・(appendix)スペクトラルクラスタリング
最後にもう一つのクラスタリングアルゴリズムである「スペクトラルクラスタリング」についてほんとに最初だけ解説して終わろうと思います。
クラスタ間の中心点からの距離ではなく、連結性に着目してクラスタリングすることが特徴的です。
具体的なアルゴリズムは避けますが、行列の固有値を求め、連結成分の分解を行っていきます・・・
以下のサイトが参考になります。
少しだけ実装もしておきます。( ちなみにwarningが出ているので、正しいコードというわけではないです。。)
from sklearn.cluster import SpectralClustering
sp = SpectralClustering(n_clusters=2, affinity='nearest_neighbors')
y_sp = sp.fit_predict(X)
plt.scatter(X[y_sp==0, 0], X[y_sp==0, 1], color='green', marker='*')
plt.scatter(X[y_sp==1, 0], X[y_sp==1, 1], color='blue', marker='s')
plt.title('SpectralClustering')
plt.tight_layout()
plt.show()
公式ドキュメント
https://scikit-learn.org/stable/modules/generated/sklearn.cluster.SpectralClustering.html
内容は割愛しますが、上記コードではうまくいきましたね!
・おわり
ってなわけで今回は終わりにします。
次回からNLP(自然言語処理)を扱っていこうと思いますが、参考書籍の自然言語処理がかなり個人的にイマイチなので、ほんとの基礎からBERTとか100本ノックとかにも対応させて充実させようかなと思っています。
では、また次回!
