機械学習〜さまざまなモデル性能評価の指標などなど

前回の続きです。。

・性能評価のさまざまな指標

前回までは、モデルの評価などにはcross_val_scoreなどで'accuracy（正解率）'を中心に評価してきましたが実際には複数の種類が存在します。

純粋に正解している率を知りたいときもあれば、
「正解と判断したうち、どのくらい間違っているのか？（適合率）」の方を気にするときもあります。

こういう、さまざまな性能評価指標に関して今回は見ていきましょう。

・混同行列（confusion matrix）

モデルの性能評価をする際に、前提となる混同行列というものの理解から始めます。

まずは、図で見ていきましょう。

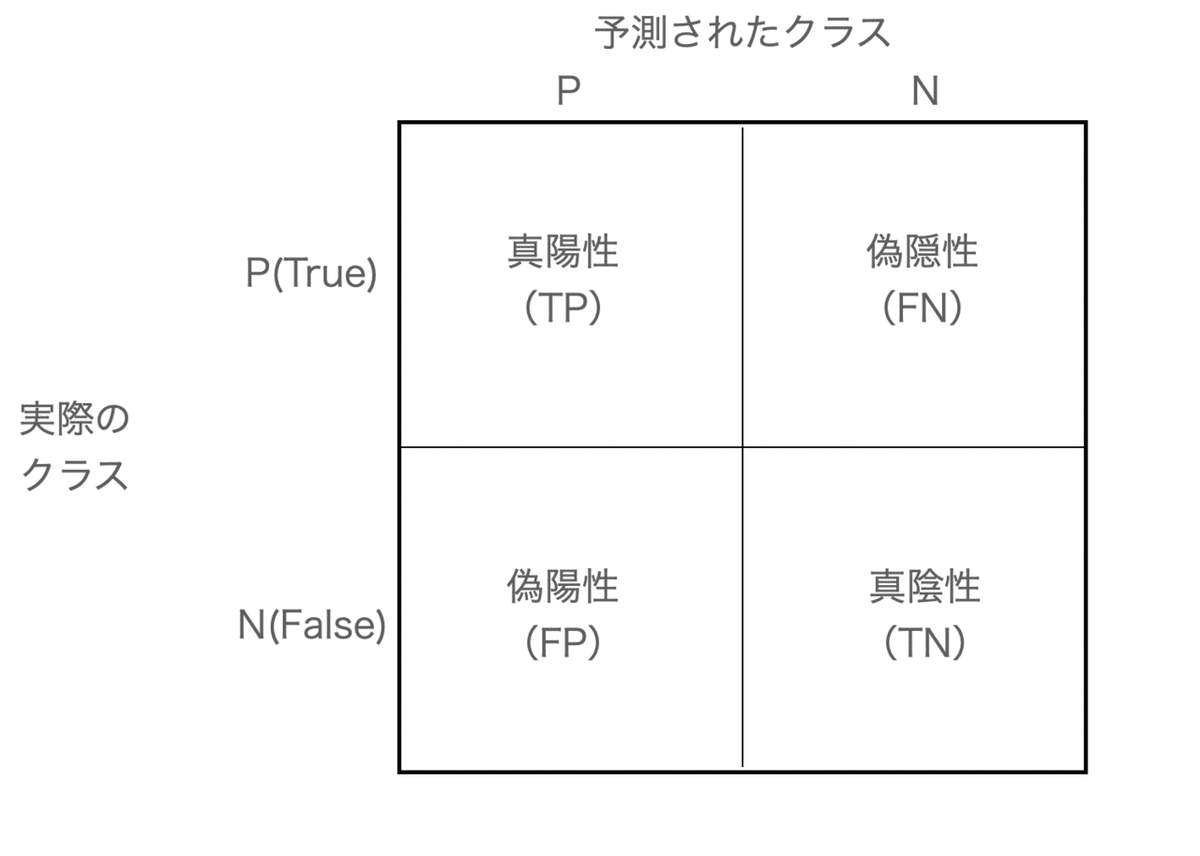
予測と実際の正解をマトリクスで示しています。

混同行列は上記の4つ
・真陽性（実際に真実でかつ正解）
・真陰性（実際には正しいが不正解と判断）
・偽陽性（実際には正しくないのに、正解と判断）
・真陰性（実際に正しくなく、かつ不正解と判断できている）

この辺は、数学の検定などにも共通していますね。

・Pythonで混同行列を実装

では、混同行列をpythonで書いていきます。

from sklearn.metrics import confusion_matrix

pipe_svc.fit(X_train, y_train)
y_pred = pipe_svc.predict(X_test)

confmat = confusion_matrix(y_pred=y_pred, y_true=y_test)
confmat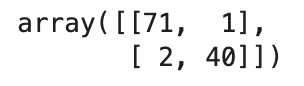

（おまけ　前回モデル比較でできたDecision Tree Classifierや、ランダムサーチで行ったpipe_svcのConfusion Matrixも見ておきましょう。※ランダムサーチはランダムに組み合わすため、毎度精度が異なります）

from sklearn.metrics import confusion_matrix

clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)

confmat = confusion_matrix(y_pred=y_pred, y_true=y_test)
confmat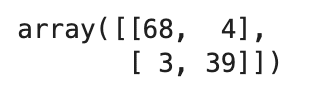

from sklearn.model_selection import RandomizedSearchCV
from sklearn.svm import SVC


param_distributions = [
   {'svc__C': param_range, 'svc__kernel': ['linear']},
   {'svc__C': param_range, 'svc__gamma': param_range, 'svc__kernel': ['rbf']}
]

rs = RandomizedSearchCV(estimator=pipe_svc, 
                param_distributions=param_distributions,
                scoring='accuracy', n_iter=10,
                cv=10, n_jobs=1, refit=True)

rs = rs.fit(X_train, y_train)
y_pred = rs.predict(X_test)

confmat = confusion_matrix(y_pred=y_pred, y_true=y_test)
confmat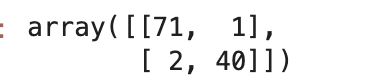

結果の見方に関しては、図と同じ順番で見ていただければ大丈夫です。

では、コードの説明を。公式ドキュメントにて。

sklearn.metrics.confusion_matrix(y_true, y_pred, *, labels=None, sample_weight=None, normalize=None)

y_true: array形式で正解の目的変数を格納
y_pred: predictメソッドなどで推定した予測リストを格納

labels: リストを指定することで、混同行列をリストの名前順にソート（通常はy_trueやy_predなどが使われる）

sample_weight: サンプルの重み（array形式）

normalize: {‘true’, ‘pred’, ‘all’} もしくはデフォルトでNoneを指定。true（列）もしくはpredict(row)もしくはその両方を標準化して表示したい時に利用。

返り値に関してはarray形式で各個数（厳密にはshape）が格納されています。

もう少し表示形式をいじってみて、わかりやすく表示するにはmatplotlib にあるmatshow関数を使います。

fig, ax = plt.subplots(figsize=(3, 4))
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)

rows = confmat.shape[0]
cols = confmat.shape[1]

for row in range(rows):
   for col in range(cols):
       ax.text(x=col, y=row, s=confmat[row, col], va='center', ha='center')

plt.title("SVM's Confusion Matrix")
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.tight_layout()
plt.show()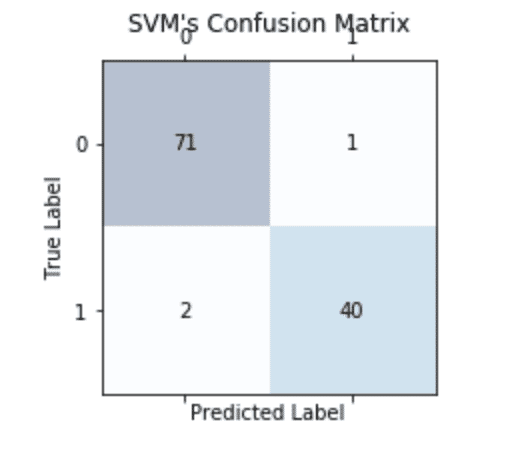

（ちょっと補足）
matplotlib.pyplot.textにて
s: 表示したい文字をstrで指定
va (vertical alignment): 文字の位置を平行線上としてどこに来るか指定（centerであれば、真ん中に平行線を引いてそこに文字が置かれるイメージ）
ha（horizontal alignment）: vaの垂直Ver（こんかいは両方centerなので、数値が真ん中に表示されている）

・誤分類率（ERR）と正解率（ACC）

さて、上記のSVMではFN=71、TP=40（confusion_matrixでlabels=Noneのため順番に注意！）という正解が出ましたが、実際にこれらの数値がどのくらい良いのかなどを測るための指標がいくつか存在します。

順に追って解説しますが、まずは誤分類率（ERR）と正解率（ACC）から。

- 誤分類率（ERR）

全ての総和（TP+TN+FP+FN）のうち、誤った予測（FP+FN）をしたものの割合を指します。

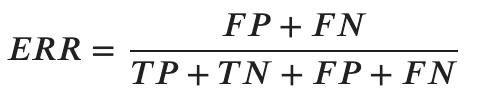
- 正解率（ACC）

正解率は1-ERRで算出できて、純粋に正しく正解できている割合です。

・真陽性率（TPR）と偽陽性率（FPR）

- 真陽性率（TPR）

次に、予測時はPositiveと判断したうち、どのくらいが本当にPositive（True）だったのかを測る指標が真陽性率です。

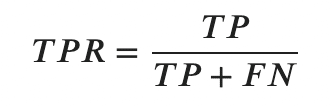
- 偽陽性率（FPR）

その反対に、実際はNegative（False）なのに、Positive と予測してしまった割合を偽陽性率と言います。

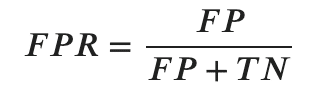
これらの指標は主に、医療や工場の検知などの不均衡なクラス（クラスが偏っていること。全体を見ると健康な人が多いけれど、一部の人は病気になるなど）に使われていることが多いです。

今回の悪性腫瘍の場合、当然ながら発見する（Positive）ことが必要ですが、実際には健康体であるにもかかわらず、Positiveと判断されてしまうこともまた問題なわけです。

このため、FPRの数値を減らすという施策も正解率を上げるのと同じくらい重要なときもあります。

・適合率と再現率

適合率とはPositiveと予測したうち、どのくらい本当にPositiveだったのかを示す指標です。

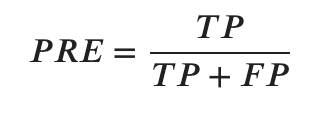
再現率（recall rate）とはTPR（真陽性率）の同義語（なぜに別な用語なのだろうか？？w）です。（式は割愛。）

再現率（真陽性率）を上げることはTPの値を大きくするつまり、本当はPositiveなのに、Negative と判断されることを防ぐことに繋がります。

しかしながら、そうすると今度はFP（病気でないのに病気である）と診断されるリスクが上がってしまいます。

つまり、適合率がよくなくなります。

そして、適合率をよくしようとすれば、今度は再現率が悪くなります。。

どうすればよいのか？

これを解決するのが、F1スコアと呼ばれる指標です。

式を先に見てみましょう。

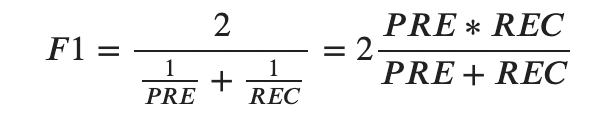
これは調和平均というやや特殊な平均が用いられています。

（ある距離を往復した時の平均時速を求めるときなんかに使われます。）

これによって、お互いの短所長所のバランスを取ることができるようになります。

・PythonでF1スコアを見てみる

from sklearn.metrics import precision_score
from sklearn.metrics import f1_score
from sklearn.metrics import recall_score


print(f'Precision: {precision_score(y_true=y_test, y_pred=y_pred):.3f}')
print(f'Recall: {recall_score(y_true=y_test, y_pred=y_pred):.3f}')
print(f'F1 score: {f1_score(y_true=y_test, y_pred=y_pred):.3f}')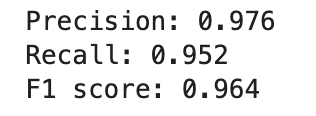

では、公式ドキュメントより。（上の3つのパラメータはほぼ同じなので、代表して、f1_scoreのパラメータの解説にとどめます。）

sklearn.metrics.f1_score(y_true, y_pred, *, labels=None, pos_label=1, average='binary', sample_weight=None, zero_division='warn')

- y_true, y_pred, labels, sample_weightはconfusion_matrixと同じ。

- pos_label: str or intで指定（default=1）例えば、=0  をpositiveにしたりできる。これにより、多少結果が変わることもある。
また、average~!='binary'でpos_label=[pos_label]とすれば、指定したpos_labelのみのスコアを算出できる

- average: {‘micro’, ‘macro’, ‘samples’,’weighted’, ‘binary’} もしくはNoneで指定。 defaultは’binary’。平均の方法（マクロ平均など）
参考サイト：https://note.nkmk.me/python-sklearn-confusion-matrix-score/

- zero_division: 0 devision（0が分母に来る時）のvalueを指定するかどうか（デフォルトはwarn）

・再度GridSearchCVを使って、性能指標もアレンジ

前回までで使ってきた、GridSearchCVにはscoringのパラメータで指定した性能を評価することもできます。今回はpos_label=0（陽性を0として指定）などをして結果を見てみましょう。

from sklearn.metrics import make_scorer, f1_score

pipe_svc = make_pipeline(StandardScaler(), SVC(random_state=1))

c_gamma_range = [0.01, 0.1, 1.0, 10.0]
param_grid = [
   {'svc__C': c_gamma_range, 'svc__kernel': ['linear']},
   {'svc__C': c_gamma_range, 'svc__gamma': c_gamma_range, 'svc__kernel': ['rbf']}
]

scorer = make_scorer(f1_score, pos_label=0)

# ハイパーパラメータの値のgridを指定して、
# グリッドサーチを行う
gs = GridSearchCV(estimator=pipe_svc, 
                param_grid=param_grid,
                scoring=scorer,
                cv=10, n_jobs=1)
gs = gs.fit(X_train, y_train)

print(f'Grid Search F1 score is {gs.best_score_}')
print(f'Best Param is {gs.best_params_}')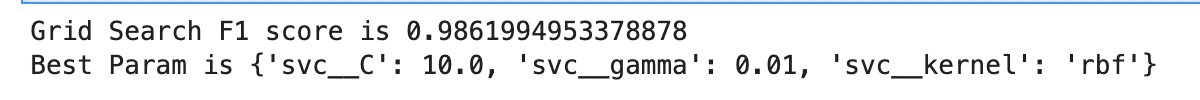

（基本的なコードはほぼ同じなので、説明は割愛）

・ROC曲線をプロットしていく

・ROC曲線とは？

さて、ここではROC曲線というものを見ていきます。（Receiver Operatorating Characteristic curve　受信者操作特性やらなんやらですが、ROC曲線、でおけだと思います。）

x軸にFPR（偽陽性率）、y軸にTPR（真陽性率）をとり、線をプロットしていくグラフですが、医療現場ではそれぞれ、「1 - 特異度」、「感度」と表現したりします。

何に使えるのか？と言われれば、分類モデルの選択の指標として、この後出てくるAUCの値が高いものを選ぶために使われます。

・・・ちょっとまだ不明瞭・・・・・・・・

一旦、図で可視化してみましょう。

このように、ROC曲線はそれぞれのPOINTでのTPR、FPRをプロットしたもので、その下の面積がAUCと言われています。

AUCが1に近ければ近いほどそのモデルの性能は良いとされ性能の指標として広く扱われています。

ざっくりと図で説明するとこーなります。

（ROC曲線の説明がどの参考書も硬いと感じていた（そして、個人的にわかりにくい）ので、なるべく可視化してみました。）

閾値（しきいち。Threshold）をそれぞれ変えてみて、プロットしていったものがROC曲線です。

・ROC曲線をPythonでプロット！

なんとな〜く、性能指標のひとつなんだ〜くらいの理解ができたところで、実際にROC曲線を書いてみて、より理解を深めていきましょう。

では、コードから。（めちゃ長い。。。）

from scipy import interp
from sklearn.metrics import roc_curve, auc


# 今回はスケーリング、主成分、ロジスティック回帰でpipeline
pipe_lr = make_pipeline(StandardScaler(),
                      PCA(n_components=2), 
                      LogisticRegression(penalty='l2', random_state=1, C=100))

# 特徴量を2つのみ取り出して、プロットをする
X_train2 = X_train[:, [4, 14]]

# StratifiedKFoldで3分割し、リストに要素を格納
cv = list(StratifiedKFold(n_splits=3).split(X_train2, y_train))

# プロットの準備
fig = plt.figure(figsize=(7, 5))

# TPRの平均値を算出するための初期化
mean_tpr = 0

# 0~1までの　１００の要素を生成
mean_fpr = np.linspace(0, 1, 100)

# それぞれのTRPの数値を格納するためのリスト
all_tpr = []

for k, (train, test) in enumerate(cv):
   # 各要素で学習
   # 学習したモデルに対し、predict_probaで確率を予測
   # predict_probaにより、今回n行x2列が返り、それぞれ[0, 1]に属する確率が[p, 1-p]で格納される
   probas = pipe_lr.fit(X_train2[train], y_train[train]).predict_proba(X_train2[test])
   
   # roc_curveでプロット
   fpr, tpr, thresholds = roc_curve(y_train[test], probas[:, 1], pos_label=1)
   
   # X軸、　Y軸を線形補完
   mean_tpr += interp(mean_fpr, fpr, tpr)
   
   mean_tpr[0] = 0.0
   
   roc_auc = auc(fpr, tpr)
   
   # plot
   plt.plot(fpr, tpr, label=f'ROC fold: {k+1} (area={roc_auc:.2f})')
   
# 当て推量をプロット
plt.plot([0, 1], [0, 1], linestyle='--', color=(0.6, 0.6, 0.6), label='Random guessing')

# FRP, TRP, ROC, AUCそれぞれの平均を計算
mean_tpr /= len(cv)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)

# plot
plt.plot(mean_fpr, mean_tpr, 'k--', label=f'Mean ROC (area={mean_auc:2f})', lw=2)

# 完全なる正解の時のプロット
plt.plot([0, 0, 1], [0, 1, 1], linestyle=':', color='black', label='Prefect perfomance')

# グラフのオプション
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend()
plt.tight_layout()
plt.show()

かなり長いので、割と詳細に何しているのかを説明できたらなと思います。

pipe_lr = make_pipeline(StandardScaler(),
                      PCA(n_components=2), 
                      LogisticRegression(penalty='l2', random_state=1, C=100))

まずは、これまで扱ってきたmake_pipelineで
標準化→PCA（主成分分析。2次元に圧縮）→ロジスティック回帰（l2正則化により、過学習を抑える）

X_train2 = X_train[:, [4, 14]]

今回は特徴量を2個のみピックアップして学習をする（今回、ROC曲線をみやすくしているだけで、本来は必要ありません。）

cv = list(StratifiedKFold(n_splits=3).split(X_train2, y_train))

また、今回のk分割交差検証に用いる値も少し小さくしています。（これもこちらの都合上。本来はいつも通りの5, 10でおけです。）

# プロットの準備
fig = plt.figure(figsize=(7, 5))

# TPRの平均値を算出するための初期化
mean_tpr = 0

# 0~1までの　１００の要素を生成
mean_fpr = np.linspace(0, 1, 100)

# それぞれのTRPの数値を格納するためのリスト
all_tpr = []

この辺は、プロットのための準備ですので、一旦説明は割愛。

さて、forループの中身を除いていきます。

   # 各要素で学習
   # 学習したモデルに対し、predict_probaで確率を予測
   # predict_probaにより、今回n行x2列が返り、それぞれ[0, 1]に属する確率が[p, 1-p]で格納される
   probas = pipe_lr.fit(X_train2[train], y_train[train]).predict_proba(X_train2[test])

pipelineでするため、fitメソッドを用いて、その後、predict_probaメソッドでX_train2[test]からyを予測し、[0, 1]に振り分けられる確率をリスト形式で格納していきます。

    # roc_curveでプロット
   fpr, tpr, thresholds = roc_curve(y_train[test], probas[:, 1], pos_label=1)

さて、本題のROC曲線の関数。

まずは公式ドキュメントより。

sklearn.metrics.roc_curve(y_true, y_score, *, pos_label=None, sample_weight=None, drop_intermediate=True)

y_true: ndarray形式で正解の目的変数を格納（基本は[0, 1] or [-1, 1]、それ以外の場合、pos_labelで指定が必要）
y_score: ndarray形式で目的変数を推定した確率を指定。（今回で言えばprobasの2列目（=probas[:, 1]））
pos_label: 目的変数が[0, 1] or [-1, 1]でないとき、指定が必要
sample_weight: サンプルの重み
drop_intermediate: ROC曲線のプロットの際に、thresholdの点線などを非表示にするかどうか（デフォルトはTrue）

返り値は以下。

fpr: FPRの値
tpr: TPRの値
thresholds: 閾値の値（徐々に値を下げていく。）初期値はmax(y_score)+1からスタート

(k=i回目の時のそれぞれの値を3つほど取り出してみると以下。)

# X軸、　Y軸を線形補完
mean_tpr += interp(mean_fpr, fpr, tpr)

今回、scipyからinterpをインポートしていますが、公式ドキュメントはなく、numpyからのインポートが良いもしくはscipy のinterpolateをインポートする方が良いと思います。

scipyとnumpyには同じ関数が格納されていますが、future warningなどでnumpyの方の関数を使ってくださいと出ることが多いので、こちらもnumpyを利用する方が良いのかなと個人的主観で思ったりしております。

numpy.interp(x, xp, fp, left=None, right=None, period=None)

空間xを（xp, fp）を通るように線形補完します。

k=0の時の線形補完したmean_tprを見てみると以下。

数値を見たところで感もありますが、0~1を100等分した空間を(fpr, tpr)を通る直線で補完しています。

すこし、次元を下げて考えると、以下の図のようなイメージとなります。

返り値は空間と同じshapeで補完された数値が返ってきます。

今回は、np.linspace(0, 1, 100)の空間に（fpr, tpr）を通る線形で補完して、返ってくる値は、補完されたtprの値と考えます。

mean_tpr[0] = 0.0

ROC曲線は必ず(0, 0）、(1, 1)を通るため、調整しています。

roc_auc = auc(fpr, tpr)

ここで、AUCの値を計算します。

公式ドキュメントより。

sklearn.metrics.auc(x, y)

x, y = fpr, tprです。また、返り値は面積の数値が返ってきます。

その後、各k=i 番目にてROC曲線をプロットしています。

次に、全体の平均をプロットするための準備をしています。

# FRP, TRP, ROC, AUCそれぞれの平均を計算
mean_tpr /= len(cv)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)

今、mean_tprに関しては、k=1, 2, 3回目の線形補完済みのtprが加算された状態であるため、平均するためにlen(cv) （=3）で割っています。

また、ROC曲線は(1, 1)を通るため、最後の要素は必ず1となります。

そして、auc関数でfpr, tprの平均した座標にて面積を算出。

これらをプロットして、最後に描画のオプションで見やすくしたのが出力結果となっています。

・（脱線）AUCの値のみ必要な時

ちなみに、プロットが不要でAUCのみ知りたい時は、以下でサクッとできます

from numpy import interp
from sklearn.metrics import roc_curve, auc, roc_auc_score


# 今回はスケーリング、主成分、ロジスティック回帰でpipeline
pipe_lr = make_pipeline(StandardScaler(),
                      PCA(n_components=2), 
                      LogisticRegression(penalty='l2', random_state=1, C=100))

# 特徴量を2つのみ取り出して、プロットをする
X_train2 = X_train[:, [4, 14]]

# StratifiedKFoldで3分割し、リストに要素を格納
cv = list(StratifiedKFold(n_splits=3).split(X_train2, y_train))

mean_auc = []

for k, (train, test) in enumerate(cv):
   # 各要素で学習
   # 学習したモデルに対し、predict_probaで確率を予測
   # predict_probaにより、今回n行x2列が返り、それぞれ[0, 1]に属する確率が[p, 1-p]で格納される
   probas = pipe_lr.fit(X_train2[train], y_train[train]).predict_proba(X_train2[test])
   
   auc_score = roc_auc_score(y_train[test], probas[:, 1])
   
   print(f'auc_score fold {k+1} is {auc_score:.2f}')
   
   mean_auc.append(auc_score)
   
   
print(f'Mean AUC Score is {np.mean(mean_auc):.3f}')

（本筋ではないため、軽く）

公式ドキュメントにて。

sklearn.metrics.roc_auc_score(y_true, y_score, *, average='macro', sample_weight=None, max_fpr=None, multi_class='raise', labels=None)

y_true, y_score, sample_weight, average, labelsなどは以前までのparameterと共通のため、割愛

max_fpr: 多クラス分類の際に利用
multi_class: 多クラス分類の際に利用。{‘raise’, ‘ovr’, ‘ovo’}で指定。One vs Restなど、多クラス特有の話なので、一旦飛ばします。

・多クラス分類のとき

いよいよ残り2テーマとなりました。

さて、今までは0, 1の二値分類を取り扱ってきましたが、実際には多クラスで分類するケースもたくさんあります。

多クラスにおいても、sklearnにはすでにaverageパラメータにより、さまざまな問題において拡張できるようになっています。

ここで、多クラス分類において、マクロ(macro)平均・マイクロ(micro)平均というものを先に解説します。

例えば、PRE（適合率）のmicro平均は全てのTPi, FPiの総和のうち、TPiの総和の割合を表します。

しかし、マクロ平均は、それぞれのPREiを求めた上でそれを算術平均したものを指します。

sklearnのaverageパラメータのデフォルトはmacroであるように、直感的にはmacroがわかりやすいかと思います。

マイクロ平均が役立つのは、全ての真陽性の値に対して平等な重みづけをしたい時です。反対に、一部の真陽性の数が圧倒的に多い場合は、ほとんどそのクラスの影響を受けてしまうことにもなります。

・クラスの不均衡

初めの回にsplitのstratifyなどで偏ったデータの分割に対処する必要があるとううことをちらほら書きました。

たとえば、100枚の画像のうち90枚が犬の画像であり、「とにかく犬と判定する」というアルゴリズムを組むとそれだけで正解率90% となってしまいます。

こういう状況の場合、モデルは学習したとは言えません。

ここでは、そういう偏った状況で正しく学習を行うためのアプローチを解説します。

まずは不均衡なデータの準備から。

X_imb = np.vstack((X[y == 0], X[y == 1][:40]))
y_imb = np.hstack((y[y == 0], y[y == 1][:40]))
print(X_imb.shape)
print(y_imb.shape)

np.vstackは、引数の配列を垂直方向に連結する関数です。(hstackは横方向)

本筋から逸れるので割愛しますが、こちらが参考になります。

このデータにはPositiveのデータが40個しかなく、357個はNegativeデータとなり、すべてを0（Negative）と予測すればそれだけで90%以上の正解率がでます。

y_pred = np.zeros(X_imb.shape[0])
np.mean(y_pred == y_imb ) * 100

こうした状況では単に正解率を見るだけではなく、適合率や再現率などを見るなどの他の性能指標も合わせてみることがお勧めされます。

また、正則化のように、少数派クラスの予測を誤ったときのペナルティを大きくすることで調整することも対処の一つとなります。

sklearnにはこの不均衡なクラスデータセットを調整するresample関数というものがあります。

試しに見てみましょう。

from sklearn.utils import resample


print(f'Number of class 1 examples before: {X_imb[y_imb == 1].shape[0]}')

X_upsampled, y_upsampled = resample(X_imb[y_imb == 1],
                                  y_imb[y_imb == 1],
                                  replace=True,
                                  n_samples=X_imb[y_imb == 0].shape[0],
                                  random_state=123)

print(f'Number of class 1 examples after: {X_upsampled.shape[0]}')

このように、1クラスをもつサンプルを0クラスと同じになるまで復元抽出しています。（復元抽出のため、一度取り出したものがまた出てくることもある）

実際にこれを使って先ほどと同じように全て0と予測しても50%にしかならないことが確認できます。

X_bal = np.vstack((X[y == 0], X_upsampled))
y_bal = np.hstack((y[y == 0], y_upsampled))
print(X_bal.shape)
print(y_bal.shape)


y_pred = np.zeros(X_bal.shape[0])
np.mean(y_pred == y_bal ) * 100

では、ラストの公式ドキュメントを見ていきましょう。

sklearn.utils.resample(*arrays, replace=True, n_samples=None, random_state=None, stratify=None)

*arrays: インデックス指定ができるarrayやリスト、DataFrameなども対応
replace: リサンプリングして実装するかどうか。Falseの場合、ランダムな順列で実装される。
n_samples: 指定した数だけサンプルが生成される
random_state: 省略
stratify: None以外の場合、指定した数値（shape）をクラスラベルとして階層化する（いわゆるk分割）

・おーーーわりっ！

ざっと振り返ります。

①毎度モデルの標準化やらPCAやらを行った後に推定器にいれて、、という処理をmake_pipelineで一括処理できる方法を学びました。

②データセットが少ない時や、モデルの性能をあげるためにk分割交差検証により、最適なハイパーパラメータを選ぶモデル選択やその評価を扱ってきました。

③グリッドサーチにより、しらみつぶしに最適なハイパーパラメータの組み合わせを見つける方法を学びました。

④性能の指標として、適合率や再現率、F1スコアにより、さまざまな角度からモデルの性能について理解し、最適化する方法を学びました。

⑤最後に、不均衡なクラスをもつデータセットの取り扱いに対するアプローチの基礎を学びました。

・・・

盛り沢山な内容で、非常に長い長い投稿になりましたが、これを元にさらに飛躍していきましょう！

では、また次回！