バギング・アダブーストでアンサンブル分類器を構築していく。

前回ではアンサンブル学習について学び、複数の異なる分類器を集めて大きな分類器として扱うことで、一つ一つの分類器よりも精度の高い分類器を作れることを学びました。

さて、アンサンブル学習法にはいくつか種類があり、その中でもバギングとアダブーストに関して見ていきます。

ではいきましょう。

〜バギング〜

・バギングとは？？

（私も含めて）なんだよこれ？ってなっている方に、まずは外観から。

バギング = Bootstrap AGGregatING

の略称で、

個々の分類器がそれぞれ、訓練データからブートストラップ標本（※）を抽出して学習する手法です。

※ ブートストラップ標本
　ランダムな復元抽出。復元抽出とは取り出したサンプルをもとに戻してからもう一度サンプルを取り出す方法。つまり何回も同じサンプルを引くこともある。
　おみくじでいえば、前の人が引いたおみくじはもとに戻してまた次の人がくじを引く。

（余談）Bootstrapと聞くとJava Scriptをイメージされる方（私です）もいるかと思いますが、個人的には再利用性が高いという意味でつけられたのかな〜なんて思っています。。

図にすると上記のイメージになります。

ほとんどアンサンブル学習の時のイメージと変わらないかなと思います。

・バギングを実装する

では、このバギングを実装していきましょう！！

今回使用するデータはWineデータです。

前回まではurl形式で取得していましたが、ま、sklearnのdatasets使います。

それと、今回も少し簡素にするため、クラス1, 2のみを使うとして、特徴量も2つに絞ります（普通にしたい方は絞り込まなくておけです、もちろん）。

この辺はお馴染みなので、ざっと書いちゃいます。（いやいや、わかんないよって方は最初の投稿にtrain_test_splitの詳細を書いてたりします。）

import pandas as pd

from sklearn.datasets import load_wine


wine = load_wine()
df_wine = pd.DataFrame(wine.data, columns = wine.feature_names)

df_wine['Class_label'] = wine.target

df_wine = df_wine.query('Class_label != 0')

X = df_wine[['alcohol', 'od280/od315_of_diluted_wines']].values
y = df_wine['Class_label'].values

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder


le = LabelEncoder()
y = le.fit_transform(y)

X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.2, stratify=y, random_state=1)

データの準備ができたところで、早速バギングを使っていきます。

今回、ベースの分類器を決定木にします。

また、max_depth=Noneと設定することで、各ノードが純粋（分類した後に単一クラスのみある状態）になるまで分割を繰り返します。

では、コードを見ていきましょう。

from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier


tree = DecisionTreeClassifier(criterion='entropy', 
                            max_depth=None, 
                            random_state=1)

bag = BaggingClassifier(base_estimator=tree, 
                      n_estimators=500, 
                      max_samples=1.0, max_features=1, 
                      bootstrap=True, bootstrap_features=False, 
                      n_jobs=1, random_state=1)

DecisionTree~に関しては、前回非常に膨大に書き散らしているので、割愛します。

では、バギングの関数の説明を。

公式ドキュメントより。

class sklearn.ensemble.BaggingClassifier(base_estimator=None, n_estimators=10, *, max_samples=1.0, max_features=1.0, bootstrap=True, bootstrap_features=False, oob_score=False, warm_start=False, n_jobs=None, random_state=None, verbose=0)

base_estimator: データのランダムなサブセットを学習する基本的な推測器を指定。デフォルトはNoneで、この場合は、決定木（DecisionTreeClassifier）
が用いられる。

n_estimators: 推測器の数

max_samples: 各推定器が学習するサンプル数（floatであればmax_samples*X.shape[0]で計算）

max_features: 各推定器に与える特徴量の最大数

bootstrap: ブートストラップ標本で抽出するかどうか

bootstrap_features: 特徴量の選択をブーストラップ標本で抽出するかどうか

oob_score: bootstrap=Trueの時のみ使用可能。ブーストラップ標本の特性上、抽出されなかったサンプルがある（これをOOB out of bags）。このサンプル達に対して予測精度を研鑽するとアンサンブル学習自体の予測精度を検証できるためそれを出力したいかどうか

warm_start: fitメソッド呼び出し時に以前までの学習を再利用できる。

n_jobs, random_state, verboseは省略。

これらの推定器を用いて正解率を実際に比較してみましょう。

それぞれコードを一気に見ていきましょう！

from sklearn.metrics import accuracy_score

tree = tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)

tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)

print(f'{tree_train} / {tree_test}')

木が剪定されていないため、過剰学習がみて取れます。

では、バギングはどうか？？

bag = bag.fit(X_train, y_train)
y_train_pred = bag.predict(X_train)
y_test_pred = bag.predict(X_test)

print()

bag_train = accuracy_score(y_train, y_train_pred)
bag_test = accuracy_score(y_test, y_test_pred)

print(f'{bag_train} / {bag_test}')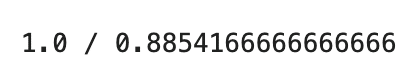

こちらの方が僅かながらに精度はいいもののそれでも過学習気味であります。

ちなみに、oob_score=Trueとして、実際にscoreを確認してみます。

bag_ = BaggingClassifier(base_estimator=tree, 
                      n_estimators=500, 
                      max_samples=1.0, max_features=1, 
                      bootstrap=True, bootstrap_features=False, 
                      n_jobs=1, random_state=1, oob_score=True)

bag_ = bag_.fit(X_train, y_train)
y_train_pred = bag_.predict(X_train)
y_test_pred = bag_.predict(X_test)

print(f'oob_score_: {bag_.oob_score_}')

bag_train = accuracy_score(y_train, y_train_pred)
bag_test = accuracy_score(y_test, y_test_pred)

print(f'{bag_train} / {bag_test}')

実際に、抽出されなかったサンプルに対しても高い精度であることがわかりますね！

- バギングとセットで聞くスタッキングとは？

詳しい方の中にはバギングと並行してスタッキングという方法も聞いたことがあります（私はなかったです。）

スタッキングはバギングの改良版と言える立ち位置で、

例えばブートストラップ標本で仮にすべて外れ値のようなサンプルを繰り返し取得してしまうことも当然ながら確率として起こり得ます。

そのような時に単純平均（いわゆる多数決）をしてしまうと偏りが生じることになります。

そう、前回の多数決でも出てきた重みをつけて加重平均をとって予測値を決めることをスタッキングと言います。

？？？

前回の多数決の重み付けとどう違うのか？

少し表現だけでは混乱を招きますので、図を用います。

先にいえば、スタッキングは階層を持つモデルと考えればおけです。

純粋に多数決をするのではなく、まず個々の分類器を用いて予測させたその値を特徴量として新たな分類器に入れて、その新しい分類器の予測値を最終的な予測値とするのがスタッキングです。

・スタッキングモデルを実装！

では、スタッキングモデルを実装してみます。

まずはコード。

from sklearn.ensemble import StackingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

estimators = [
   ('rf', RandomForestClassifier(n_estimators=10)),
   ('pipeline', Pipeline([
                           ('sc', StandardScaler()), 
                           ('linSVC', LinearSVC())
                           ]))
]


stack = StackingClassifier(estimators=estimators, 
                          final_estimator=LogisticRegression()
                         )

stack.fit(X_train, y_train)
y_train_pred = stack.predict(X_train)
y_test_pred = stack.predict(X_test)

y_train_score = accuracy_score(y_true=y_train, y_pred=y_train_pred)
y_test_score = accuracy_score(y_true=y_test, y_pred=y_test_pred)

print(f'Stacking score is {y_train_score:.3f} / {y_test_score:.3f}')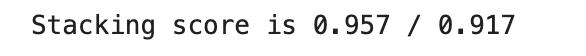

・バギングやスタッキングの決定領域を描画！

前回同様、描画していきます。

細かい説明などは部分的に説明しようと思います。

また、それぞれのshapeなどは適宜printすることでそれぞれの形がわかるかなと思います。

# 描画領域の準備
x_min = X_train[:, 0].min() - 1
x_max = X_train[:, 0].max() + 1
y_min = X_train[:, 1].min() - 1
y_max = X_train[:, 1].max() + 1

xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))

print(f'len(np.arange(x_min, x_max, 0.1)): {len(np.arange(x_min, x_max, 0.1))}')
print(f'len(np.arange(y_min, y_max, 0.1)): {len(np.arange(y_min, y_max, 0.1))}')
print(f'xx.shape: {xx.shape}')

fig, axes = plt.subplots(1, 3, sharex=True, sharey=True, figsize=(8, 3))

print(f'xx.ravel(): {xx.ravel()}')
print('-'*10)
print(f'np.c_[xx.ravel(), yy.ravel()]: {np.c_[xx.ravel(), yy.ravel()][:4]}')
print(f'np.c_[xx.ravel(), yy.ravel()].shape: {np.c_[xx.ravel(), yy.ravel()].shape}')


for idx, clf, title in zip([0, 1, 2], [tree, bag, stack], ['Decision Tree', 'Bagging', 'Stacking']):
   clf.fit(X_train, y_train)
   
   Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
   Z = Z.reshape(xx.shape)
   
   axes[idx].contourf(xx, yy, Z, alpha=0.3)
   axes[idx].scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], c='blue', marker='^')
   axes[idx].scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], c='green', marker='o')
   
   axes[idx].set_title(title)


axes[0].set_ylabel('Alcohol', fontsize=12)
plt.tight_layout()
plt.text(0, -0.2, s='od280/od315_of_diluted_wines', ha='center', va='center', fontsize=12, transform=axes[1].transAxes)
plt.show()

trainデータでの決定木とバギングは正解率1だったので、かなり過剰な領域の決め方をしていますが、スタッキングはかなり自然な領域で決定されることが見て取れますね。

----- 簡単な補足-----

前回説明を割愛したnumpy.meshgridの説明を少し。。

gridとあるように、格子状に並ぶような行列を作成するもので、

ざっくりとした図の作り方は以下のようになります。

それぞれの配列の要素数にて、xx, yyは(yの要素数, xの要素数)のshape（ややこしいですが、列のメモリがx軸に対応しているため、順番が反対になっています。。）

また、matplotlibのcontourfはそもそも等高線を意味し、値が同じものに対して線（または色塗り）を引きます。

contourf(格子点のx座標の配列, 格子点のy座標の配列, 値の配列)

の順に配置していきます。

今回、全て配列の形は揃えられているため、x, yの座標にZの値（今回、predictメソッドの出力結果のため0 or 1が格納）をプロットして描画します

（詳しい説明は割愛）

----- 簡単な補足おわり-----

・バギングまとめ

以上でバギングは一旦おしまいです

バギングはバリアンスの抑制に強く、単一の決定木のような過学習が起きやすい時に効果的です。

しかしながら、過小学習に対する抑制には対応できないことを考慮すべきであり、単体でバイアスがそもそも低いような分類器を剪定しておく必要があります。

〜アダブースト〜

・イントロ〜ブースティングとは？

アダブーストを学ぶ前にブースティングというそもそもの大枠を解説します。

先程のバギングでは、複数の分類器をそれぞれ同時に学習させ、多数決などで最終予測を決めました。

このブースティング（boosting）は、学習器を逐次的に訓練させていくことです。つまり、最初に学習器が分類した結果をもとに誤分類したデータに対する重みを大きくするなどの調整を行い、次の分類器に引きつぐ、、そしてこれを繰り返していくことをブースティングと言います。

また、個々の学習器に関しては弱学習器と言われる単純な学習器をベース分類器とすることも特徴的です。

ブースティングはアダブースト、勾配ブースティング（xgboostで実装）などが有名なので、アダブースト以外にも少し実装して行けたらと思います。

・ブースティングの仕組み

非常に大枠の手順は4つのみで構成されています。

1.
訓練データセットDからランダムに非復元抽出したサブセットd1を弱学習器C1で訓練
2.
次に同じDから再度非復元抽出したサブセットd2を用意し、1で誤分類されたデータ点の50%を追加して弱学習器C2で訓練
3.
DからC1, C2で結果が違う訓練データd3を洗い出して、3つ目の弱学習器C3で訓練
4.
弱学習器C1, C2, C3を多数決により組み合わせる

ブースティングはVariance・Biasともに低くなりますが、アダブーストに関してはVarianceが高い（過学習する）ことが知られています。

また、アダブーストに関しては、非復元抽出はせず、データセット全てを使うことが少し異なります。

では、アダブーストの外観を図で見てみましょう。（一気に説明します。）

まず一つ目の弱学習器で学習します。

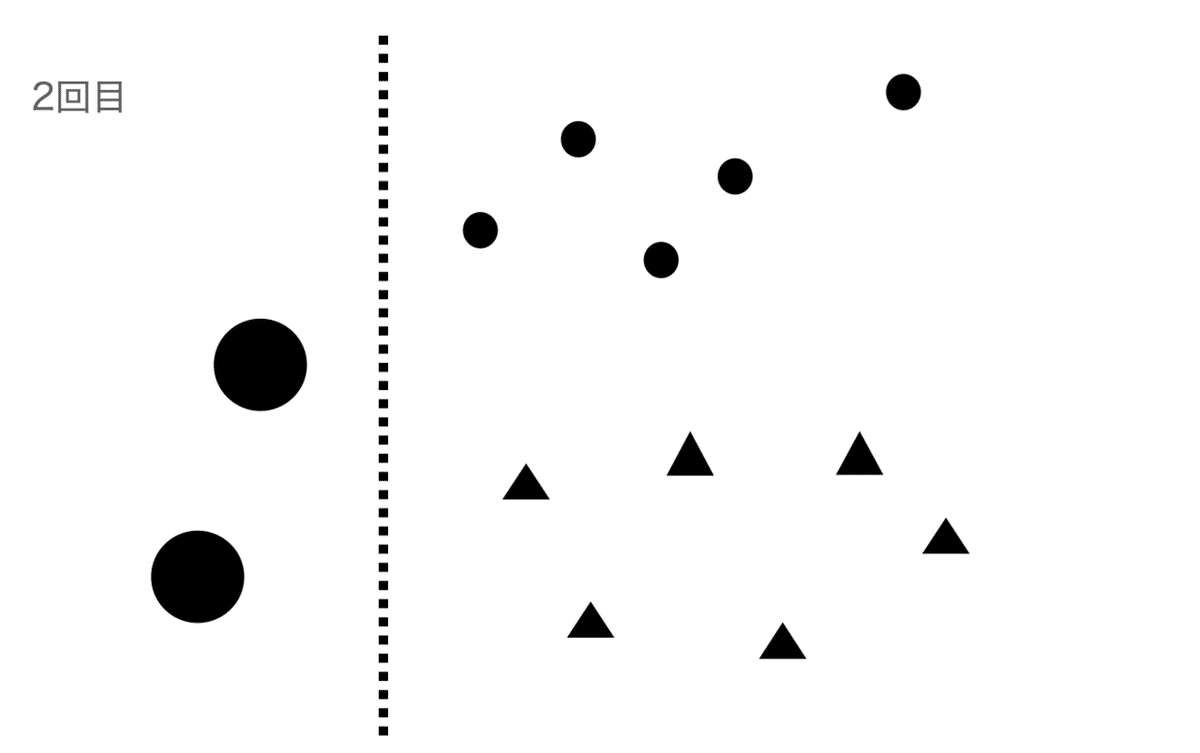
二回目を学習するときは、1回目で誤分類したデータに対して重みを大きく（円を大きく）、正解したものは小さくして学習します。

1, 2回目と同様誤分類したものは大きく、正解すれば小さくします。

3つの学習器で最終的な重みづけして多数決をとります。

・アダブーストを疑似コードや数式で解説

ここでは、アダブーストを数学の観点から掴んでいきます。

この数式などは覚える必要はなく、まずは流し見するくらいで十分です。

ここから少し数式が出てきますので、苦手な方は飛ばしていただいて構いません。（いつものことながら最小限の知識で済むように適宜解説は入れていくつもりです。。）

X: 訓練データセットの特徴量行列
y: クラスラベルのベクトル
w_j: j番目の重み（ベクトル）

としておきます。

1. まずは重みを等しく設定します。（サイズNのとき、w1 = 1/N）

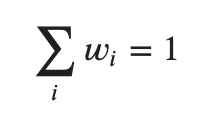
2. m回実行するブースティング操作のうち、j回目(=1~m)では以下a~fを繰り返して行います。

a. 重みw_jを用いて弱学習器Cjを訓練

　Cj = train(X, y, w_j)　※このtrainはpythonでいうfitのこと

b. クラスラベルy'を予測

　y' = predict(Cj, X)　※このpredictはpythonでいうpredict のこと

c. 誤分類率εを計算

　ε = w_j ・I(y' ≠ y)
- 「・」は行列の内積
- I(y' ≠ y)は指示関数で予測値が間違っていると1を返し、正解なら0を返す

d. 重み更新に用いる係数α_j を計算。

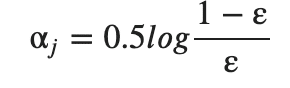
e. 重みの更新

w_(j+1) = w × exp(- α_j × I(y' ≠ y) )
- 「×」は対応する要素の乗算

f. w_(j+1)を正規化する

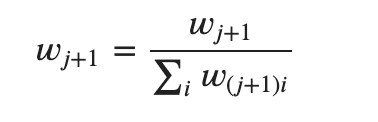
3. 最終的な予測y' を計算する。

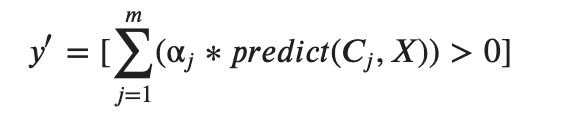
表現上、少し厳密な表記でなく、内容も厳密性がないため、あくまで参考程度ですが、ざっとみてきました。

・アダブーストをpythonで実装

では、いつもながらpythonでの実装に移ります。

先程のwineデータを引き続き利用します。

決定木単体での精度を確認。

from sklearn.ensemble import AdaBoostClassifier


tree = DecisionTreeClassifier(max_depth=1, criterion='entropy', random_state=1)

tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)

train_score = accuracy_score(y_true=y_train, y_pred=y_train_pred)
test_score = accuracy_score(y_true=y_test, y_pred=y_test_pred)

print(f'Accuracy scores are {train_score} / {test_score}')

コードの内容は既出のため割愛。

では、アダブーストの方をみます。

ada = AdaBoostClassifier(base_estimator=tree, n_estimators=500, learning_rate=0.1, random_state=1)


ada.fit(X_train, y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)

train_score = accuracy_score(y_true=y_train, y_pred=y_train_pred)
test_score = accuracy_score(y_true=y_test, y_pred=y_test_pred)

print(f'Accuracy scores are {train_score} / {test_score}')

なんと、今回は過剰学習をしてしまっていました。。（Varianceが高い。。）

解説の前に、念のため、GridSearchでn_estimators, learning_rateだけ変えてみて結果が変わるのか、どのパラメータが良さげなのか確認しておきます。

from sklearn.model_selection import GridSearchCV


grid_params = {'n_estimators': [50, 500, 1000], 'learning_rate': [0.01, 0.1, 1.0, 10.0]}

gs = GridSearchCV(AdaBoostClassifier(base_estimator=tree), param_grid=grid_params, scoring='accuracy')

gs.fit(X_train, y_train)
gs.score(X_test, y_test)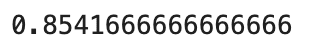

gs.best_params_

結局、推定器の数は50でよくて、learning_curveは0.1, 0.01でもそもそも過剰学習しちゃっているので、大した結果の差は出ませんでしたね。

では、AdaBoostClassifierの関数の解説に。

公式ドキュメントより

class sklearn.ensemble.AdaBoostClassifier(base_estimator=None, *, n_estimators=50, learning_rate=1.0, algorithm='SAMME.R', random_state=None)

base_estimator, random_stateに関しては既出のため割愛。

n_estimators: 推定器の最大数（今回で言えば500個のtree学習器を用意）

learning_rate: それぞれのブースティングのイテレーション時にそれぞれの分類器に適用する重みの設定。いわゆる学習率

algorithm: {‘SAMME’, ‘SAMME.R’}で指定。アルゴリズムになり、かなり込み入った話になるため割愛。

（余談）

参考にしているテキストは直接URLからデータを引っ張ってきているため結果が違っていて、テストデータの精度は単一の決定木よりもよかったです。。ふむ。。

・（appendix）他のブースティングを少しかじる。

最近のkaggleなんかを見るともっぱらlightGBMが目立ちますが、今回はxgboost、GradientBoostingClassifierを使ってみて、もう少しこのデータで練習でもしてみましょう。

特に詳細な説明はせずにコードと結果を参照するにとどめます。

ちなみに、勾配ブーストは前の学習器の残差に着目し重みの調整をするものです。

まずは勾配ブースティングから

from sklearn.ensemble import GradientBoostingClassifier


# パラメータはおよそadaboostと似たような数値を用いる
gb = GradientBoostingClassifier(n_estimators=500, learning_rate=0.1, max_depth=1, random_state=1)


gb.fit(X_train, y_train)
y_train_pred = gb.predict(X_train)
y_test_pred = gb.predict(X_test)

train_score = accuracy_score(y_true=y_train, y_pred=y_train_pred)
test_score = accuracy_score(y_true=y_test, y_pred=y_test_pred)

print(f'Accuracy scores are {train_score} / {test_score}')

・XGBoost（ちなみに、自分もまったくもって使い慣れてないので、公式サイトやいろんなサイトを参照してこぎつけたコードになります。）

import xgboost as xgb


xgb_train = xgb.DMatrix(X_train, label=y_train)
xgb_test = xgb.DMatrix(X_test, label=y_test)

xbg_param = {
   # 二値分類
   'objective': 'binary:logistic',
   # 決定木の深さ
   'max_depth':1,
   # 評価指標
   'eval_metric': 'logloss'
}

bst = xgb.train(xbg_param, xgb_train, num_boost_round=20)
preds = bst.predict(xgb_test)

# しきい値 0.5 で 0, 1 に丸める
y_pred = np.where(preds > 0.5, 1, 0)

accuracy_score(y_true=y_test, y_pred=y_pred)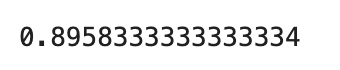

やはり、一番精度が高いのはXGBoostになりました。

- 決定領域を見てみる

最後は決定領域を見てこの記事を終了しましょう！

コードは既出なものが多いので、説明は割愛します。

# 描画領域の準備
x_min = X_train[:, 0].min() - 1
x_max = X_train[:, 0].max() + 1
y_min = X_train[:, 1].min() - 1
y_max = X_train[:, 1].max() + 1

xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))

fig, axes = plt.subplots(1, 2, sharex=True, sharey=True, figsize=(8, 3))

for idx, clf, title in zip([0, 1], [tree, ada], ['Decision Tree', 'Adaboost']):
   clf.fit(X_train, y_train)
   
   Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
   Z = Z.reshape(xx.shape)
   
   axes[idx].contourf(xx, yy, Z, alpha=0.3)
   axes[idx].scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], c='blue', marker='^')
   axes[idx].scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], c='green', marker='o')
   
   axes[idx].set_title(title)


axes[0].set_ylabel('Alcohol', fontsize=12)
plt.tight_layout()
plt.text(0, -0.2, s='od280/od315_of_diluted_wines', ha='center', va='center', fontsize=12, transform=axes[1].transAxes)
plt.show()

・まとめ

今回はアンサンブル学習のいくつかの種類、ブースティングまで見てきました。

アンサンブル学習は一つの分類器よりも精度は高くなりやすいですが、計算コストが高くなるため、どの程度の精度が必要なのかを加味し、それに見合うだけのリターンが得られるのかを考慮する必要があります。

一通りのアンサンブル学習の流れや外観に関しては理解が深まったのではないでしょうか？？（微妙でしょうか？w）

では、次回はクラスタリング（もしくは自然言語処理）について書く予定です！