機械学習の関数たち〜sigmoid, tanh, softmaxとか〜

tensorflowもなかなかに本格的になってきました。

次回以降seq2seqを扱い、次にtransformer, attention, BERTに行けたらと思います（ここから自分の理解も正しくしておかないとなので、時間かかりそぅ。。）

本格的始める前に、いままで扱わなかった機械学習の関数たちをちょっとだけみておくことにします。

noteで関数の表記をすることが非常に面倒で、
かえってわかりにくくなる可能性もあるな〜と思っているので、そのへんはご了承ください。

（あと、基礎的な部分しか書く予定がないので、すでに理解されている方はあまり有益でないと思いますw）

では、今回もよろしくお願いいたします。

・ロジスティック回帰

機械学習の基本として扱われるロジスティック回帰から始めます。

とはいっても、今回は理論を中心に扱いますため、
実装はない（もしくは図示するタイミングで少し）と思います。

ロジスティック回帰は「回帰」ですが、ほとんど分類に使われて、
確率を計算する関数のことになります。

sklearnとかでは大抵0, 1判定で使う印象があるかもしれませんが、そもそもは確率を意識された関数になります。

その前に「回帰」に使われる線形モデルから見ておきます

まず、身長から体重を予測したい場合、以下のような一般化が行われたりします

体重 = α + β * 身長

この辺は特に問題ないと思いますが、では身長を用いて服のサイズを予測したい場合、

服のサイズ = α + β * 身長

とは書けません。

服のサイズはS, M, Lや数値としても34, 36もしくは1, 2, 3, ...

みたいに離散分布しているため、線形では表現できません。

そこでロジスティック回帰の考え方が出てきます。

気温とダウンジャケットの販売数を考えてみます。

先程の服のサイズのように

ダウンジャケットの販売数 = α + β * 気温

気温に関してはマイナスの値も取りますし、不適切です。

ここで左辺にのみlog をとってみます

log(ダウンジャケットの販売数) = α + β * 気温

こうすると、実はうまく適応できるようになります。

logは関数としてマイナスもとりますから、右辺がマイナスでもうまく繋げることができます。

では、最初に確率を使う、という話がありましたが、どこから確率を用いるのでしょうか？

病気と喫煙時間の関係で見て行きます。

病気は「かかる(1) or かからない(0)」ですから、何度も書きますが、

病気(1, 0) = α + β * 喫煙時間

とは表現できません。

では、確率として

病気にかかる確率 = α + β * 喫煙時間

これもまだ不十分です

確率は0~1をとりますが、右辺は0未満、1より上になることもあります。

ここでロジット関数という得体の知れない関数を持ってきます。

＝＝＝＝
その前に準備としてオッズ比について先に解説します。

オッズ比とはある事象が起こる確率pを用いて

オッズ比 = p / (1 - p)

と表現できます。

言葉にすれば

「事象が起こる確率 ÷ 事象が起こらない確率」

もっと噛み砕くと

「事象が起こる確率は、起こらない確率に比べ何倍くらいあるの？」

ってことです。
＝＝＝＝

ここで、病気にかかる確率をpとして、

logit(p) = log( p / (1 - p) ) = α + β * x

と表現できるようになります。

今関心があるのはpですから、「p=」という形にすると

p = 1 / { 1 + exp(α + β * x) }

と書けることになり、α, βを最適化することが目標になりました。

大体の参考書の式が上のようになっていると思います。

==ちょっと補足==
ここからα,  β を「最適に」するとありますが、それは尤度関数を使って行って行きます。

P_n = (p_n ** tn) * {(1 - p_n)**(1 - tn)}

を用いて、

これをn=1~Nまで考えるわけですので、

L( β ) = ΠP_n

これが最大になるβを定めることを意味します。

（p_nはn人目の人が病気になる確率、tnは0, 1のみをとる。β = (β0, β1 )）

これを計算しやすく両辺にlogをとって計算しやすくすると

-logL( β ) = - Σ { tn *(p_n) + (1 - tn) *(1 - p_n)}

として、順に最適化プロセスを踏んでいきます（概要のみ掴みたいので残りは割愛）
==補足終わり==

このようにpという確率を求めるのが、いわばロジスティック回帰、って感じです。

・logistic sigmoid function （ロジスティックシグモイド関数）

では、よくみるシグモイド関数についてここから見て行きます。

シグモイド関数、とも言いますが、
実はロジスティックシグモイド関数が正式だったりします。

名前のようにロジスティック関数の特別なバージョンであり、

z = w0 + w1 * x1 + ... + wm * xm = W_T * x
(W_T は重み行列の転置)

として

φ(z) = sigmoid(z) = 1 / ( 1 + exp(-z) )

と表現されます。

上記の式を使うことがほとんどですが、式変形をして

φ(z)
= 1 / ( 1 + exp(-z) )
= exp(z) / ( 1 + exp(z) )
= exp(x / 2) / ( exp(x / 2) exp( - x / 2) )

とかを使っていくケースもあります。（基本的に最初の式だけで十分）

そもそもロジスティック回帰が確率を表現したいことから始まったように、logistic sigmoidも確率に関係しています。

ざっとlogistic sigmoidの関数の特徴だけ図で示しておきます。

sigmoidはφ: R -> (0, 1)というように、いかなる実数値も０~1の値にぎゅっとできるわけなので、確率としてみなせるようになります。

分岐点となるx = 0から右に行く（xが大きくなる）と、確率は1に近づき、左に行けば0になります。

x = 0 で確率1 / 2 となり確率50%です。

つまり、z = W_T * x において、sigmoidに渡せば出力される値は、
x（例えば病気にかかる確率などなど）の起こる確率として解釈できるようになります。

（ちなみに、多クラス分類は上記の通りでないことに注意。このときソフトマックス関数をつかいますが、後述）

ちょっとだけ派生すると

φ(z) + φ(-z) = 1

という性質があります。

これ、何いってるの？ってなると思うのですが、

要はφ(z)はx=0を境に対称な関数であることを示しています。（詳細は割愛）グラフを見てもそうっぽいよね〜くらいはわかるかなと思いますw

logistic sigmoidは二値分類においての確率である、
という話をしてきましたが、

ここでP(A) = φ(z) 　(Aが起こるという事象をP(A)としている)

とすれば、

P(not A) = 1- P(A) = 1 - φ(z) = φ(-z)

となるわけです。

要するにAの起こりやすさはzに関係し、Aの起こりにくさは-zである
って言えるわけです。

かなり確率と密接であることがイメージできたのではないでしょうか？？（どうでしょうw）

そして、先程みたオッズ比をもう一度見てみると

P(A) / P(not A) = φ(z) / 1 - φ(z) = φ(z) / φ(-z) = exp(z)

という綺麗な式に到達します。
（中の変換は割愛します。そこまで複雑ではないです。）

つまり、P(A)はexp(z)倍だけP(not A)よりもおこりやすい

って表現できます。

・tanh (hyperbolic tangent)

ではtanhについて見て行きます。

sigmoid関数とも非常に関係性のある関数です

GRUやLSTMでもtanh関数が使われていましたが、定義式は

tanh = ( exp(-z) - exp(z) ) / ( exp(-z) + exp(z) )

（みにくい。。）

これを少し変形すると

tanh(z) = ( sigmoid( z / 2 ) +1 ) * (1 /2)

になります。

（みっっにくい。。この変形も割愛します。手計算でも十分可能だとは思います、多分）

＝＝補足＝＝
tan(x), sin(x), cos(x)とかは高校数学でも扱いましたが、
tanh, sinh, coshとかもあり、tangentと同じく

tanh = cosh / sinh

の関係性が成り立ちます。

また、sin**2 + cos**2 = 1でしたが、

sinh**2 - cosh**2 = -1

となり、双曲線になることがわかります。
＝＝＝＝＝＝

数式での特徴が盛りだくさんなtanhであり、物理でも見かけるのですが、ここではそこまで踏み込まず進みます。 

tanhはsigmoid よりもとりうる値が広く(-1, 1)となります。

つまり負の値が大きいときに-1をとります。

これの何がいいのか？ということなんですが、

sigmoidの場合、zが非常に大きい負の数であるとき、限りなく0に近い値を取ってしまうので計算コストという部分で厄介なわけです。。

tanhであれば-1に近づくので計算も楽ちん！ってなります。

なので性質の違いを生かしてsigmoid とtanhが使い分けられたりしているのですね。

・softmax関数

ロジスティック回帰の部分で多クラスになるとロジスティック関数では不完全になる、みたいな話をしました。

多クラス分類においての所属確率が欲しいときはこのソフトマックス関数を使うことで対処できます

定義式を見ると

x = (x1, x2, ..., xn)にて

φ(x) =  exp(xi) / Σexp(xi) 

となります
（みにくい。。普通に他のサイトとかで綺麗に表記されているのは山ほどあるので、そちらを参考に。。）

もともとの要素をexpに乗っけていることから全て正の数値へ変換できるため、マイナスの要素であっても最終的に確率へ落とし込むことができます。

このφ(x) の要素全てを足し合わせると1になることから、
多クラスの確率と見なすことができるわけです。

とはいえ、まずn=2のときのsoftmax関数を見てみます

表記上作法とは違うのですが、x' = (x, y)とします

φ(x') = ( exp(x) / { exp(x) +exp(y) } , exp(y) / { exp(x) +exp(y) } )

となります。

ここで、exp(y - x) = z と変形してみると

φ(x') = ( sigmoid(-z), sigmoid(z) )

となります（急な展開ですが、こちらもゆっくり式変形すればわかります）

つまり、softmaxはsigmoidをより拡張したものと言えるわけです。

覚えてるかどうかわかりませんが、

sigmoid(z) + sigmoid(-z) =1 
※ここではφをsotfmaxとしているので、区別しやすいように「sigmoid」としました

だったことを思い出すと

φ(x') = ( sigmoid(-z), sigmoid(z) )

片方が大きければ、片方は小さくなり、ちゃんと確率として表されるわけです。

では、もう少しsoftmaxの性質を見て行きます。

そもそも入力ちから確率が出てくるため、実はその要素の大きさよりも差分がどのくらいあるのか？に関心があるのがこのsoftmaxとなります。

例を見て行きます。

今、ある定数cがあり、

φ(x + c) を考えます。

すると、

φ(x + c) =  exp(xi + c) / Σexp(xi + c) 

となり、

exp(x + c) = exp(x) * exp(c)とできることを利用すると

φ(x + c)
=  exp(xi + c) / Σexp(xi + c) 
= { exp(xi) * exp(c) } / Σ{ exp(xi) * exp(c) }
= { exp(xi) * exp(c) } /  exp(c) * Σexp(xi)
= exp(xi) / Σexp(xi)
（※exp(c)は約分）
= φ(x)

となります。

つまり、要素の大きさはあまり影響しないことがわかりました

・ReLU

では、最後ReLUを解説して終わります。

ReLU のほうがシンプルで、定義式は

φ(z) = max(0, z)

となります。

z <=0ではずっと0
z> 0なら恒等関数

これはsigmoidやtanhのように勾配（活性化関数の導関数の値）を考えるとき、極端に大きいところでの導関数の値は0に限りなく近づいてしまいます。

その場合、重みの更新がされなくなるために、学習ができなくなることがあります。

＝＝正しさを無視した例え話＝＝

この傾きが0になると、学習がされなくなるのか？ということですが、数式的に見れば勾配降下法の例を見てもわかるように

w := w - η * J'(z)

で更新されるため、このη * J'(z)部分が0 だと重みwはずっとwのままで進んでしまう、ことになります。

これを例えるならば、毎回定期試験の準備として、
テキスト丸写ししただけ or ノー勉
で対策しているようなものです。

それでは、本番うまくいかないですよね（一部の天才は例外として。）

つまり、傾きが0ということはこのようなイメージ（全くもって異論を認めますので、ご自身の判断に任せます）

＝＝正しさを無視した例え話おわり＝＝

このReLU関数を用いれば、zが非負整数を取る限り常に導関数は1となりますから、すくなくとも勾配消失の問題を回避できるようになります。

畳み込みなどでこのReLUは威力を発揮しますが、その他でも十分に最近は活用されています。

・終わり

割と文章だけで活性化関数を扱ってみました。

とはいえ、数式の展開や変換などもありましたため、わかりにくかった部分も当然ながらあったかと思いますが、どうでしょうかw

これらの実装に関してはtensorflowや（tanhとかは）numpy, scipyで既に準備されているため、こちらがいちいち数式を手動で実装することはないですので、ご安心を。

では、また次回〜

・（不定期更新のおまけ）

珍しく文字数が少ないので、おまけを。

今回はos と pathlibを扱います。

個人で利用するときにこのos やら pathlibやらを扱うことなんてまずないとは思いますが、開発においてはほぼ必ず使うことになります。

とくにosモジュールは文字通りOSに関係して、

例えば、Macでpathを書くときは「/」で繋げますが、Windowsだと「¥」で繋げます。

例
Mac -> Users/taro/Desktop
Win -> Users¥taro¥Desktop

こうなると、例えば開発時に、「imgフォルダにある画像ファイルを繋げてpathを定義したい」ときに、ある開発者はWin環境で、ある開発者はMac環境で作業していれば、バグの嵐となりますw

それらを回避するためにこのosモジュールはとっっても大切です。

それだけじゃなくて、いちいち絶対パスを指定するために、長い文字列を定義したりすることも避けられます。

では、基礎から見て行きます。

まずはpathlibから。

コードをまずみましょう。

from pathlib import Path


reccurent_path = Path('./')

これ、何しているのかというと、今いるpathを定義しています。

Path()の中身は好きな存在しているpathであれば問題ないです。

from pathlib import Path


desktop_path = Path('/自身のpath/Desktop/')

次に、このreccurent_pathの中にあるiterdir()でpathを格納したiterator（厳密にはgenerator）を返します。

そう、iterater、めっちゃ出るんでるね。。

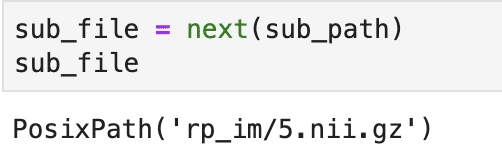
おさらいですが、iteratorはnext関数が使えるので、実際にnext関数でその要素を見てみましょう。

出力結果は人それぞれ違うと思いますが、要素が出てきたと思います。

では、この中にさらにアクセスしたい時は、path_iterを丸ごとlistに格納してその中の要素からさらにiterdir メソッドを使います。

そうすればこのsub_pathにあるファイル名とかフォルダをとってこれます。

ちょっと、おいおい、なにしてるの？ってなっているかもなので、図でみましょう。

って感じです（雑な説明ですみません。。）

では、これらを使ってosを使ってみます。

まず、ファイル名単体が欲しいときなどに使えるpathの分割から。

実際にpathが分割されました。

では、反対に指定したいpathとかを繋げたい時はjoin関数を使います。

最初に言ったように、Win, Macのpathの使い分けに依存せず自動的に繋げてくれるので、便利ですね（Djangoとかで割と使うイメージ）

ほんとはもっとosは使うのですが、一応ラスト。

python上でも一時的にフォルダを作りたいとき（一時的な格納の時にいちいちterminalではめんどいので。）はos.makedirs関数があります。

いま、new_folderというフォルダを同じ階層で作りたいとします。

この時、makedirs関数は既存のpathに同じフォルダが存在しているとエラーが出るので、path.exists関数でもしpathがあればTrueを返すことを利用して、存在しなければ作成というように工夫します。

実行するとnew_folderができていると思いますし、

上記のコードを2回実行しても特に何も変化ないと思います。

このos.path.joinはPathのインスタンスをそのまま使えたりするので、便利ですな。。

というわけで、これだけでマスターできるわけではないですが、実装段階では切っても切れないosモジュールの紹介でした！！