
クラスタリングを丁寧に。
前回まではクラスの分類の判定を行ってきました。
今回はクラスタリングを学んでいきます。
前回と違って、「正解がない状態で似たもの同士を分類していく」ことがテーマとなり、正解不正解の外を攻めていきます。
では、行ってみましょう。
・イントロ〜今回のテーマ
今回は教師なし学習を行なっていき、主にKMeansとDBCSAN、デンドログラムの可視化とかを行なっていきます。
基本的には複雑な数式は前々回のようなargmaxに比べればほとんどないはずです。(もしくは数学的に高度すぎるため割愛している)
これらは基本的な実装だけを行うのであれば、さらりと終わりますため、できるだけ丁寧にかつ適宜補足し(つまり自分が調べ)ながら書いて行けたらと思います。
・クラスタリングに出てくる用語たち
実装の前に少しだけ用語を。(これを読まないと理解できないってわけでもないので、飛ばしても流し見でもおけです。)
クラスタリングといえど、その種類は多岐に渡り、
階層ベース、グリッドベース、分散ベース、密度ベース、プロトタイプベースなどなど、、たくさんあります。
今回中心に扱うKMeansはプロトタイプベースのカテゴリのなかの一つで、いわゆるプロトタイプが各クラスタを表していることをプロトタイプベースと言います。
プロトタイプも細分化されていて、セントロイド(centroid)とメドイド(medoid)
の2種があります。。
セントロイドは名前に[center]とあるように類似する点の中心をプロトタイプとしてクラスタリングしていきます。
メドイドに関しては中心ではなく、何かしらの代表値を決めてその値に近い点を集めていくことになります。
kmeansはおもに円で囲めるような時に最適です(のちに後述)が、最初にkの値(いくつに分類すべきか?)を我々が決める必要があります。
しかし、データの次元数が大きければ当然可視化できないため、いきなり適切にkの値を決めることは難しいです。
これらの問題への対処なども後述していきますが、今回はまずは実装やおおまかな外観を掴むことを目的とするため、2次元データを中心に扱ってみます。
・データの準備
では、実装していきましょう。
ここで扱うデータはsklearnのなかにあるmake_blobsで散布したデータを作り上げてKMeansを利用していきます。
では、まずデータの準備から。
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150, n_features=2,
centers=3, cluster_std=0.5, random_state=0)
# sはサイズ
plt.scatter(X[:, 0], X[:, 1], c='white', marker='o', edgecolor='black', s=50)
plt.grid()
plt.tight_layout()
plt.show()
簡単にmake_blobsだけ補足しておきます。(公式ドキュメントではなく、 help関数で今回は見ました。)
help(make_blobs)make_blobs(n_samples=100, n_features=2, *, centers=None, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None, return_centers=False)
n_samples: 生成するサンプル数を指定します
n_features: 生成する特徴量の数を決めます。
centers: クラスターの数を設定します。
cluster_std: クラスタ内の標準偏差を指定
center_box: クラスタがランダムに生成された場合の各クラスタの中心となる座標(やや不明瞭)
return_centers:各クラスタの中心座標を出力するかどうか
shuffle, random_stateは割愛。
・KMeansのざっくりとした理論
実際にKMeansを使う前に少しだけ理論を説明します。
(コードだけみたい方は次の章に飛ばしてもそこまで支障はありません。)
KMeansは4つの手順で実行されています。
1. k個のセントロイド u_j (j=1~k) をランダムに選択
2. 各データ点を最も近いセントロイド u_j に割り当て
3. セントロイド u_j に割り当てられたデータ点の中心を計算しセントロイドを移動
4. データ点へのクラスタの割り当てが変化しない(収束している)、事前に設定したイテレーション回数に達するまで手順2. 3を繰り返す
実際には類似度はユークリッド距離(いわゆる純粋な距離という認識で大丈夫です)などが一般的に使われます。
このユークリッド距離を用いてクラスタ内誤差平方和(SSE: Sum of Squared Errors)は以下のように表せます。
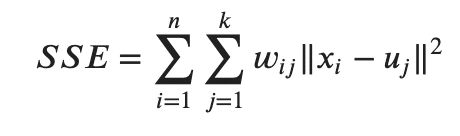
x_i はデータ点で、w_i_j はx_i がクラスタj に存在するときは1、ほかは0を返す関数です。
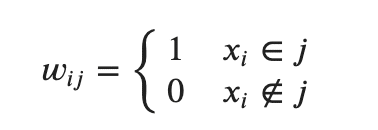
式としては以前に比べれば簡素ですね
・KMeansを実装
遠回りしてきましたが、実装にいきましょう。
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, init='random', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km.fit_predict(X)では、いつも通りドキュメントから。
class sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='deprecated', verbose=0, random_state=None, copy_x=True, n_jobs='deprecated', algorithm='auto')
n_clusters: クラスタの数
init: {‘k-means++’, ‘random’}で指定。クラスタの初期値の決め方を指定。
k-means++は後述
n_init: セントロイドを変更し、SSEが最小のモデルを採用する
max_iter: イテレーションの最大回数
tol: 収束と判定するためのtolerance(許容誤差)
precompute_distances: 将来的にこのパラメータは削除されるため割愛
copy_x: 距離を事前に計算する場合、メモリ内でデータを複製してから実行するかどうか
algorithm: Kmeansのアルゴリズムを指定。
他、省略。
今回のコードでは、クラスタを3つに指定。
n_initで10回セントロイドを移動させてSSEを評価し、最小のものを選択します。(10回とも重複はしません)
各実行時にイテレーション回数を制限することで計算コストを削減しています。また、その時に収束すると判定させる範囲をtolで指定しています。
max_iter or tol で収束の問題に対応しているため、計算が終わらないな〜って思った方はこちらの数値を見直してみましょう。
ちなみに、理論的にはk-meansは空のクラスタが発生することもあるのですが、sklearnはその問題は中で対処しているため、基本的に心配はありません。
・KMeansでクラスタリングしたものを可視化で確認
では、どのように分類されているのかみていきます。
その前に少し補足を。
cluster_centers_というKMeansの属性があり、各クラスタの中心座標を表します。
では、一気に可視化までいきます。
# クラスタ1
plt.scatter(X[y_km==0, 0], X[y_km==0, 1],
color='lightgreen', marker='s',
label='Cluster 1', edgecolor='black')
# クラスタ2
plt.scatter(X[y_km==1, 0], X[y_km==1, 1],
color='orange', marker='o',
label='Cluster 2', edgecolor='black')
# クラスタ3
plt.scatter(X[y_km==2, 0], X[y_km==2, 1],
color='lightblue', marker='v',
label='Cluster 3', edgecolor='black')
# 各クラスタの中心点
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
s=250, marker='*', c='red', edgecolor='black',
label='Centroids')
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
plt.show()
(プロットのコード説明は割愛します。)
今回はうまく分類できていますね!
最初にも書きましたが、実際は最初から可視化がむずしく、いきなりk(クラスタの数)を決めることはできないです。
この辺の対処などは後述していきます。
・k-means++でセントロイドの初期値を効率よく決める
先程、KMeansのパラメータにinitがあり、その中に'k-means++' という引数が存在していました。
デフォルトがk-means++であるように、基本的にはk-means++の方がよりスマートにセントロイドの初期値を決められることで知られています。
このk-means++に関してここでは解説していきます。
具体的な手順は以下となります。
1. データ点x_iからとりあえずランダムに1つだけ選択してそれをセントロイドとして設定。
2. このセントロイドと一番近いx_i(※)との距離D(x)を計算する
(※1で選択された点を除く)
3. 次のセントロイドu_pという点を選ぶのですが、さきほど選んだセントロイドと各データx_iの距離の総和を分母にし、分子は各x_iでの距離D(x_i)とした確率関数を元にセントロイドu_pを確率的に選択。
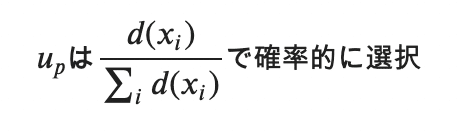
つまり、次に選ぶu_pはd(x_i)の距離が大きいものほど確率が大きくなるため、選ばれる確率が高くなるため、各セントロイドの距離が離れやすく、よりクラスタリングの精度が上がり役なるわけです。
4. これをk個選ばれるまで繰り返し、残りはk-meansの手続きを行う
実際にどう変わるのかをみてみます。
from sklearn.cluster import KMeans
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
km_1 = KMeans(n_clusters=3, init='random', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km_1.fit_predict(X)
# クラスタ1
ax1.scatter(X[y_km==0, 0], X[y_km==0, 1],
color='lightgreen', marker='s',
label='Cluster 1', edgecolor='black')
# クラスタ2
ax1.scatter(X[y_km==1, 0], X[y_km==1, 1],
color='orange', marker='o',
label='Cluster 2', edgecolor='black')
# クラスタ3
ax1.scatter(X[y_km==2, 0], X[y_km==2, 1],
color='lightblue', marker='v',
label='Cluster 3', edgecolor='black')
# 各クラスタの中心点
ax1.scatter(km_1.cluster_centers_[:, 0], km_1.cluster_centers_[:, 1],
s=250, marker='*', c='red', edgecolor='black',
label='Centroids')
ax1.legend(scatterpoints=1)
ax1.grid()
km = KMeans(n_clusters=3, n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km = km.fit_predict(X)
print(f'random \n{km_1.cluster_centers_} \n k-means++ \n{km.cluster_centers_}')
# クラスタ1
ax2.scatter(X[y_km==0, 0], X[y_km==0, 1],
color='lightgreen', marker='s',
label='Cluster 1', edgecolor='black')
# クラスタ2
ax2.scatter(X[y_km==1, 0], X[y_km==1, 1],
color='orange', marker='o',
label='Cluster 2', edgecolor='black')
# クラスタ3
ax2.scatter(X[y_km==2, 0], X[y_km==2, 1],
color='lightblue', marker='v',
label='Cluster 3', edgecolor='black')
# 各クラスタの中心点
ax2.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
s=250, marker='*', c='red', edgecolor='black',
label='Centroids')
ax2.legend(scatterpoints=1)
ax2.grid()
plt.tight_layout()
plt.show()
実際にセントロイドの座標が違うことを確認できましたね!
・ハードクラスタリング・ソフトクラスタリング
クラスタリングのアルゴリズムには種類がありまして、k-meansのような単一クラスタにデータ点が属するような場合はハードクラスタリング、複数クラスタに属する場合をソフトクラスタリングと言います。
ソフトクラスタリングはfuzzy clustering(ファジークラスタリング fuzzy: ぼやけた)とも言われ、Fuzzy Cmeans(FCM)が代表的です。
ここでは、簡単に理論の説明を行うにとどめるため、先に進みたい方はスキップしてください
ちなみに、コーディングしてみたい方は
https://pythonhosted.org/scikit-fuzzy/auto_examples/plot_cmeans.html
が参考になります
クラスタ数k=3 のとき、xがu_j(j = 1, 2, 3)に含まれる確率で表解されることがソフトクラスタリングの特徴です。
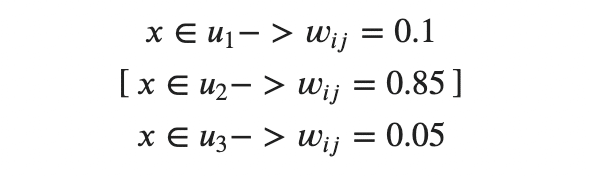
基本的な操作はk-meansと同様であり、目的関数JmはSSEと似ています。
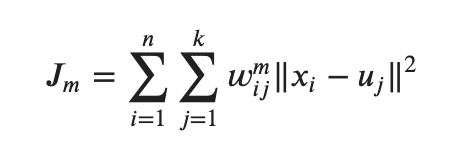
SSEとちがい、重みw_i_j(今回の場合、0, 1を取るのではなく、クラスタの所属確率が割り振られている点に注意) に指数mが付けられていることがポイントです。
このmはファジー性(あいまい性)を制御するファジー係数と言われ、mが大きいほどw_i_jが小さくなります。
ちなみに、このw_i_j は次のような手順で作成されています。
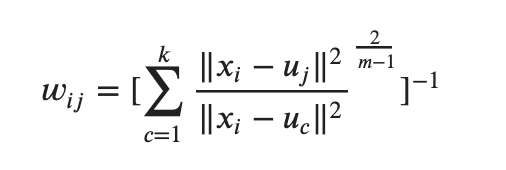
うげぇ〜〜ってなりそうかもしれませんねw
クラスタ自体の中心u_jに関しては クラスタ内のデータ点の平均で算出できます。
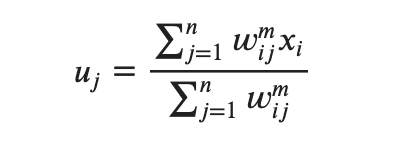
FCMの方がイテレーションの回数が少ないことで知られていますが、計算コストはk-meansの方が良いとされています。
この辺に関しては手計算するわけでもないので、さらっと流すことに止めます。
・エルボー法で適切なkを確認する
k-meansにおいて、どの程度のkが適したクラスタリングになるのかに関しては徐々に数値を変更しなければなりません。
ここでdistortion(歪み)という数値を元に確認することで、ある数値 k において急速に歪みが減る点kを用いて効率よくクラスタリングの数を見つけることができます。
これをエルボー法と言います。
コード自体は優しいのでサラッとみてみましょう!
distortions = []
for i in range(1, 11):
km = KMeans(n_clusters=i, n_init=10, max_iter=300, random_state=0)
km.fit(X)
# inertia_で歪みを数値的に表示
distortions.append(km.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()
k=3で急速に下がっていることが確認できます。
つまり、今回はk=3が適していたといえますね!
ちなみに、なぜに「elbow(ひじ)」なのかと言いますと、急速に曲がっている部分がひじっぽいことから来たそうです。
・クラスタリングの性能を数値化して確認する(シルエット図)
シルエット分析というkmeansだけでなく、クラスタリング全般に使える評価指標の一つをここでは取り扱います。
クラスタ内にどのくらいデータが密になっているのかを図ることで、適したクラスタリングがされているのかがわかります。
(当然ながら良いクラスタリングであればデータ点がめちゃくちゃ密になってるわけで、このご時世だと政府から苦情が来るレベルになるわけです。)
シルエット図に関して必要なシルエット係数というのがあるので、簡単に解説してから可視化にいきましょう。
---- 余談 -----
ちなみに、もちろんコードを書いていくのですが、この可視化のプロットする部分の関数が非常にめんどいす。(一度書いてしまえばテンプレである程度使えるはずですが、まぁ、めんどいす。。)
---- 余談おわり -----
シルエット係数を計算するにあたり、凝集度と乖離度というものをまず求めます。

凝集度はある点xi が属するクラスタの全データとxiの距離の平均を求めます。
乖離度はある点xiに一番近い(属しているクラスタ以外の)クラスタの全データの平均距離を算出します。
凝集度をa, 乖離度をbとして、この差分(b - a)をa, bの大きい方で割ったものがシルエット係数となります。
silhouette = (b - a) / max(a, b)
このシルエット係数のとりうる範囲は-1 ~ 1で、1に近づくほど理想的なクラスタリングといえ、-1に行くと改善の余地ありとなります。
いつもながらですが、これらの係数は関数ですでに用意されているため、計算する必要もないです。
では、コードに行ってみましょう!
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_samples
from matplotlib import cm
km = KMeans(n_clusters=3, n_init=10, max_iter=300, random_state=0)
y_km = km.fit_predict(X)
cluster_labels = np.unique(y_km)
print(f'cluster_labels.shape: {cluster_labels.shape}')
n_clusters = cluster_labels.shape[0]
# シルエット係数を計算
silhoutte_vals = silhouette_samples(X, y_km, metric='euclidean')
print(f'silhoutte_vals[:10]: \n{silhoutte_vals[:10]}')
# プロットの準備
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
# 各クラスラベルの係数のみを取り出す
c_silhoutte_vals = silhoutte_vals[y_km==c]
c_silhoutte_vals.sort()
# 描画の上端の値を設定
y_ax_upper += len(c_silhoutte_vals)
# 描画時の色の値をセット
color = cm.jet(float(i) / n_clusters)
print(f'cm.jet: \n{cm.jet(float(i) / n_clusters)}')
plt.barh(range(y_ax_lower, y_ax_upper),
c_silhoutte_vals,
height=1.0,
edgecolor='none',
color=color)
# クラスタのラベル位置を指定
yticks.append((y_ax_lower + y_ax_upper) / 2.)
# 次の描画のスタート位置
y_ax_lower += len(c_silhoutte_vals)
silhoutte_avg = np.mean(silhoutte_vals)
plt.axvline(silhoutte_avg, color='red', linestyle='--')
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhoutte coefficient')
plt.tight_layout()
plt.show()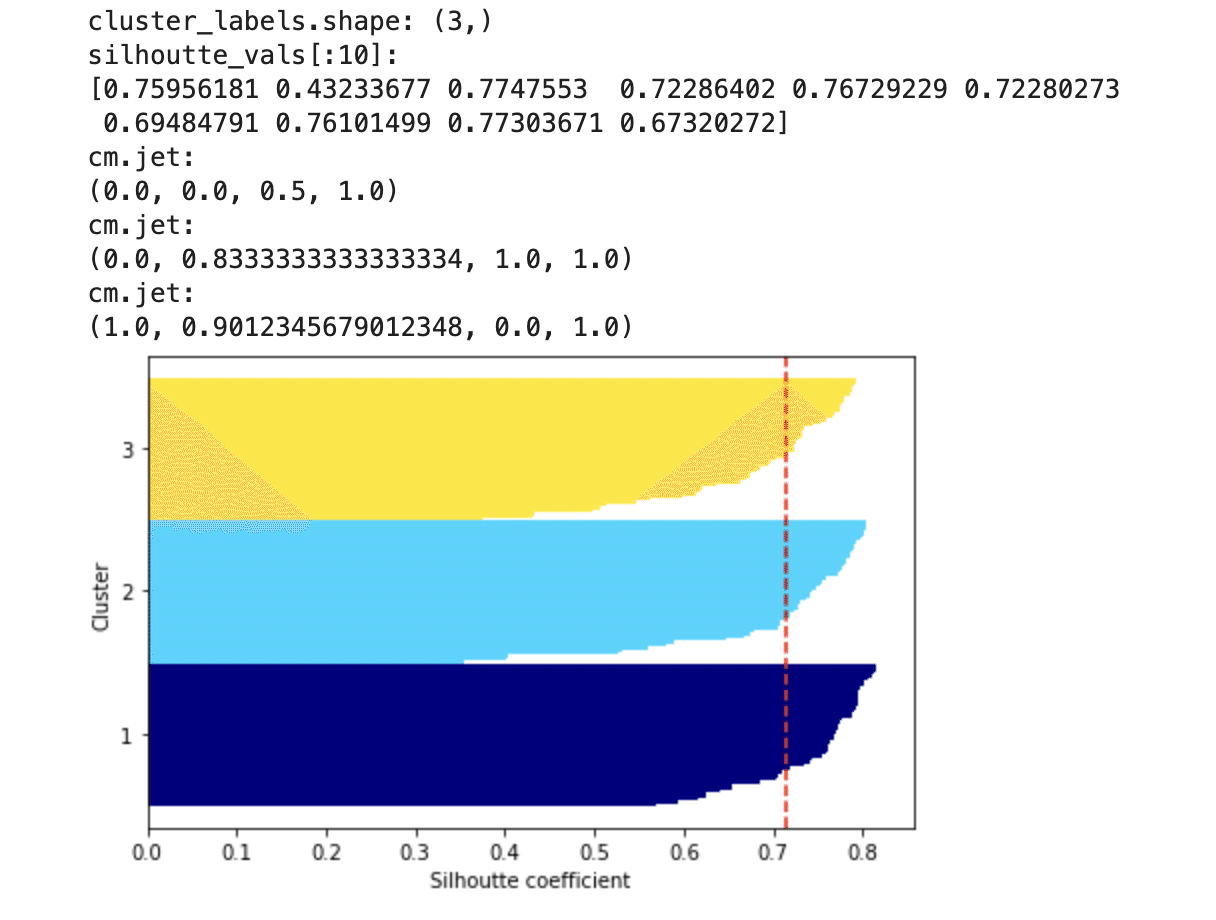
(参考テキストのコード、ダサいな〜なんて思いながら書いたのですが、)色々みていきましょうwwww
まずはsilhouette_samplesから。公式ドキュメント
sklearn.metrics.silhouette_samples(X, labels, *, metric='euclidean', **kwds)
X: サンプルデータ
labels: 対象となるクラスタのラベルを格納しているデータ
metric: 各データと測定するデータの距離の測り方(str もしくは関数でも指定可能)
返り値はprintを一応しておりますが、各データにおいて算出したシルエット係数が格納されています。
あとはプロットのためのいろんな準備なのですが、plt.barhってなに?ってなったので解説しておきます。
そもそもhorizontal barのことをbarhと言いまして、水平方向の棒グラフと思ってもらっておけです。
matplotlib.pyplot.barh(y, width, height=0.8, left=None, *, align='center', **kwargs)
つまり、基本的にy軸視点で考えます。
y: 棒グラフのy座標を指定(いわゆる座標点を設定し、±height/2だけ上下に広がるイメージ)
width: 棒の幅を指定。今y軸は(y_lower, ..., y_upper)の範囲で指定されて、その幅(いわゆるx軸の座標という感覚)
height: yで指定した座標から上下に指定した数値の半分づつ広がる
ちょっと、簡単なコードで例をみてみます。
import matplotlib.pyplot as plt
plt.barh([0, 1], [-1, 0.5], height=1)
plt.show()
y=[0, 1]なので、まずy=0と1が設定されています。
次に、width=[-1, 0.5]なので、x=-1と0.5に点が打たれます。そしてそれぞれ長さ1, 0.5の棒グラフが引かれることになります。
この時点で(x, y) = (-1, 0), (0.5, 1)にプロットが打たれているというイメージ
そこでheight=1としたので, y=0から±0.5だけ広がり、さらにwidth=1分だけ広がっています。
これを指定しているyの数値だけ広がります。
----------------
今回の例を見ると、y=range(y_lower, y_upper)の範囲で最初は0~(クラスタ1のデータ点の数)までの整数値がy座標に設定されています。
そこで、それぞれのwidthは昇順にsortされたsilhoutte係数の分だけ横に広がります(なんか上に行くほど長くなっているのはsortしているため)
そして、それぞれの幅を1に設定して完成というわけです。
ちなみに、こんかいはk=3である程度良いのですが、実際k=2の時(k=3よりも悪いクラスタリング)ではシルエット図がどうなるのかだけみて今回は終わろうと思います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_samples
from matplotlib import cm
# k=2で試す
km = KMeans(n_clusters=2, n_init=10, max_iter=300, random_state=0)
y_km = km.fit_predict(X)
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
# シルエット係数を計算
silhoutte_vals = silhouette_samples(X, y_km, metric='euclidean')
# プロットの準備
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
# 各クラスラベルの係数のみを取り出す
c_silhoutte_vals = silhoutte_vals[y_km==c]
c_silhoutte_vals.sort()
# 描画の上端の値を設定
y_ax_upper += len(c_silhoutte_vals)
# 描画時の色の値をセット
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper),
c_silhoutte_vals,
height=1.0,
edgecolor='none',
color=color)
# クラスタのラベル位置を指定
yticks.append((y_ax_lower + y_ax_upper) / 2.)
# 次の描画のスタート位置
y_ax_lower += len(c_silhoutte_vals)
silhoutte_avg = np.mean(silhoutte_vals)
plt.axvline(silhoutte_avg, color='red', linestyle='--')
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhoutte coefficient')
plt.tight_layout()
plt.show()
これを見るとシルエット係数が1から遠くなり、先程の方がやはり優れていることがわかりました。
・(おまけ)こんなプロット毎回書いてられんよ!って方に
毎度plt.barhでsilhoutteのsortを考慮したりなんてわかんないよ!って方に、一瞬で可視化できるパッケージがあるので、簡単に紹介だけ。。
コードからどうぞ
from yellowbrick.cluster import SilhouetteVisualizer
km = KMeans(n_clusters=3, n_init=10, max_iter=300, random_state=0)
visualizer = SilhouetteVisualizer(km)
visualizer.fit(X)
visualizer.show()
yellowbrickという機械学習の可視化に強いモジュールがありまして、その中のvizualizerを使えば簡単に可視化できます
公式ドキュメント
scikit-yb.org/en/latest/api/cluster/silhouette.html
内容の説明は割愛しますが、なんかplotしたくない!って方には頭の片隅に入れておくと便利かもですねぃ!
・一旦終わり
一旦区切ります。
次回はクラスタリングの続きでデンドログラムやDBSCAN(多分いけると思いますが、もしかしたらデンドロで終わるかも、、)で階層クラスタリングを攻めていきます。
ってなわけでまた次回
