
tensorflowを基礎の基礎から (自然言語処理 番外編Ⅰ)
今回からtensorflow基礎をスタートし、準備ができたところでRNNのLSTMや実装を再開しようと思います。
前回のRNNでもSimpleRNNには触れたのですが、やはりtensorflowの理解なしでは限界があると(私が)感じたので、tensorflowをこの機に学んじゃえ!って感じで書いて行きます
tensorflowの良質な動画・記事なんてありふれてますので、いつもながらそれぞれが好きな方法で学んでいただければと思います。
では、今回もよろしくお願いいたします。
・テンソルとは?〜イントロのイントロ〜
tensorflowはgoogleが作った〜でとかというイントロは今時点ではここで書く理由もないので、早速。
tensorflowとかいってますけど、そもそもとしてtensor(テンソル)の理解は多少必要かなと思います。
大抵の学習では、せいぜい行列を扱うことが一般的ですが、数学的に多次元を扱うとなれば「テンソル」が必要となります。
このテンソルとは、簡単にいえば「全て」を表すのですが、わかりやすく言えば行列の一つ上の階層です。
・・・
多分、これだけでは何いっているかわからないと思うので、順を追ってみて行きます。
まず、数学として最初に考えるscolar(スカラー)は「点」を示します。
これを階層0のテンソルと言います。
次に、点と点を繋げると一本の直線(ここではベクトル)となります
これを階層1のテンソルと言います。
次に、ベクトル同士を広げていくと一つの平面(ここでは行列)となります。
これを階層2のテンソルと言います。
そして、さらに行列同士を繋げると空間となります。
これは階層3。
さらに、これらをどんどん増やすことでテンソルの階層は上がって行きます。
厳密性を一切排除したテンソルの説明はこんな感じです。
・・・・
これのなにがどう良いものか?なぜに急にテンソル?っていう疑問が
(私は)あるので、ここからもう少し突っ込んでみましょう。
なんで私のような一般人はテンソルという言葉に馴染みがないのか、ですが、調べるとテンソルは物理学でよく出てくるそうです。
自分は行列を重ね合わせてるもんしょ!くらいの認識だったのですが、このnoteを書くにあたり、ちゃんと調べてみました。
実はテンソルといえど、数学や物理などで定義が変わるため、結構調べた結果、「よーわからんw」ってのが本音です
「がっつりテンソルを数式で理解しなければいけない状況」もすぐにはないので、なんかよくわかんないよ!って方も気にしなくて構いません。
基礎のコードだけ練習したいって方は、全然読み飛ばしてくださいw
一応、今回説明するのは「自分が理解しやすかった『テンソルの定義』」に基づいて説明するため、正確性の観点はちょっと怪しいですw
ちゃんと定義しようと思えばテンソル積、内積、写像、その他数学の証明などが必要となり、無謀と感じましたw
・脱線〜ベクトル・行列のちょっと深掘り〜
脱線しますので、興味ない方は読み飛ばしましょう。
ちょっとだけベクトルについて。
まず我々が高校数学で学ぶベクトルは「矢印」っていう印象が強いと思いますが、大学に行けば「ある性質をもつ空間の元(げん。いわゆる集合の要素)」をベクトルと言います。(これ以上は踏み込みませんw)
機械学習の話をすれば、pandasのDataFrameには.valuesという属性があり、numpy.array形式に変換してくれるものがありました。
つまり、一行一行を「ベクトル」としてみているわけで、いわば「一つの個体が持つ情報」を表現しているとみなせるわけです
では、次に行列ってなんでしょうか??
今まで配列や行列を気にせず実装とかしてきたわけですが、行列とは
あるベクトルの向きや大きさを変えるための装置
みたいなものです。
ちょっと例を見てみましょう。
まず、シンプルにx軸方向にある単位ベクトル(1, 0)を用意して、
行列[[0, 1], [1, 0]](表記上見にくいですが、2行2列で第一要素が0・・)を考えてみましょう。

図の中に式まで書きましたが、この行列によって、向きは90°移動しています。
同様にいろんな例を出せますが、RNNの回のGRUらへんで
「情報があちこち飛んでしまっている」
という表現をしたかと思いますが、これは上記のことを表現したに過ぎません。
つまり、言語(実際には数値)のベクトルがW_xhなどによりそれが持つ情報が更新されて、他のものと結合しちゃうから記憶が保持しにくいって感じです。(すっきりしました??)
・(脱線3)〜物理のテンソルの説明〜
説明を再開します。
かなりのサイトを見てみましたが、一番わかりやすかった説明は
物理量で見ていくこと
だったので、それをなるべく平易な言葉を用いて利用して行きます。
(たぶん)物理嫌いの人でも視覚的に理解できるようにしているはずです(つもり)。
ちなみに、数学的に言えば、「テンソル空間の元」みたいな「なんですかそれ?」ってなります。。
では、行きましょう。
・物理でのテンソルの説明開始
そもそも我々が生きている空間は
スカラー(scolar)とベクトル(1st order tensor)で説明することができます。
具体的にscalarの例としては、重力g, 速度v, 時間t みたいな「一つの物理量」で表現がされます。
次にvectorは、位置ベクトルとして、座標a = (0, 1, 3){= (x, y, z)} とか、
速度ベクトルu = (u, v, w) = (3, 2, 7) みたいに、一つの変数の中に3つの要素を格納できます(語弊を招く表現をあえてしますが、いわゆる3次元空間はベクトルで表現できる、みたいな。)
では、tensorは「9つの物理量」を持つものになります
ーー(補足)ーー
(ちなみに、scalar = 3**0=1, vector=3**1=3, tensor=3**2=9となり、それぞれを1st order tensor, 2nd order~,...みたいに表現されるそうです。)
ーーーーーーーー
ちょっとここら辺で図を見ながら補足して行きます。
まず、vectorから。

物理なので、3次元空間で考えると、vectorの表現は上記のようになります。
・・・ま、そうですよね、くらいだと思います。
では、テンソル。
テンソルのは線ではなく、小さな箱を空間におき、力を加える向きを考えることで表現できます。
一つの例を出します。

(図が寄りすぎ。。)
ここで考えるべき項目は2点。
・力が作用している面(ここではxy平面)に垂直な軸(軸)
・引っ張られている方向の軸(ここではy軸。ちなみに矢印の向きが逆でもおけ)
これらを考えます

この情報をτ_zy(τは「たう」)として表現します。
そうすると、それぞれの面3つに対して3軸の力の方向性が考えられるため、3×3 = 9つの物理量が出てくることがわかります。

まとめると以下。

これらを用いて上記の体積に働く力を求めたりします。
・・・
な〜んか思ってたのと違う印象が(私には)ありますが、
つまり、一つの記号に9つの物理量を持ったのがtensor(厳密には応力テンソル?)となります。
・テンソルは結局?
さきほどのtensorとtensorflowで扱うテンソルはちょっと差異がありまして、現実的に利用する場合は、
やはり
行列が組み合わさったもの(サイトとかでもよく見るやつ)と考えたり、情報がいーーっぱいあるもの
くらいの認識で進めた方が、よほどいいと思ったのが調べてみた感想です。(ながながと物理でのテンソルを書き散らしてしまった。。)
そんなわけで、テンソルをガチ理解しようとすると数学の参考書を片手に置いておく必要が出てきますので、さっさと文法に行きます
・tensorflow基礎文法~イントロ~
まずは本当の算術の文法から、kerasとかのお作法や実装などを進めて行きます。
array形式と相性がいいので numpy と似ているものの、癖があったりしますので、ゆっくりと。
ちなみに、公式のチュートリアルはこちら。
・tensorflow基礎~Tensor型に触れる~
まずはインストールから。
今回もローカルではなく、colab使います。
tensorflowはpip install で気軽に使えますし、tensorflow-gpuもこれで行けます
!pip install tensorflow
!pip install tensorflow-gpu
!pip install tensorflow-datasetsでは、行きます。
まずはいままで不自由なく使ってきたarrayやlistをテンソルにしてみます。
まずはコードから。
import tensorflow as tf
import numpy as np
np.set_printoptions(precision=3)
a = np.array([4, 5, 6], dtype=np.int32)
b = [9, 10, 11]
t_a = tf.convert_to_tensor(a)
t_b = tf.convert_to_tensor(b)
print(a)
print(type(a))
print(t_a)
print(type(t_a))
print(t_b)
convert_to_tensorでargumentにあるvalueをTensor形式にする関数です。
printで色々出してみましたが、tensor形式にすることにより、全く別物となっている点に注意が必要です。
numpy形式のものが同じ配列や情報であったとしても、tensor形式になっています。
では、ここでnumpyとtensorflowの演算をしてみるとどうなるかみて行きましょう。
n_ones = np.ones((2, 3))
print(n_ones)
print(n_ones.shape)
print('-'*10)
t_ones = tf.ones((2, 3))
print(t_ones)
print(t_ones.shape)
print('-'*10)
print(n_ones + t_ones)
print(n_ones + t_ones.numpy())
同じshapeを持ちますが、無理くりたすと、tf.Tensorとなり、テンソル形式に吸収されていますね・・(公式チュートリアルでも説明されていました。)
しかし、numpyでの演算をしようとするとnumpy に変換されたり、.numpy()で明示的な変換もできます。
print(type(np.add(t_ones, 32)))
print(np.add(t_ones, 32))
定数値からtensor にするのはconstant関数を用います。
const_tensor = tf.constant([1.2, 5, np.pi], dtype=np.float32)
const_tensor![]()
ちなみに、先程のbはすでにあるものをtensorにしたいときに使いますが、constantで同じ数値と型を指定すれば同じものになります。
b_constant = tf.constant([9, 10, 11], dtype=np.int32)
print(b_constant == b)![]()
(条件式使うと、なんとbooleanのTensorが出てきました。。知らなかった。)
・tensorflow基礎~形状の操作~
引き続き基礎を見て行きます。
細やかな説明をすることもないので、適宜必要な部分だけ補足する程度でちょっとサクサク行きます。
まずはpandasのastypeのように型変換をするcast関数を見ていきましょう
t_a_new = tf.cast(t_a, tf.int64)
print(t_a.dtype)
print(t_a_new.dtype)
tensorの次元追加(変更)、転置なども見て行きます
- 転置
t = tf.random.uniform(shape=(3, 5))
t_tr = tf.transpose(t)
print(f'{t.shape} --> {t_tr.shape}')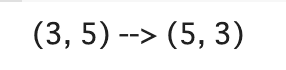
- 形状変更
t = tf.zeros((30))
t_reshape = tf.reshape(t, shape=(5, 6))
print(f'{t.shape} --> {t_reshape.shape}')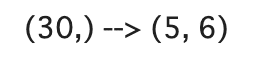
- 次元削除
t = tf.zeros((1, 2, 1, 4, 1))
print(t)
t_sqz = tf.squeeze(t, axis=(2, 4))
print(f'{t.shape} --> {t_sqz.shape}')
このsqueezeは少し補足します。
size = 1の次元を削除するのがsqueezeですが、パラメータaxisを設定しない場合は次元がsize=1のものすべて削除します。今回axis=(2, 4)としているため、size=1の2番目と4番目の要素を削除します。
ちょっと、t = tf.zeros((1, 2, 1, 4, 1))を見慣れないと思うので、どうやってみるのか確認しておきます。

左から順番に1 -> 2 -> 1 ・・・と要素が格納されていますね!
これの中で要素が1 つ(1次元)のものを取り除くのがsqueezeとなります。
t_sqz
実際に(1, 2, 4)の順番で要素が格納されたTensorに変換されていることがわかりました!
ここら辺を常に意識することは、ほぼない(人間がそもそも考えにくい次元数w)ですが、一応補足でした。
・tensorflow基礎~演算いろいろ~
では、いわゆる算術演算を見て行きます。
まず、[-1, 1]に一様に分布する範囲からランダムに要素を取り出したものと、標準正規分布に従うランダムな要素を用意して始めます。
tf.random.set_seed(1)
t1 = tf.random.uniform(shape=(5, 2), minval=-1.0, maxval=1.0)
t2 = tf.random.normal(shape=(5, 2), mean=0.0, stddev=1.0)
print(t1)
print(t2)
- 乗算
t3 = tf.multiply(t1, t2)
t3
注意として、いわゆる行列の掛け算ではなく、対応する要素同士の掛け算(アダマール積)です。
なので、shapeのちがうTensorではErrorが出ます。
_t2 = tf.random.normal(shape=(4, 2), mean=0.0, stddev=1.0)
_t3 = tf.multiply(t1, _t2)
_t3
- 平均や標準偏差
t4 = tf.math.reduce_mean(t1, axis=0)
t4![]()
※標準偏差はreduce_stdでおけ
(自分もいまだにaxisの参照方向がピンとこない時があるのですが、迷ったら以下のURLを参考にしたり、その場に流されてみることをお勧めしますw)
なぜ「reduce」っていう言葉がついてるのか気になったのですが、公式のチュートリアル曰く、inputのTensorの次元数を減らして平均を算出しているからっぽいです。
- 行列の積
_t5 = tf.linalg.matmul(t1, tf.transpose(t2))
t5 = tf.linalg.matmul(t1, t2, transpose_b=True)
t6 = tf.linalg.matmul(t1, t2, transpose_a=True)
print(_t5)
print(t5)
print(t6)
行列の積をする場合は、linalgの中にあるmatmul (matrix multiply)でできますし、パラメータにはtranspose_a(b)もあるため、わざわざtf.transposeをしなくてもパラメータを設定するだけで転置してくれます。
どちらを転置するかによってもちろん出力される行列のshapeも変更されるのはnumpyでもお馴染みですかね?
- normの計算
norm_numpy_L1 = np.linalg.norm(t1.numpy(), ord=1, axis=1)
norm_numpy_L2 = np.linalg.norm(t1.numpy(), ord=2, axis=1)
norm_t1_L1 = tf.linalg.norm(t1, ord=1, axis=1).numpy()
norm_t1_L2 = tf.linalg.norm(t1, ord=2, axis=1).numpy()
print('L1の比較')
print(norm_numpy_L1)
print(norm_t1_L1)
print('-'*10)
print('L2の比較')
print(norm_numpy_L2)
print(norm_t1_L2)
実際にnumpyと遜色なくTensorでも計算できていますね!
・tensorflow基礎~Tensor形式で分割や連結~
- 分割
arrayやDataFrameのようにTensor形式を分割や結合する時はsplit()関数が使えます。
t = tf.random.uniform((6, ))
print(t.numpy())
t_splits = tf.split(t, num_or_size_splits=3)
print(type(t_splits))
[t_split.numpy() for t_split in t_splits]
t = tf.random.uniform((5, ))
print(t)
t_splits = tf.split(t, num_or_size_splits=[2, 3])
print([t_split.numpy() for t_split in t_splits])
t = tf.random.uniform((6, ))
print(t)
t_splits = tf.split(t, num_or_size_splits=[1, 5])
[t_split.numpy() for t_split in t_splits]
ちょっとだけ意識しておきたいのはsplit関数で出力されるのは「list形式」であることです。
今まではすべてTensor形式で出力されていましたが、分割により出力されるのはlistのため、リスト内包表記などが使えます。
- 連結
numpyのvstackやhstackのように積み上げや連結する時はstackやconcat関数を用いることができます。
-- concat
A = tf.ones((3, ))
B = tf.zeros((2, ))
C = tf.concat([A, B], axis=0)
print(C)![]()
-- stack
A = tf.ones((3, ))
B = tf.zeros((3, ))
S = tf.stack([A, B], axis=1)
print(S)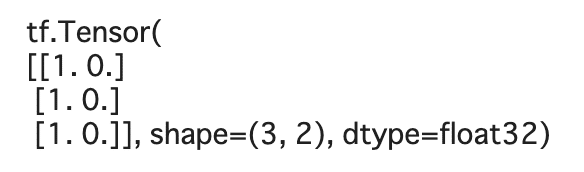
同サイズのものであれば。積み上げることで2次元にできます。
・tensorflowでデータの取り扱い・処理
大体の基礎の基礎は終わりました。
ここからはデータセットの取扱い方を見て行きます。tensorflowを使う時点でかなり膨大なデータを扱い、そしてブラックボックスと言われているほど高度な処理をDeep Learningで行うことが想定されます。
sklearnでも学びましたが、そこで都度前処理をするのではなくtensorflowにもパイプラインを構築して前処理などの一連の作業を簡単に行うようなクラスが組み込まれています。
ここではtensorflowでのデータセットの扱い方の基礎を見て行きながら理解を深めていこうと思います。
(いつもながら文字数が膨大になってきたので、kerasは次回に回します。。)
まずは既存のデータをTensor型に変更していく作業のfrom_tensor_slicesを確認しましょう。
a = [1.2, 3.4, 7.5, 4.1, 5.0, 1.0]
ds = tf.data.Dataset.from_tensor_slices(a)
print(type(ds))
print(ds)
実際にtypeもtensorflowの特殊なclassに変更されています。
要素の取り出し方は通常のリストのように取り出せます。
[item for item in ds]
要素だけ欲しい時はas_numpy_iteratorを使うとできます。
[item for item in ds.as_numpy_iterator()]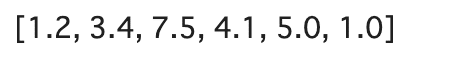
ちょっとだけtensorflow.data.Datasetの他の関数も見ておきます。
from_tensor_slicesのようにlist形式のデータを一つずつ取り出したりもできますし、
TextLineDatasetで.txt形式のファイルの読み込み、
list_files([path1, path2, ...](or './*.txt'のような形式))でファイル名の取得ができたりします。
! echo 'Hello Tensorflow!' > test1.txttextfile = tf.data.Dataset.list_files('./test1.txt')
list(textfile.as_numpy_iterator())
- バッチサイズを指定してバッチの作成
バッチ(データの中から適当にデータを取り出してミニデータにしたもの)を作成するときは.batch(n)で指定します。
print([item.numpy() for item in ds])
ds_batch = ds.batch(3)
for i, elem in enumerate(ds_batch):
print(f'{i}: {elem.numpy()}')
ds_batch = ds.batch(2)
for i, elem in enumerate(ds_batch):
print(f'{i}: {elem.numpy()}')
print('-'*10)
ds_batch = ds.batch(4, drop_remainder=True)
for i, elem in enumerate(ds_batch):
print(f'drop reminder True {i}: {elem.numpy()}')
drop_remiderにより、dataset.batch(batch_size=n)にてdatasetの要素数がbatch_sizeで均等に割れない時あまりの分を消すことができます。
・一旦区切り
区切りがいいわけでもなんでもないのですが、文字量的に一旦区切りますw
(というか、最初の物理のtensorの説明消せばいいのにって感じですが、なんかせっかくやったのにというサンクコストが大きくてですね、、のこしましたw)
次回も引き続きtensorflow基礎をします。
徐々に徐々に(私が)tensorflowの扱いに慣れていければと思いながら書いて行きます。
とはいえ、これらをサラサラと書けるようになるのはもちろんベストですが、まずはtensorflowの扱いや雰囲気を身につけていく感じでいいと思います。
ある程度の基礎が終わればRNNのLSTMなどに再開します。
では、また次回
