
Tableau なめらかな曲線で繋ぐ(Sigmoid関数)
グラフは棒や線など直線的なものが多いですが、たまには線がイイ感じで曲がってほしい時もあります。今回はサンキーダイアグラムでもよく利用される Sigmoid関数 を私なりに勉強してみましたのでご紹介します!
なお、曲線を描くために多くはリレーションなどでプロット用のデータを別途用意しますが、今回は既存のデータのみで曲線を描きますので、抽出したデータソースなどでもご利用いただけます。

■Sigmoid曲線とは
なめらかな曲線を描くためにSigmoid関数を利用します。Tableauでは線を引きたい場所をプロットし、マークを線にして曲線を描くことになります。
縦軸が 0 ~ 1 の値、横軸は -6 ~ +6 の値をとります。そして横軸が プラス方向に進むにつれ、縦軸の値が大きくなり、横軸が両端に近いほど縦軸の値の変動が小さくなります。またプロットした点の数が多いほど曲線がなめらかになります。

■Sigmoid曲線を描くために
・枝分けするディメンションの作成
まず最初に枝分けしたいディメンションを決めておきます。せっかくなのでパラメータでいくつか選択できるようにしてみます。今回は「サンプル スーパーストア」のデータを利用しているため、以下のようにしました。
ディメンションの選択:パラメータ
0.選択されたディメンション:パラメータの値で変化する計算フィールド

・プロットするデータを作る
曲線を描くために点を配置する必要がありますので、今回は計算フィールドで仮想的に作ります。なお点の数が多いほど曲線がなめらかになりますが、点の数を任意に変更できるようにパラメータで作成します。
今回は初期値を 20 にしておきます。
点の数:パラメータ

そして点をプロットするために以下の計算フィールドを作成します。
1.パス:プロットするデータを作る計算フィールド

計算フィールド名: 1.パス
IF [0.選択されたディメンション] == { MIN([0.選択されたディメンション]) }
THEN TODAY()
ELSE TODAY() + [点の数] - 1
END作成した計算フィールド「1.パス」を不連続で配置して確認してみます。

{ MIN([0.選択されたディメンション]) } が「家具」のため、「家具」にはTODAY()の 2023/07/17、それ以外は TODAY + 20(点の数) -1 で 19日プラスになった 2023/08/05 が入ります。
そして「1.パス」で「欠落した値を表示」にチェックを入れると、「点の数」で指定した20個の点が横方向にプロットされます。
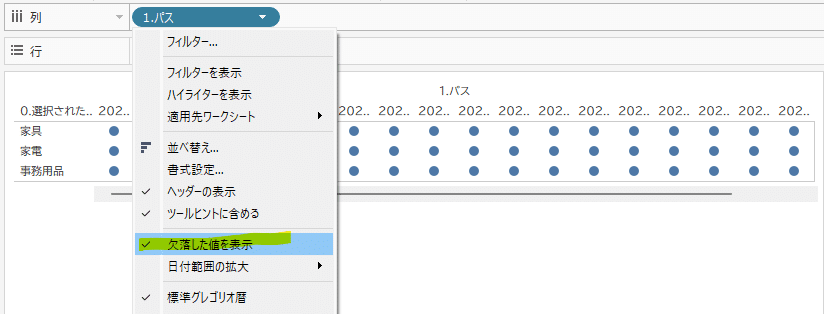
「欠落した値を表示」を有効にすることで、1日毎に仮想のデータが作られたことになります。例えば色に「1.パス」を入れると、本来データや計算上に無いはずの日まで色が付きます。

そして INDEX() を置いてみると TODAY() の 1 起点として 20 まで表示されました。パラメータで作った「点の数」を変えることで、表示される値の個数も変わります。これでプロットするデータの作成は完了です。

・横軸の値を計算する
Sigmoid関数の横軸は -6 ~ +6 の値をとるため、点の位置を -6 ~ +6 の間で均等になるように計算フィールドを作ります。

2. T:点を -6 ~ +6 の間で均等になるようにする計算フィールド

計算フィールド名: 2.T
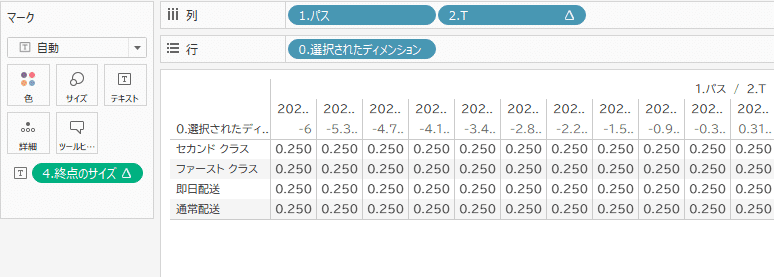
((INDEX() - 1) / ([点の数] - 1) ) * 12 - 6計算内の INDEX() は 「1.パス」に沿って計算する必要があるため、計算フィールドの「既定の表計算」で「1.パス」を指定しておきます。これで -6 ~ +6 の間で点の位置が均等に計算されるようになりました。

・Sigmoid曲線を描く
いよいよSigmoid曲線を描きます。曲線を描くためには以下の計算フィールドを作ります。
3.Sigmoid:Sigmoid曲線を描くための計算フィールド

計算フィールド名: 3.Sigmoid
1 / (1 + EXP(1)^ - [2.T])そしてこれまで作成した3つの計算フィールドを配置します。
まず、「1.パス」を 行 または 列 に配置し、「欠落した値を表示」にチェックを入れた後、詳細にドラッグします。

次に列に「2.T」、行に「3.Sigmoid」を配置すると、S字にプロットされたグラフが出来上がります。これでSigmoid曲線は完成です。

パラメータの「点の数」を変えることでプロットされる点も変動します。

■ディメンション数に応じて曲線を描く
・始点と終点について
Sigmoid関数 では始点と終点の位置を決めることで、なめらかな曲線を描いてくれます。そしてそれぞれは 0 ~ 1 の間の値になります。以下のように「始点」と「始点」を複製した「終点」のパラメータを作ってみます。

そして検証用で以下の計算フィールド「99.線」を作ります。

作成した計算フィールド「99.線」を配置してパラメータの「始点」「終点」の値を変えてみると、グラフがなめらかな曲線で変化します。
※「99.線」の軸は 最小値:0、最大値:1 などで固定しておきましょう

今回「始点」は 0.5 で固定、「終点」のみディメンションに応じて高さを変えるようにします。
・終点の値を計算する
「終点」は 0 ~ 1 の間の値になります。以下の図は ディメンションが4つある場合の例になります。ディメンションが4つあるということは、最大値の 1 を4等分することになりますので、棒の距離は 0.25 になります。そして棒の中心はその半分の 0.125 ずれていることになります。

まずディメンションに応じて距離を計算します。
4.終点のサイズ:棒の距離を算出する計算フィールド

計算フィールド名: 4.終点のサイズ
1 / TOTAL(COUNTD([0.選択されたディメンション]))COUNTD([0.選択されたディメンション]) でディメンション数を個別カウントしていますが、総計が必要なため TOTAL で集計しています。表計算としては「1.パス」と「0.選択されたディメンション」での計算が必要になりますので、既定の表計算に追加しています。
そうすると以下のように棒の距離が計算されます。
続いて終点の位置を計算します。終点の位置は最初に棒の距離の半分、そのあとは棒の距離の値が追加されていきますので、累計で計算します。
5.終点の位置:棒の距離から終点の位置を算出する計算フィールド

計算フィールド名: 5.終点の位置
RUNNING_SUM([4.終点のサイズ]) - ([4.終点のサイズ] / 2)RUNNING_SUMで「4.終点のサイズ」を累計し、「4.終点のサイズ」の半分の値を引いています。そうすると以下のように終点の位置が計算できます。

先ほど「終点の位置を計算する」にて事前に計算した数字と一致しました。これで終点の位置の計算は完了です。
・曲線を描く
ここまでできれば、あとは Sigmoid関数 を利用して曲線の位置を計算するのみです。
6.線:曲線を描く計算フィールド

計算フィールド名: 6.線
[始点] + ([5.終点の位置] - [始点]) * [3.Sigmoid]これで全ての計算フィールドができました。なお「始点」のパラーメータについては、今回は固定で 0.5 にしておきます。早速配置しましょう。
まずは「1.パス」を 列 または 行 に置き、「欠落した値を表示」にチェックを入れて詳細に移動させます。

続いて「2.T」を列へ、「0.選択されたディメンション」を色に配置し、最後に「6.線」を行に配置します。すると見事に3つに枝分かれした点がプロットされました。

そしてマークを 線 に変更し、縦軸の「6.線」の高さを 0 と 1 に固定することで曲線の完成です。


■ダッシュボードを作成する
ダッシュボードを作るため、合計の売上のみのシート、曲線のシート、売上棒グラフのシートを作成ます。

棒グラフが売上順に並ぶように、「0.選択されたディメンション」を「並べ替え」で売上順にしておきます。ちなみに、曲線のシートは「昇順」に、棒グラフの方は「降順」にする必要があります。

作成した3シートをダッシュボードに配置すると完成です。シートを配置すると少し隙間ができると思いますので、パディングを 0 にするなどで調整しましょう。また、点の数を変えることで曲線のなめらかさも変わることを実感いただけると思います!

■最後に
いかがだったでしょう?かなり長くはなりましたが、当初の目標のようにイイ感じで曲線を描くことができました。実際に活用するシーンは限られてくるとは思いますが、是非良さげなダッシュボードができましたら共有いただけると幸いです。
★参考にさせていただいたサイト
勉強するにあたり Yoshitaka Arakawa様の「TABLEAUでSANKEY DIAGRAMを作る」を参考にさせていただきました。
大変参考になりました。ありがとうございました。
この場を借りてお礼申し上げます。
