
Kropki入門
はじめに
noteでは初めまして。初月葉桜(はづきはざくら)です。競技パズラーとしてパズルを解いたり、パズルの同人誌『トケタ?』シリーズの制作者の一人としてパズルを作ったりしています。今回は自己紹介はほどほどにして、本題に入りましょう。
この記事について
本日4/10から1週間、#ペンシルパズルデビュー週間 というイベントがPuzzle Aquare JP(以下、パズスク)にて始まります。簡単に言うと、「ペンシルパズルを初めて解く人や、初心者の方に向けた、簡単なパズルを投稿しよう」という趣旨のイベントになっています。
今回の記事は、このイベントに向けて投稿した自作のパズルの解説を記事にしてみよう、というものです。パズスクの作者コメント欄を活用することもできそうなのですが、丁寧に書くなら分量的にこちらの方が適していると思い、noteの初記事を兼ねて書いています。
それでは、さっそく解説に入ってみましょう。本日4/10特集のカテゴリは「数字配置のパズル」で、今回自分が投稿したパズルは、「Kropki(クロプキ)」というパズルです。
Kropkiのルール
どのタテ列・ヨコ列にも、1からNまでの数が1つずつ入るように、すべてのマスに、数を1つずつ書き入れます。(Nは、盤面の1辺のマス数)
マスとマスの間に白丸がある2つのマスでは、片方の数はもう片方の数より1大きくなります。
マスとマスの間に黒丸がある2つのマスでは、片方の数はもう片方の数の2倍になります。
マスとマスの間に丸のない2つのマスでは、片方の数がもう片方の数より1大きかったり、片方の数がもう片方の数の2倍になったりしません。
例題は、パズスクでルールを確認する際に一緒に出てくるので、ここでは割愛します。
パズスクのKropkiのページはこちら
投稿した問題の解説
パズスクに投稿した問題はこちらになります。
(リンクから進むとパズスク上で問題を解くことができます)

自分の経験則ではありますが、Kropkiを解く際のコツの1つとして、「丸の多い部分に注目する」というものがあります。丸のある場所では、片方の数字が決まればもう片方の数字の候補が多くても2通りに絞れるのに対し、丸のない場所では候補があまり減らないからです。ただし、ある程度数字が埋まっている盤面では、すでに埋まっている数字の情報と丸がないことを組み合わせて解き進められるような場面も存在します。
このコツを今回の問題でも使ってみます。まずは、上から1列目を見てみると、白丸が横に4つ連続しています。このように、白丸が同じ方向に連続している場合は、ある数字から1つ差で連続した数字が並んで入ります。

例えば、次の図で赤いマスに1が入ると、右隣のマスには2が入ります(Kropkiでは0は使いません)。

2の右隣のマスに入る数字は、1つ差の1か3が入りますが、すでにこの列には1が入っているので、3が入ります。
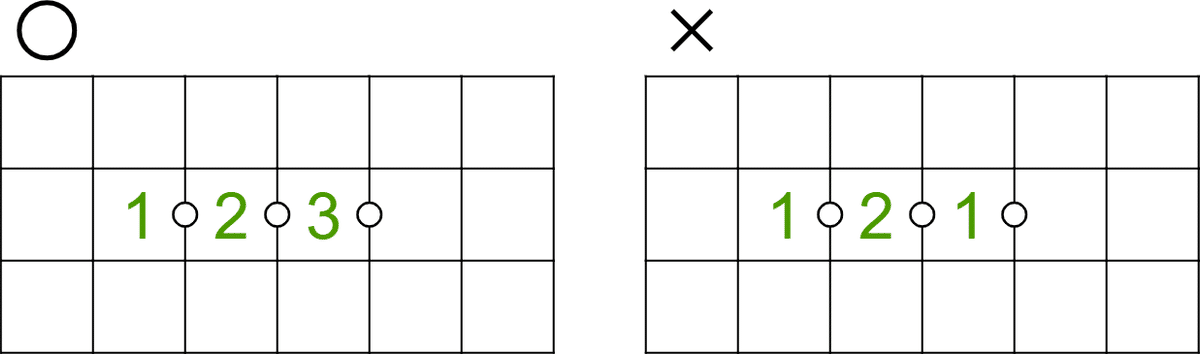
3の右隣のマスについても同様に考えると、2と4のうち、まだこの列に入っていない4が入ります。

これがずっと右端まで続いていくので、1,2,3,4,5のような連続した数字の並びができることになります。この例では、左端が2で右に3が入り2,3,4,5,……と1以外から始まるパターンや、左端が5で右に4が入り5,4,3,2,……と減っていくパターンもあります。共通しているのは、「白丸が連続した部分では、1つ差で連続した数が並んで入る」ということです。この性質は覚えておくと1つ違いナンプレなどを解く際にも重宝します。

さて、問題に戻ります。一番上のヨコ列は、左から1,2,3,4,5または5,4,3,2,1のどちらかのパターンになります。ここでは、真ん中の3だけが確定します。

次に、一番左の列に注目してみましょう。ここでは、黒丸がタテに2つ続いています。

黒丸は「2倍」のルールであるため、少ない個数であっても連続していればかなり有用なヒントになります。先ほど連続した白丸の性質を考えた時と同じように考えると、同じ列で連続して黒丸がある場所では、1,2,4,8,……のように、片方の端から連続して倍々になるように数が入っていくことがわかります。したがって、左端の列の黒丸が2つ続いた3つのマスは、上から1,2,4または4,2,1というパターンになります。これは、この問題のサイズが5×5で、6以上の数字が入らず、黒丸のある2マスに3,6や5,10という2つの数が入らないからです。少し難易度の上がった問題では、「この数字は黒丸のあるマスには入らない」ということを利用することもあります。なお、ここでも、真ん中のマスが2であることは確定します。

一番上の列と一番左の列で考えたことを同時に見てみると、左上の角のマスには1が入ることが分かります。したがって、一番上の列には左から1,2,3,4,5と入り、一番左の列には上から1,2,4と入ります(残りの3,5はまだ決まりません)。
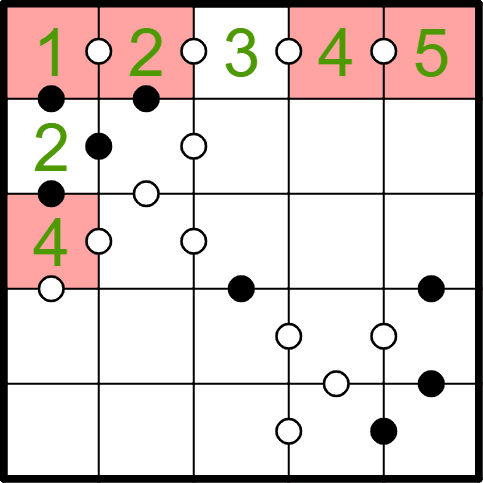
次は、上から3列目に2つ続いた白丸を見てみましょう。ここには4から始まる3つの連続した数、すなわち4,5,6または4,3,2という並びが入ります。しかし、このパズルで5より大きい数は入らないため、4,3,2の並びが入ります。

この列では残り2マスがまだ決まっていませんが、同じ列に同じ数字が入らないというルールを使うと、右上の角のマスに5があるので、左から4マス目が5,左から5マス目が1という風に決まります。
あるいは、丸のない場所についてのルールを使うと、今書いた2の右隣のマスには1は入らないので、5であると決めることもできます(2の隣に1が入る場合、その2マスの間には白丸か黒丸がないとルールに反するため)。

今書いた右端の1の下には黒丸が2つ続いているので、上から2,4と数字が埋まります。

右下の角の4の左隣のマスには、黒丸のルールより、2が入ります。また、右端の残り1マスには3が入ります。

今書いた3の左隣のマスを見ると、上下には4と5,左右には2と3があります。同じ列に同じ数は入らないので、ここには1が入ることが分かります。
「このマスに入る数字はこれしかない」という考え方は、数独・ナンプレでは少し難しい手筋として紹介されることもありますが、Kropkiは一般的にそれらのパズルよりサイズが小さく、それに伴って入る数字の種類も少ないので、この考え方も有用です。
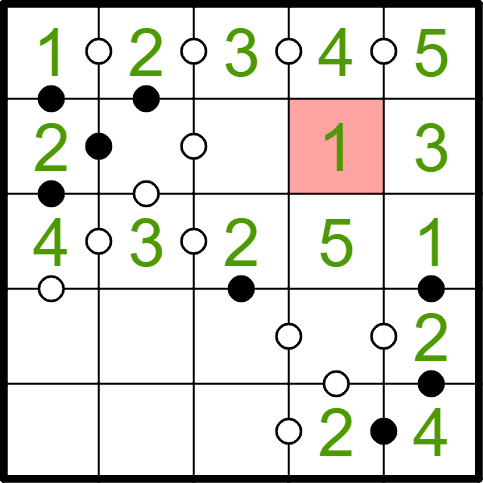
上から2列目の残りの2マスも、丸のヒントを使って埋めることができます。
また、上から4列目、左から4列目のマスも、左から4列目の残り1マスなので3が入ると決まります。

まだ使用していない丸のヒントがありますが、かなりのマスが埋まっているので、同じ列に同じ数が入らないことを使って最後まで解くことができます。例えば一番左の列では、上から4マス目に5が入り、一番下に3が入ります(左から4列目、上から4列目に3があるため)。

残り4つのマスも同じ要領で埋めると、すべてのマスが埋まり、このパズルを解くことができました。

おわりに
というわけで長くなりましたが初心者向けに解説記事を書いてみました。なるべく分かりやすく書いてみましたが、もし分かりづらい点があれば気軽にコメント等してください!また、「このパズル種の解説記事が欲しい」というリクエストもぜひどうぞ!なるべく答えてみたいと思っています。
明日以降も(筆者の時間と体力が許せば)解説記事を書いてみようと思っているので、よろしくお願いします!
