
統計学を装備する!14 〜ポアソン分布-課題1〜
ポアソン分布を学んだ。CHATGPTに課題を作らせて解いてみようぞ!
あっ、、、、、、、、いや特に。
1. ポアソン分布の基本理解
シナリオ:
ある会社のサポートセンターでは、1時間あたりの電話対応回数が平均 λ = 4回と記録されています。この情報をもとに、次の質問に答えてください。
課題:
1-1.1時間に電話がちょうど3回かかってくる確率を求めなさい。
(λ = 4、k = 3 を使って計算)
1-2: 1時間に5回以上の電話がかかってくる確率を求めなさい。
(λ = 4 を使って、5回、6回...を合計して求める)
学習目標:
ポアソン分布の基本的な公式を理解し、特定の回数が発生する確率を計算できるようになる。
実際の問題で、λを使って具体的な確率を計算するスキルを身につける。
解く手順
1.ポアソン分布の確率質量関数(PMF)を使って計算する。
解く
課題1-1.1時間に電話がちょうど3回かかってくる確率を求めなさい。
λ= 4
k=3
PMF(3,4) = 約0.195 = 約19.5%(答え)
課題1-2.1時間に5回以上の電話がかかってくる確率を求めなさい。
λ= 4
5回未満の確率を計算
PMF(0,4) = 約0.0183
PMF(1,4) = 約0.0733
PMF(2,4) = 約0.147
PMF(3,4) = 約0.195
PMF(4,4) = 約0.195
1時間に5回以上の電話がかかってくる確率 = P(X>=5)
P(X>=5) = 1 - 0.0183 - 0.0733 - 0.147 - 0.195 - 0.195
= 0.3714
= 約37.1% (答え)
これちなみに、、、λが大きいとどうなる?
λ(1時間あたりの平均電話回数)が10000とかだったらどうなるんか?
電話が10000回とか、もっと大きな回数になると、通常のポアソン分布の公式では計算が複雑になりすぎる。そんなときに使えるよき方法がある。
正規分布による近似
ポアソン分布のλ(平均)が大きくなると、ポアソン分布は正規分布に近似できる性質がある。具体的には、λが十分大きい(おおよそλ > 10くらい)場合には、次のように正規分布を使って近似できる:

つまり、平均 λ、分散 λの正規分布として扱える。このとき、ポアソン分布の代わりに正規分布を使うと、Zスコアを使って確率を計算できる。
ポアソン分布モデルを利用して確率を予測したい時、λとkが大きい場合に正規分布モデルを利用できてその際、平均と分散をλに設定すべしということ。
正規分布を使った計算の手順:
1.Zスコアを計算する。

2.計算したZスコアを使って、正規分布表から確率を求める。
解くと、k=3とすると、
Z = -99.97
CDF(累積分布関数 )(-99.97) = ほぼ0 (ほぼ0%)
あれ?
PMF(確率質量関数)(3,10000) = ほぼ0 (ほぼ0%)
計算できた?CDF使う意味ある?
調べると、、、、λ(平均発生率)と k ( 起こるイベントの回数)が大きいかつ、λとkが近い場合に正規分布の近似が利用するといいとのこと。
例えば、PMF(10003,10000)とか計算させると非常に大きな数値が発生して計算がオーバーフローした。
正規分布は連続型データを扱う分布だから、平均値周辺のデータを予測するのに強みを発揮する。ポアソン分布のλが大きくなると、正規分布で近似できる性質があるけど、それは主にλに近いk(回数)がターゲット。
ポアソン分布の公式
ポアソン分布の確率質量関数(PMF)の公式:
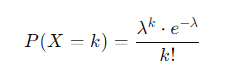
各パラメータの説明:
𝑃 ( 𝑋 = 𝑘 ) : k 回のイベントが発生する確率
λ : 一定期間内に平均して発生するイベントの回数(平均発生率)
k : 起こるイベントの回数(非負の整数)
e : 自然対数の底(約2.718)
k! : k の階乗
このポアソン分布の確率質量関数(PMF)も手計算は大変なのでソフトウェア使って計算させるのが一般的。CHATGPTに聞くのもあり。
使用例:PMF(ポアソン分布) = PMF(k, λ)
「X∼N(λ, λ)」という表現は、確率分布の記号表現。
この記号はこういう意味を持っている:
X:ランダム変数。何かのイベントの回数や結果がまだ確定していない変数。
∼N(λ, λ):これは正規分布に従うという意味。
「N(μ, σ²)」は、平均がμ(ミュー)で分散がσ²(シグマ二乗)の正規分布に従うことを示している。
つまり、X∼N(λ, λ)というのは、「ランダム変数Xは平均がλで、分散がλの正規分布に従う」っちゅうこと。
