細長比の感覚的理解

細長い部材の安定性を考える際、細長さが重要となる。その際、細長比（ほそながひ）という指標が用いられる。細長比$${λ}$$（ラムダ）は名前の通り物体の細長さを表し、数字が大きければ細長く、数字が小さければ図太くなる。

$$
λ＝\frac{L}{i}
$$

ここに$${L}$$は長さ、$${i}$$は断面二次半径である。断面二次半径の説明は別項に譲る。

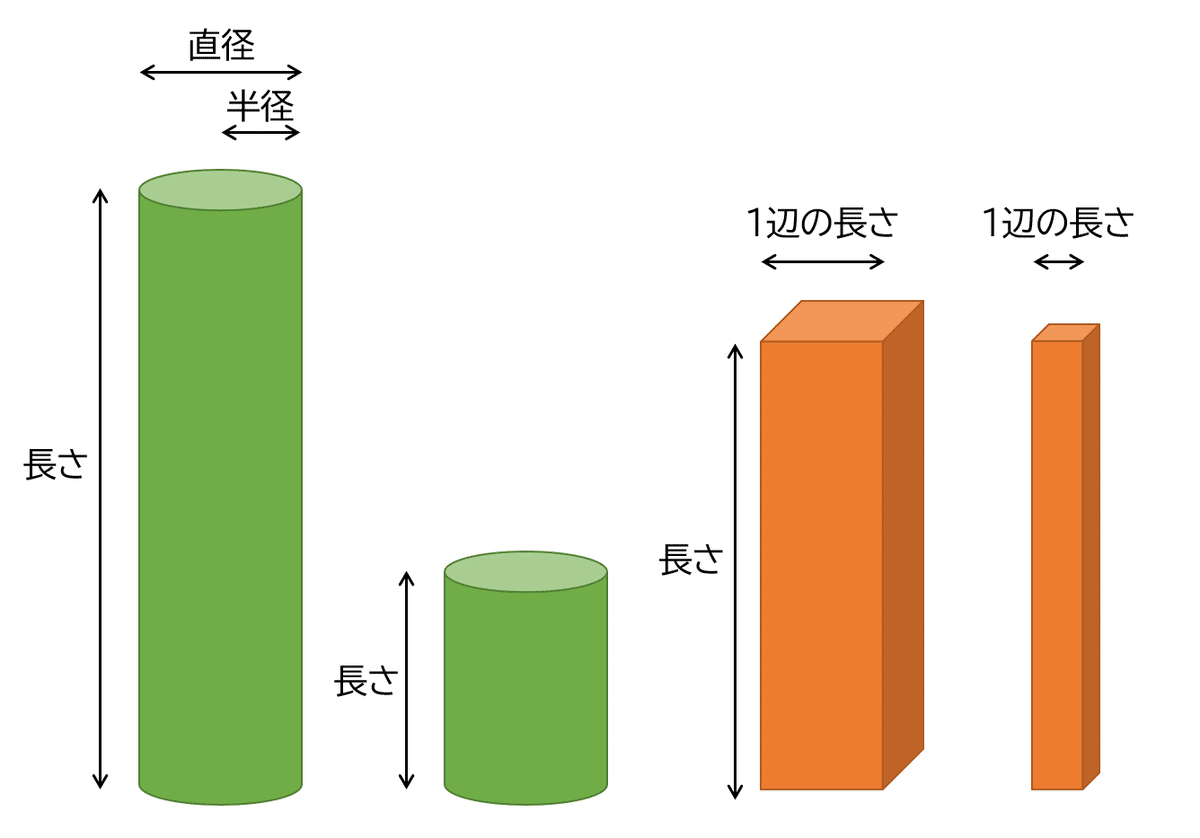
一般に、物体が細長いか、図太いかを判断する際に、長さと太さの比率を考える。下図のとおり、太さについては円柱であれば直径をイメージし、角柱なら1辺の長さをイメージするだろう。円柱の太さの指標としては、直径だけではなく、半径も使われることがある。細長さを表すときには統一した指標さえあれば、それが直径でも半径でも問題なく、要するに長さ方向と直角方向の2つの寸法が必要になることがわかる。

縦と横の比率

物体を曲げるということを考えたときには、物体の太さも関係するが、ここでは形状による曲げやすさ、曲げにくさを比較したい。

下図は、直径と長さの比率が、AとBは共通で1:9、CとDは共通で1:2の円柱である。高さはAとDで同じ、BとCで同じにしている。このとき、形状としての曲げやすさ・曲げにくさは、AとBで同じ、CとDで同じと考える。細長さ、図太さが同じと考えるのである。

長さと太さの比率

もちろん、太さの順に並べると、細い順にはB＜A＜C＜Dであるので、曲げるときの破壊力は、AとＢ、CとDでは同じにはならない。同じ長さでも細長さが異なると破壊力が違う、同じ太さでも細長さが異なると破壊力が違う、という風に、太さや長さとは別の指標として、細長さがある、と思うと良いだろう。

では、太さを表す指標には何を使えばよいか。物体は円柱だけでないので、円柱と角柱、そして任意の形をした断面を比較する際に共通の指標となることが望ましい。そこで登場するのが、断面二次半径である。