見出し画像

時系列基盤モデルによる株価データ(多変量)の類似度算出と検索

はち

1. はじめに

今回は時系列基盤モデルを使って、多変量の時系列データのEmbeddingを作成し、そこから時系列データ同士の類似度を算出するというのを試していきたいと思います。

元々、時系列データの類似度を算出する方法としては以下の２つがあったと思います。（時系列を専門にやってきたわけではないので間違っていたらご指摘お願いします。）

  • 動的時間伸縮法（DTW: Dynamic Time Warping）を利用して、単変量毎の類似度を算出。各次元の類似度を統合する。

  • LSTMなどのNNモデルを利用

しかし、前者は各次元間の関係性を考慮できていない、後者は学習が必要、という点で使いづらさがあったと思います。

時系列基盤モデルによって、学習なしに多変量時系列データのEmbedding化が可能になり、(言語)Embeddingモデルを使った時のように多変量時系列データの類似度が算出できるようになりました。
今回は、カーネギーメロン大学の１組織であるAutonLabによって公開されているMomentというモデルを、株価のデータに対して試していきたいと思います。
Nasdaqの直近の半年間の株価の推移が、過去のどの半年間の値動きと近かったかを検索してみます。

多変量時系列データの予測については過去の記事をご参照ください。

注意：この記事はあくまで技術的な記事であり、株の売買を推奨するものではありません。また、当該技術が株価の予測が可能であることを保証するものでもありません。売買はご自身の責任・判断で行なってください。当方は一切の責任を負いません。

2. 実施

実行環境はGoogle ColabのT4インスタンスです。

ライブラリのインストール

!pip install git+https://github.com/moment-timeseries-foundation-model/moment.git

時系列データの取得
今回は時系列データとしてNasdaqの株価チャートを使っていきたいと思います。取得にはyfinanceを使います。

import yfinance as yf

# データ取得
ndaq = yf.Ticker("NDAQ") 

# 株価データ(日毎)を取得(DataFrame形式)
hist_ndaq = ndaq.history(period="max")
hist_ndaq = hist_ndaq.reset_index(drop=False)
hist_ndaq

以下のようなDataframeが得られます。

株価データ（Nasdaq）

モデルの取得
task_nameにembeddingを指定します。

from momentfm import MOMENTPipeline

model = MOMENTPipeline.from_pretrained(
    "AutonLab/MOMENT-1-large", 
    model_kwargs={'task_name': 'embedding'},
)
model.init()
model.to("cuda:0")

株価データの分割
取得した株価データから、ステップ10毎に長さ128のデータを抽出していきます。Momentは512 timestepsまで入力可能ですが、そうすると約2年間の値動きの比較となってしまい、長すぎると感じたので128 timesteps（半年ほど）を指定しています。

def extract_segments(df, segment_length=512, step=10):
    """
    指定されたDataFrameから、指定した長さのデータセグメントを抽出します。

    この関数は、DataFrameの末尾から指定したステップサイズごとに
    指定した長さのデータセグメントを抽出し、それらのセグメントをリストとして返します。
    返されるリストは時系列順に並べ替えられます。

    Parameters:
    df (pd.DataFrame): 抽出対象のDataFrame。
    segment_length (int): 各セグメントの長さ（デフォルトは512）。
    step (int): セグメントを抽出する際のステップサイズ（デフォルトは10）。

    Returns:
    list of pd.DataFrame: 指定した長さのセグメントを含むリスト。

    Example:
    >>> segments = extract_segments(hist_ndaq)
    >>> for segment in segments:
    >>>     print(segment)
    """
    segments = []
    for start in range(len(df) - segment_length, -1, -step):
        segment = df.iloc[start:start + segment_length]
        segments.append(segment)
    
    # 取得されたセグメントを時系列順に並べ替え
    segments.reverse()
    return segments

segments = extract_segments(hist_ndaq, segment_length=128)
print(len(segments))

Embedding化
batch_size=128で実施して7秒で処理が完了しました。GPUメモリはかなり余っていたのでもっとバッチサイズを大きくしても良かったかもしれません。

from tqdm.auto import tqdm

def embed_segments(segments, model, columns=["Open", "High", "Low", "Close", "Volume"], batch_size=128):
    """
    指定されたセグメントリストをEmbedding化します。

    この関数は、各セグメントをEmbeddingモデルを使用してEmbedding化します。
    進捗状況はtqdm.autoを用いて表示されます。

    Parameters:
    segments (list of pd.DataFrame): 抽出されたセグメントのリスト。
    model (torch.nn.Module): Embeddingモデル。
    columns (list of str, optional): Embeddingに使用するカラムのリスト（デフォルトはNoneで全カラムを使用）。
    batch_size (int): モデルに渡すバッチサイズ（デフォルトは128）。

    Returns:
    list of torch.Tensor: 各セグメントのEmbeddingを含むリスト。

    Example:
    >>> segments = extract_segments(hist_ndaq)
    >>> embeddings = embed_segments(segments, model, columns=["Open", "Close"])
    >>> for embedding in embeddings:
    >>>     print(embedding.size())
    """
    embeddings = []

    # バッチ単位で処理するためのループ
    for i in tqdm(range(0, len(segments), batch_size), desc="Embedding Segments"):
        batch_segments = segments[i:i + batch_size]
        
        # 各セグメントをテンソルに変換し、バッチとして結合
        batch_tensors = []
        for segment in batch_segments:
            tensor = torch.tensor(segment[columns].values, dtype=torch.float)
            tensor = tensor.t().unsqueeze(0)  # 形状を (1, n_channels, context_length) に変換
            batch_tensors.append(tensor)
        
        # バッチテンソルを一つに結合
        batch_tensor = torch.cat(batch_tensors, dim=0)  # 形状を (バッチサイズ, n_channels, context_length) に変換
        
        # モデルにバッチテンソルを渡してEmbeddingを取得
        embedding = model(batch_tensor.to("cuda:0"))
        embeddings.extend(embedding.embeddings)
    
    return embeddings


columns = ["Open", "High", "Low", "Close", "Volume"]
embeddings = embed_segments(segments, model, columns)
print(len(embeddings))

類似度算出とランキング取得
現在(2024/6/6までの半年間)の値動きと近い値動きを過去にしているかどうか検索します。直近と近いと類似度が高くなることが考えられたので、barricade_num=10として、昨年くらいまでの中から検索を実施しました。

import torch
import torch.nn.functional as F

def find_top_k_similar_embeddings(embeddings, target_embedding, k=5):
    """
    指定されたターゲットEmbeddingに最もコサイン類似度が近いEmbeddingのインデックストップ5を辞書形式でリストアップします。

    Parameters:
    embeddings (list of torch.Tensor): Embeddingsのリスト。
    target_embedding (torch.Tensor): 比較対象のターゲットEmbedding。
    k (int): 上位k個の類似度を持つインデックスをリストアップします（デフォルトは5）。

    Returns:
    dict: 類似度が高いEmbeddingの順位をキーとし、indexと類似度を含む辞書形式のリスト。

    Example:
    >>> top_k_similarities = find_top_k_similar_embeddings(embeddings, target_embedding)
    >>> print(top_k_similarities)
    """
    similarities = []
    target_embedding = target_embedding.squeeze(0)  # Batch dimensionを取り除く
    
    for i, embedding in enumerate(embeddings):
        embedding = embedding.squeeze(0)  # Batch dimensionを取り除く
        cos_sim = F.cosine_similarity(embedding, target_embedding, dim=0)
        similarities.append((i, cos_sim.item()))
    
    # 類似度が高い順にソート
    similarities.sort(key=lambda x: x[1], reverse=True)
    
    # トップkのインデックスと類似度を取得
    top_k_similarities = {rank+1: {"index": index, "similarity": similarity} 
                          for rank, (index, similarity) in enumerate(similarities[:k])}
    
    return top_k_similarities


barricade_num = 10
target_embedding = embeddings[-1]
top_k_indices = find_top_k_similar_embeddings(embeddings[:-barricade_num], target_embedding)
print(top_k_indices)

グラフ出力
ロウソク足とValueの両方を出力します。

from plotly.subplots import make_subplots

def plot_candlestick_chart(df):
    """
    指定されたDataFrameを使用してローソク足チャートとValueのバーチャートを作成し、表示します。

    Parameters:
    df (pd.DataFrame): 'Date', 'Open', 'High', 'Low', 'Close'カラムを含むDataFrame。

    Returns:
    None
    """
    # Create figure with secondary y-axis
    fig = make_subplots(specs=[[{"secondary_y": True}]])

    # Candle sticks
    fig.add_trace(go.Candlestick(
        x=df['Date'],
        open=df['Open'], 
        high=df['High'],
        low=df['Low'], 
        close=df['Close'],
        showlegend=False,
    ), secondary_y=True)

    # Volume bar
    fig.add_trace(go.Bar(
        x=df['Date'], 
        y=df['Volume'],
        marker={
            "color": "rgba(128,128,128,0.5)",
        },
        showlegend=False,
    ), secondary_y=False)
    
    start = df['Date'].values[0].astype('datetime64[D]')
    end = df['Date'].values[-1].astype('datetime64[D]')
    fig.update_layout(
        title=f'Stock Price ({start} to {end})',
        xaxis_title='Date',
    )
    fig.update_yaxes(title="Price[$]", secondary_y=True, showgrid=True)
    fig.update_yaxes(title="Volume[$]", secondary_y=False, showgrid=False)
    fig.update_layout(xaxis_rangeslider_visible=False)

    fig.show()


# 最新
plot_candlestick_chart(segments[-1])

# 類似データ
for rank, top_k_index in top_k_indices.items():
    print(top_k_index)
    index = top_k_index["index"]
    plot_candlestick_chart(segments[index])

3. 結果

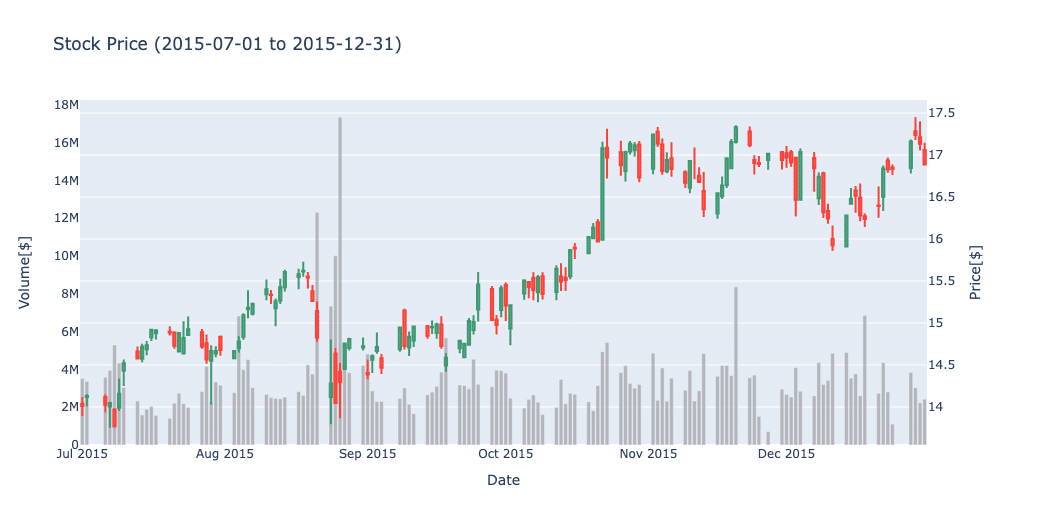
直近の区間と類似度が最も高かった区間のチャートを並べます。（2位から5位までのチャートはAppendixに貼っておきます。）

直近のNasdaqチャート
直近の値動きと類似度が一番高い区間（2019/3/13から9/12）

確かに、チャートの外形や直近の大陰線等似ているような気がするなと思います。
通常株価を扱う時は横軸は価格ではなくリターンとすることが多いですが、価格をそのまま扱ってきちんと類似度を測れるところがすごいなと思いました。（Transformerに入れられる際にスケールを調整する工程があるのだと思います。）

最後に、参考までに2019/9/12以降の値動きを確認します。
縦線が入っている位置が2019/9/12です。それ以降は10月頭を底として、11月後半に直近の高値をブレイクして上昇トレンドに入りました。
（注意：前述した通り、株の売買を推奨するものではありません。売買はご自身の責任・判断で行なってください。）

2019/9/12以降の値動き確認

4. まとめ

ある程度似たようなチャートを検索することができました。学習なしで多変量の時系列データの類似度を見れるようになるのは面白いなと思いました。こういった使い方も含めて、これから時系列基盤モデルの使い道が開拓されていくのだろうなと思います。

今回はDate, Open, Hight, Low, Close, Volumeを使いました。移動平均やボラリティ、ATR、MACDなどのよく使われる特徴量を追加するとまた変わってくるのかもなとも思いました。
また、特定の株価だけでなく、例えば為替や金利などのデータも含めて見るのも面白いと思います。

参照

Appendix

結果に貼りきれなかった2から5位までのチャートを貼っておきます。

直近の値動きと類似度が高い区間（2位）
直近の値動きと類似度が高い区間（3位）
直近の値動きと類似度が高い区間（4位）
直近の値動きと類似度が高い区間（5位）




いいなと思ったら応援しよう！