特徴量選択のための分散分析(ANOVA)
特徴量選択では「その特徴量により目的変数間の差があるか」を分散分析を用いて求め、特徴量の重要度を算出する手法が使われます。irisデータセットを使って実際に特徴量の重要度を計算していきます。
帰無仮説と対立仮説
帰無仮説を棄却し、対立仮説を採用することで、特徴量を選択します。
帰無仮説:この特徴量は目的変数間で差がない量である
対立仮説:この特徴量は目的変数間で差がある量である
帰無仮説が正しいとして検定を行います。あらかじめ、有意水準を設定しておき、有意水準よりも低い確率のことが起これば、それは極めて稀なことが起こったとして帰無仮説を棄却します。
irisデータセット
irisデータセットは以下のようなテーブルになっています。(一部)
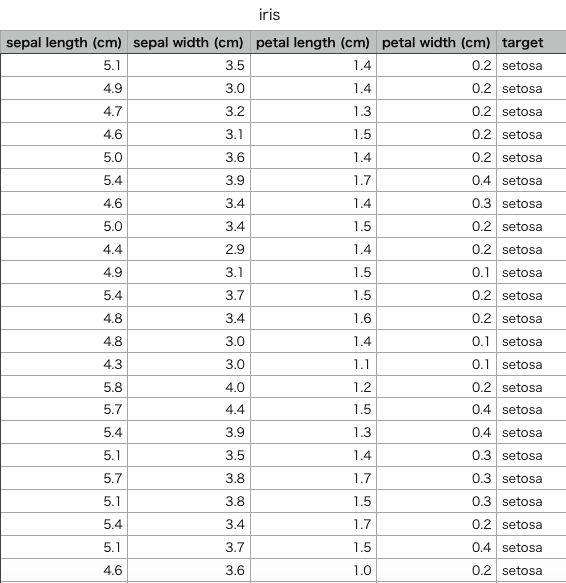
特徴量は4次元、データ数は150のデータセットになっています。
タイトル行は左から「ガクの長さ」「ガクの幅」「花弁の長さ」「花弁の幅」「花の種類」を表しています。
花の種類は「setosa」「versicolor」「virginica」の3種類です。
この4次元の特徴量のうち、花の種類の識別を行うのにどの特徴量が効果的かを算出するために、分散分析(ANOVA)を行なっていきます。
sklearnのfeature_selectionを用いてとりあえず実装
計算方法などを考えずにとりあえずライブラリを使って実装すると以下のようになります。
# 単変量統計
import pandas as pd
import matplotlib.pyplot as plt
# 特徴量の重要度を計算
from sklearn.feature_selection import SelectKBest
# f_classif:分散分析
from sklearn.feature_selection import f_classif
# データの読み込み
data = pd.read_csv('./iris.csv')
columns = ['sepal length','sepal width','petal length','petal width']
X = data.iloc[:,0:4]
y = data.target
# 分散分析の実行
selector = SelectKBest(f_classif, k=2) # kは選択する特徴量の数
X_new = selector.fit_transform(X, y)
# 各特徴量のF値を表示
print('feature importance: ', selector.scores_)
# 各特徴量のp値を表示
print('pvalues: ', selector.pvalues_)
# 可視化
# 属性とF値の結合
feature_scores = list(zip(selector.scores_,columns))
# 降順にソート
sorted_feature_scores = sorted(feature_scores,reverse=True)
num_list = []
col_list = []
for i in range(4):
num_list.append((sorted_feature_scores[i])[0])
col_list.append((sorted_feature_scores [i])[1])
plt.bar(col_list,num_list)
plt.xticks(rotation=45)
# 保存
#plt.savefig('feture_score.png')
<実行結果>
feature importance: [ 119.26450218 49.16004009 1180.16118225 960.0071468 ]
pvalues: [1.66966919e-31 4.49201713e-17 2.85677661e-91 4.16944584e-85]
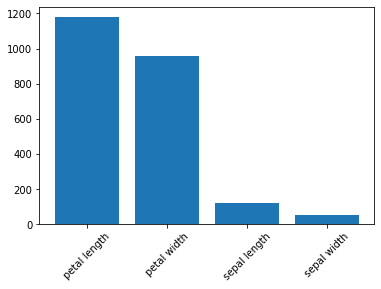
feature importanceはF値を表しています。
表は縦軸がF値、横軸が特徴量です。F値が大きい方が重要度の高い特徴量であると考えます。p値に関しては後述します。
F値の計算方法
<用語>
水準:目的変数の集合(今回は花の種類)
(1)各特徴量ごとに表を作成
sepal lengthの表はこんな感じです。タイトル行は目的変数(今回は花の種類)になります。これを特徴量の数だけ作成します。
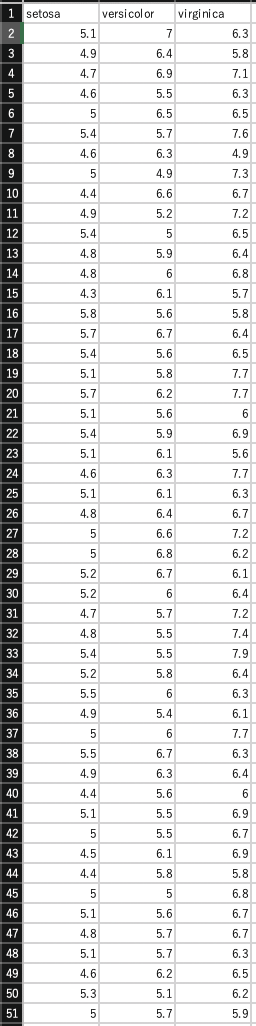
それぞれの表は以下のcsvをダウンロードするか、自分で作成してください。
(2)データの分布
とりあえず実装したときのF値が最も高かったpetal lengthと最も低かったsepal widthを例に分布を見ます。
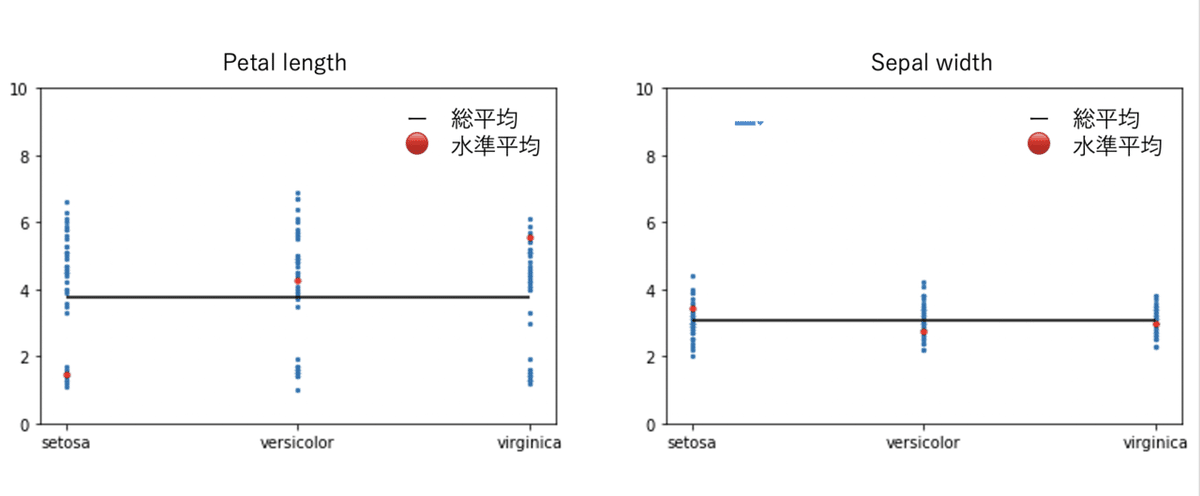
petal lengthは水準内でデータにばらつきがあるのが見て取れます。反対にsepal widthは水準内におけるデータのばらつきが少ないです。一見sepal widthの方が良い特徴量のように見えますが、水準間(水準平均🔴)のばらつきを見るとどうでしょう。petal lengthの方が水準間でばらつきがあるのがわかります。特徴量はその水準(目的変数)ごとに特徴的な値を持っていることが望ましく、言い換えれば水準間にばらつきがあることが望ましいということになります。
ここでは平均値に注目して視覚的に考察しましたが、次の項目では、分散分析表を用いてもう少し詳しく計算していきます。
(3)分散分析表
分散分析表の作り方は以下の通りです。


(2)では「水準間のばらつき」と表現しましたが、実際のF値は水準内変動に対する水準間変動の大きさを表しています。
ライブラリを使わずにpythonで実装
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 花の種類
target = ['setosa','versicolor','virginica']
# 水準数
a = 3
# 水準内データ数
n = 50
def anova(data) :
# 水準内平均を計算
in_average = []
in_average.append(data.loc[:,target[0]].mean())
in_average.append(data.loc[:,target[1]].mean())
in_average.append(data.loc[:,target[2]].mean())
# 総平均を計算
all_average = np.mean(in_average)
# 水準間平方和
Sa = 0
for i in range(a):
Sa += n*((in_average[i]-all_average)**2)
# 水準内平方和
Se = 0
for i in range(a):
for j in range(n):
Se += ((data.loc[:,target[i]])[j]-in_average[i])**2
# 水準間平均平方(水準間平方和/自由度)
Va = Sa/(a-1)
# 水準内平均平方(水準内平方和/自由度)
Ve = Se/(a*(n-1))
# F値
F = Va/Ve
return F
# データの読み込み
data_sepallength = pd.read_csv('./sepal length.csv')
data_sepalwidth = pd.read_csv('./sepal width.csv')
data_petallength = pd.read_csv('./petal length.csv')
data_petalwidth = pd.read_csv('./petal width.csv')
print('sepallengthのF値:',anova(data_sepallength))
print('sepallengthのF値:',anova(data_sepalwidth))
print('sepallengthのF値:',anova(data_petallength))
print('sepallengthのF値:',anova(data_petalwidth))<実行結果>
sepallengthのF値: 119.26450218450455
sepallengthのF値: 49.16004008961222
sepallengthのF値: 1180.1611822529803
sepallengthのF値: 960.0071468018062
ライブラリを使って実装した時と同じ結果になっているのがわかります。
どのくらいの値ならF値が大きいと言えるか
F値だけでは、特徴量の重要度の順番しか分かりません。順番は分かってもほとんどが必要のない特徴量である可能性もあります。逆にほとんどが重要な特徴量である可能性もあります。では、どのくらいの値ならF値が大きい(重要な)特徴量だと言えるのでしょうか。
F値は(水準間自由度,水準内自由度)のF分布に従います。
なので、今回は(4,147)のF分布に従うことになります。
どの特徴量を採用するかを判断するために、あらかじめ有意水準を0.05や0.01に設定しておきます。その値より大きいF値の特徴量は帰無仮説を棄却し、対立仮説を採用します。つまり、「その特徴量は目的変数間の差がある量である」とします。
from scipy.stats import f
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(1, 1)
# 水準間、水準内自由度
dfn, dfd = a-1 , a*(n-1)
# F分布を描画
plt.xlim(-1,26)
plt.ylim(0,1)
x = np.linspace(f.ppf(0.0000000001, dfn, dfd),f.ppf(0.9999999999, dfn, dfd), 100)
ax.plot(x, f.pdf(x, dfn, dfd), 'r-')
ax.axvline(f.ppf(0.95, dfn, dfd), ls = "--", color = "navy")
ax.axvline(f.ppf(0.99, dfn, dfd), ls = "--", color = "navy")
# 5%点の値(上側なので、95% を指定する)
print('上側確率 5%:', f.ppf(0.95, dfn, dfd))
# 1%点の値(上側なので、99% を指定する)
print('上側確率 1%:', f.ppf(0.99, dfn, dfd))
今回は、
sepallengthのF値: 119.26450218450455
sepallengthのF値: 49.16004008961222
sepallengthのF値: 1180.1611822529803
sepallengthのF値: 960.0071468018062
となったので、有意水準を0.01に設定した場合、全ての特徴量がF(0.01)=4.752より大きいF値となりました。
よって、今回は多クラス分類を行ううえで必要のない特徴量はないという結果になりました。しかし、特徴量の重要度はF値の大きい順なので、もし特徴量を半分に削減するとすれば、sepallengthとsepallengthを削減することになります。
irisデータセットではなく、もう少し汚いデータでやると面白いと思います。
時間があれば、特徴量の削減による分類精度の変化を加筆します。
