SVM理論偏(マージンの導出まで)
1.SVMとは
・SVM:Support Vector Machine
・機械学習(教師あり学習)の手法の一つ
・異なるクラスを識別する決定境界を定義し,その決定境界の間の距離を最大とする値を求める(マージン最大化)
・マージン最大化により過学習しにくいことがメリット
2.2クラス分類
説明を簡単にするため、2クラス分類を例に考える
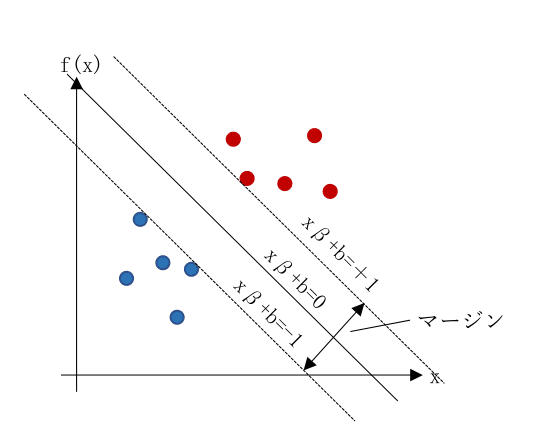
SVMによる2クラス分類では,f(x)=x・β+bにおいて,xに何かしらの数値を入力するとf(x)が1かー1 のどちらかを出力することによってクラス分類を行う.具体的には,入力 xに対して重みベクトルβをかけて,閾値 b を足したものが出力となる.重みベクトルβ,閾値 b に関してはラグランジュの未定乗数法を用いて求める.
3.マージンの導出
f(x)=x・β+bにおいて、βとbを求める
f(x_0) = x・β + b = 0
x・β =- b ...(1)
f(x_1) = x・β + b = 1
x・β = 1- b ...(2)
f(x_0)とf(x_1)の距離はマージンをLとすると、L/2で表される。
L / 2 = |x_1-x_0|
(L / 2) |β| = |x_1- x_0| |β| ...(3)
ここで、βは超平面の法線ベクトルなので、
|x_1- x_0| |β| = (x_1- x_0)・β ...(4)
(1)、(2)より
(x_1- x_0)・β = 1- b + b = 1 ...(5)
よって(3),(4),(5)より
(L / 2) |β| = 1
L = 2/|β|
