機械学習による株価予測 VS ドルコスト平均法
はじめに
こんにちは。noteで初投稿させていただきます。
製造メーカーの組み込みエンジニアとして働いている"はた"と申します。
普段はプログラミング言語ではC/C++をメインに扱っています。仕事柄、回路基板を扱うことも多く、回路図を読んだり、半田ごてを使って回路を作ったり、オシロスコープで測定したり…といったことをしております。
今回、Pythonによる機械学習の勉強を行ってきましたので、学習内容の振り返りを交えてここにアウトプットしようと思いました。これまでPythonに触れる機会がありませんでしたので、様々な機械学習向けのライブラリがあることを知って正直圧倒されています(笑)
機械学習に関しては初学者ですので、以降記載していきます内容が浅かったりする場合もあるかと思いますがご容赦のほどよろしくお願いします。
やりたいこと
機械学習による株価予測をやりたいと思っています。
理由は私自身が株式投資をしているため、株に興味があることに加えて、2024年からは新NISAがスタートするということもあり、最近のニュースにも大きく取り上げられている注目のテーマでもあると思ったためです。
また、株式投資では、よく「ドルコスト平均法」という言葉が出てきます。ドルコスト平均法とは、日々価格が変動する株や投資信託といった金融商品を常に一定の金額で、かつ、時間を分散して定期的に買い続ける手法のことです。
投資に使える時間が何十年もある若い方であれば時間を味方に付けてドルコスト平均法で長期に渡って買い続けることで、株式の平均取得単価を抑えることが期待できることと、一定の金額で定期的に購入する設定を行えば基本的には放置しておけばよいというメリットもあります。
今回、ある企業の株価の予測をしていくのですが、予測だけで終わるのではなく、せっかくなので「機械学習で株価予測して買う」のと、一般に良く知られる手法である「ドルコスト平均法で買う」のを比較すると、どのくらい差が出るのか検証できたら面白そうだなと思い、最後にこれを試してみたいと考えています。
実行環境
Visual Studio Code
Python 3.10.9
使用ライブラリは以下の通りです
・yfinance 0.2.14
・mplfinance 0.12.9b7
・pandas 1.5.3
・numpy 1.24.1
・matplotlib 3.7.0
・statsmodels 0.13.5
株価を取得してみる
まず初めに株価データを取得して、実際にデータを可視化しながらどういった機械学習にかけていくのかを考えていきたいと思います。
今回使用するデータは、私がメーカーに勤務していることもあるので、日本で最も有名なメーカーでもあるトヨタ自動車の株価を使用したいと思います。
株価データの取得には”yfinance“というライブラリを使います。
import yfinance as yf
# トヨタ自動車を指定
ticker = "7203.T"
# データを取得
df = yf.download(ticker, period = "max", interval = "1mo")上記のコードで株価を取得することができます。
変数tickerには今回使用するトヨタ自動車の銘柄コード(7203)を指定します。また、日本株を取得する場合は、銘柄コードに「.T」を付与することになっています。
download関数は様々な引数が指定できますが、上記においては株価を取得する期間(period)を最大(max)、頻度(interval)を1カ月(1mo)に指定してみることにしました。
それでは取得した株価を可視化していきたいと思います。

このように、download関数でperiod="max"を指定すると、1999年6月1日~2023年4月1日までの株価データを取得することができました。上記のデータにおいて、それぞれの列データは以下を表しています。
Date:取得日時
Open:始値
High:高値
Low:底値
Close:終値
Adj Close:調整後終値
Volume:出来高
続きまして、株価といえばローソク足と呼ばれる株価チャートが一般的ですので、そちらも可視化して株価の推移を確認したいと思います。
import yfinance as yf
import mplfinance as mpf
# トヨタ自動車を指定
ticker = "7203.T"
# データを取得
df = yf.download(ticker, period = "max", interval = "1mo")
# ローソク足の株価チャートを表示
mpf.plot(df, type="candle", volume=True, figratio=(10,5))上記のコードによって以下のような株価チャートを表示できます。

これでおおよそ20年ほどの期間の株価の推移を可視化できました。
データのトレンドはなんとなく緩やかな右肩上がりのチャートとなっており長期的に正のトレンドを形成しているように見えます。
また、周期的な変動については、上記のチャートを見る限りでは、8年前後の非常に大きな周期で株価の上昇と下降を繰り返しているように見えます。一方で、今回取得したデータは、月単位のデータを20年超の長期間で取得したことで、1年周期での特徴は見えにくくなっています。例えばperiodやintervalをより短くした上で可視化すると、1年周期での周期的な変動なども観測できるかもしれません。
なお、図の下側にある青いヒストグラムは月毎にどのくらい株の取引が行われたのかを示す出来高を示しています。今回の分析において出来高を使用する予定はありませんのでスルーしたいと思います。
定常性について
株価のように時間とともに変化するようなデータのことを時系列データといい、時系列データを分析することは様々な分野のビジネスでも使用されています。
時系列データを分析していく上では定常性の有無が重要と言われています。定常性がないデータを分析すると、全く意味のない相関関係を検出してしまうことがあります。そこで無意味な相関を検出しないように定常性のないデータは時系列データの階差を取るなどの変換を行い、定常性のある時系列データに変換してから分析を行う必要があります。
以上を踏まえて、まずは定常性とは何か?から説明したいと思います。
定常性とは、時間に依らず時系列データの期待値と自己共分散が一定である性質のことです。
期待値:確率論において1回の試行で得られる値の平均値のこと
共分散:2つのデータの間にある関係を表す値で、2つのデータがどれくらい相関関係を持ちながらばらついているかを表す
自己共分散:今のデータからある時点離れたデータとの間の共分散のこと
それでは定常性について式を使って理解を深めていきたいと思います。時系列データが定常性を持つ場合、以下の式①,➁が成り立ちます。
・期待値 $${E(y_t) = μ}$$ … ①
・共分散 $${Cov(y_t, y_{t−k}) = γ_k}$$ … ②
式①は、どの時点$${t}$$においても、$${y}$$の期待値が常に$${μ}$$を取るということを意味しています。期待値が一定であるため、時間の経過によらず一定の値を軸に変動しているイメージを持つと分かりやすいと思います。
式➁は、どの時点$${t}$$においても、$${k}$$次の自己共分散が常に$${γk}$$を取ることを意味しています。自己共分散が一定ということはデータのばらつきが一定ということですので同程度の幅で振れて変化するイメージになります。
ホワイトノイズとは
次に、ホワイトノイズについて説明したいと思います。
ホワイトノイズは、時系列データを表すときの確率的なばらつきを表現する際に利用され、時系列解析を行うモデルにおいても頻繁に登場するためどのようなものか説明を行いたいと思います。
以下の式③,④,⑤が成り立つとき、$${εt}$$をホワイトノイズといいます。
期待値 $${E(ε_t)=0}$$ … ③
分散 $${Var(ε_t)=σ^2}$$ … ④
k次自己共分散 $${γk=E(ε_t,ε_{t-k})=0(k≠0)}$$ … ⑤
式③,④,⑤を見ると、ホワイトノイズは期待値が0であり、分散$${σ^2}$$を持ち、$${k}$$次の自己共分散が0であると分かります。これらから性質から前項の「定常性について」で説明したようにホワイトノイズは定常性を満たすことが分かると思います。
では、実際にホワイトノイズがどのようなものか出力してみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
# ホワイトノイズの設定
mean = 0
std = 1
data = np.random.normal(mean, std, size=100)
# ホワイトノイズのプロット
plt.title("Whitenoise")
plt.plot(data)
plt.show()コードを実行すると以下のようなグラフが得られます。
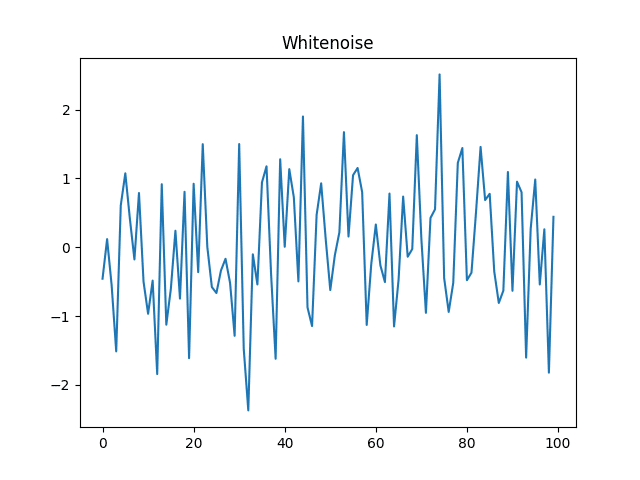
このように、平均0で標準偏差1である何の自己相関もないノイズを生成することができます。
ホワイトノイズは時系列データを表すときの確率的なばらつきを表すために用いられます。例えば、今回分析する株価チャートは確率的なばらつきを持つためギザギザとしたグラフになりますが、上記のようなホワイトノイズ$${ε_t}$$を加えることで確率的なばらつきを表現することが可能です。
時系列解析モデル
株価予測を行うにあたり、使用するモデルを決定する前に、時系列解析を行うモデルについて紹介し、それぞれの特徴を簡単にまとめていきたいと思います。
MAモデル
MAモデルは時系列解析モデルのひとつで、英語のMoving Averageの頭文字とっていることから移動平均モデルとも呼ばれます。以下では1次MAモデルおよび2次MAモデルを例に説明を行っていきたいと思います。
1次MAモデル、2次MAモデルは期待値$${μ}$$、ホワイトノイズ$${ε_t}$$とすると、それぞれ以下の式⑥,➆で表されます。
$${y_t=μ+ε_t+θ_1ε_{t−1}}$$ … ⑥
$${y_{t-1}=μ+ε_{t-1}+θ_1ε_{t-2}}$$ … ➆
上記の式⑥,➆から$${k}$$次のMAモデルは期待値$${μ}$$、時点$${t}$$から$${t−k}$$におけるホワイトノイズと定数項$${θ}$$との加重和によって表現されています。式からもMAモデルは不規則変動(誤差)として用いられるホワイトノイズが重要な役割を担っていることが分かります。
また、$${q}$$次のMAモデルを$${MA(q)}$$ と表し、$${MA(q)}$$は過去の不規則変動に影響されるモデルであり、$${q}$$次前までは自己相関を持ち、$${q+1}$$次前のデータとは自己相関を持たないという性質を持ちます。
MAモデル自体は実世界において単体で使用されることは少ないと聞きますが、MAモデルと次に紹介するARモデルを組み合わせたARIMAモデルとSARIMAモデルはビジネス分野等で分析に用いられるそうです。
ARモデル
ARモデル(AutoRegressive Model)は自己回帰モデルとも呼ばれ、現在の値を過去のデータを用いて回帰するモデルです。1次のARモデルを式で表すと以下のようになります。
$${y_t=c+φy_{t-1}+ε_t}$$ … ⑧
式⑧に示されるように、$${y_t}$$ がそこから一時点ずらした $${y_{t−1}}$$ で表されるため自己相関が表現されます。直前の$${p}$$個の値から次の値を予測するARモデルを$${AR(p)}$$ と表現します。
ARMAモデル
MAモデルとARモデルを組み合わせたモデルであり、$${ARMA(p,q)}$$と表されます。$${Σ}$$を用いてARMAモデルの式を表現すると以下のようになります。
$${y_t=c+ε_t+\displaystyle\sum_{i=1}^pφ_iy_{t−i}+\displaystyle\sum_{i=1}^qθ_iε_{t−i}}$$ … ⑨
式⑨を見ると、ARMAモデルが$${p}$$次のARモデルと$${q}$$次のMAモデルから構成されていることがよく分かると思います。
ARIMAモデル
ARIMAモデルは時系列データのd時点前との階差をとった系列、すなわち$${y_t–y_{t–d}}$$をARMAモデルで表したモデルであり、$${ARIMA(p,d,q)}$$と表記します。
$${ARIMA(p,d,q)}$$を式で表すと以下のようになり、ARMAモデルの式⑨と比較すると、左辺に表わされる$${d}$$次の階差系列を右辺のARMAモデルによって表現していることが分かると思います。
$${y_t-y_{t-d}=c+ε_t+\displaystyle\sum_{i=1}^pφ_iy_{t−i}+\displaystyle\sum_{i=1}^qθ_iε_{t−i}}$$ … ⑩
また、時系列データの分析にあたり、意味のない相関関係を検出しないよう定常性が重要であることを説明しましたが、ARIMAモデルは非定常過程(時系列データの期待値や分散が時間に依存している過程)にも適応できる点がポイントになります。
SARIMAモデル
SARIMAモデル(Seasonal ARIMAモデル)とはARIMAモデルをさらに季節周期を持つ時系列データにも拡張できるようにしたモデルであり、SARIMAモデルは$${(p, d, q)}$$のパラメーターに加えて$${(sp, sd, sq, s)}$$というパラメーターを持ちます。
ARIMAモデルは時系列方向に対して$${ARIMA(p,d,q)}$$を使用するモデルですが、SARIMAモデルは、さらに季節周期$${s}$$方向に対しても$${ARIMA(sp,sd,sq)}$$によって表現するモデルと捉えることができます。
上記の通り、SARIMAモデルはパラメータが合計7個ありますから、実際に使用する際には、その組み合わせが爆発的に増加しないようなパラメータを設定することがよく行われます。
具体的には、予め分析する時系列データを可視化する等によって周期$${s}$$を決め打ちして、$${sp, sd, sq}$$は低く抑えるといったことが行われます。
今回用いているPythonには、これらのパラメータ$${(p, d, q, sp, sd, sq, s)}$$を自動で適切に設定する仕組みはないそうです。そのため、AIC(赤池情報量基準)やBIC(ベイズ情報量基準)といった情報量基準に基づいて、どういった組み合わせが適切なのかを調べて決定する必要があります。
データを可視化・分析する
時系列データを扱うとき、原系列がトレンド(傾向変動)・季節変動・不規則変動という3つの基本成分の合成から成り立つという捉え方があります。この合成の方法を加法モデルとして捉え、トレンドを$${T(t)}$$、季節変動を$${S(t)}$$、不規則変動を$${e(t)}$$とおくと、原系列$${O(t)}$$は以下の式で表すことができます。
$${O(t) = T(t) + S(t) + e(t)}$$ … ⑪
上記のように時系列データを捉えたとき、不規則変動を定常性のあるホワイトノイズで当てはめれば、原系列が定常性を有しない理由として挙げられる要因は、トレンドと季節変動ということになります。
例えば、時系列データが正のトレンドを持っていれば、その期待値$${E}$$は上昇傾向を持つということになり、式①を満たさないので定常性があるとは言えません。
また、ある時期(季節)のみデータが急激に増減するような時系列データは$${k}$$次自己共分散が常に$${γk}$$を取る式➁を満たさないため定常性があるとは言えません。
このように加法モデルで時系列データを捉えると、式⑥を変換することで、
$${e(t) = O(t) - T(t) - S(t)}$$ … ⑫
となるため、不規則変動$${e(t)}$$は原系列からトレンドと季節変動が取り除かれた定常性のある時系列データと言えます。
では、ここまで説明したところで今回時系列データとして使用するトヨタ自動車の株価データについて、トレンド・季節変動・不規則変動の基本成分がどうなっているのかを可視化してみたいと思います。
原系列を基本成分に分解するには statsmodels の seasonal_decompose() 関数を使用します。この関数はリンク先のドキュメントにも記載されている通り、移動平均を用いてトレンド成分を求め、原系列からトレンドを除去して周期成分を求めるという比較的単純な方法を扱っています。
例えば、時系列データに12カ月ごとの季節変動があった場合、12個のデータで移動平均を求めることで季節変動が除去され、トレンドを推定することができます。さらに、このトレンドを差し引くことでトレンド成分を除去することにより、定常性のある時系列データを得ることができます。
import yfinance as yf
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
# ターゲットを指定
ticker = "7203.T"
# データを収集
df = yf.download(ticker, period = "max", interval = "1mo")
# データを成形
stock_close_df = df['Close']
# データを基本成分に分解する
decompose_result = seasonal_decompose(stock_close_df, model="additive", period=12 )
decompose_result.plot()
plt.show()上記のように seasonal_decompose() 関数は、modelにadditive(加法モデル)を指定し、ひとまずperiodには12カ月を設定します。
コードを実行すると以下のような基本成分を可視化することができます。

グラフの見方ですが、上から原系列、トレンド(傾向変動)、季節変動、不規則変動 (残差) になります。
ローソク足の株価チャートを可視化した時には、20年超の長期間の株価データを扱っていることもあり、1年間の季節変動が分かりにくかったですが、季節変動があることが見て取れます。
また、不規則変動(残差)に着目すると、2008~2009年頃と2016年頃にひと際下がっている点があります。2008~2009年頃と言えばリーマンショックがあり、景気に大きな影響を与えた時期でした。2016年頃はイギリスのEU離脱がニュースとなり、先行きの不透明感から安全資産の円が買われたことで円高となり輸出企業である自動車メーカーの株価が下がった時期です。
このように、基本成分を可視化することで様々な情報を得ることができますし、statsmodels の seasonal_decompose() 関数であれば簡単に上記のような結果を得ることができますから、時系列データを扱う際はその特徴を確認する目的でまず使ってみるのがいいと思います。
一方で、移動平均を用いた手法のため、データが無く移動平均を計算することのできない両端部には欠損が発生しますから、開始時点と終了時点ではトレンドと不規則変動を描くことができていないことが上記のグラフからも分かると思います。
モデルの選定をする
ここまででトヨタ自動車の株価データについて可視化を行い、時系列データの特徴を捉えることができましたので、それを踏まえて、どういった方法を用いて株価を予測するのかモデルを選定したいと思います。
時系列解析モデルとして、MA、AR、ARMA、ARIMA、SARIMAモデルの5つについて説明を行いましたが、今回分析するトヨタ自動車の株価データは前項で可視化したように、季節変動が見られることからSARIMAモデルによって株価の予測を行ってみたいと思います。
機械学習による株価予測をしてみる
さっそくSARIMAモデルを使って株価データを予測したいと思います。
上記で説明したように、SARIMAモデルは初めにパラメータ$${(p, d, q, sp, sd, sq, s)}$$を決定する必要があります。周期に関しては、時系列データの可視化によって12カ月の季節周期を認められるため、周期$${s=12}$$で決め打ちしたいと思います。
周期以外のパラメータに関しては、指定した範囲のパラメータの全ての組み合わせに対して学習を行い、もっともよい精度を示したパラメータを採用するグリッドサーチという方法を使用します。
指定するパラメータの範囲ですが、パラメータの個数と指定する範囲を大きくすれば組み合わせは爆発的に増加しますので、コンピュータ性能なども踏まえて決定すればよいと思います。
今回の株価予測においては、全てのパラメータについて0~1の範囲で、BIC(ベイズ情報量基準)を用いたグリッドサーチによって最適なパラメータの組み合わせを見つけていきます。
import itertools
import pandas as pd
import numpy as np
import yfinance as yf
from statsmodels.tsa.statespace.sarimax import SARIMAX
# ターゲットを指定
ticker = "7203.T"
# データを収集
df = yf.download(ticker, start = "2000-01-01", end = "2020-01-01", interval = "1mo")
# データを成形
stock_close_df = df['Close']
def selectparameter(DATA,s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = SARIMAX(DATA, order=param, seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs,results.bic)
except:
continue
return parameters[np.argmin(BICs)]
# グリッドサーチで最適なパラメーターを求める
param = selectparameter(stock_close_df, 12)
print(param)上記を実行すると以下のようなパラメータが得られました。
$${( p, d, q, sp, sd, sq, s ) = ( 0, 1, 0, 0, 1, 1, 12 )}$$
それでは、得られたパラメータをSARIMAモデルに設定して株価を予測してみます。
ここでは2000年1月から2019年12月までの240個のデータを訓練データとして使用します。そして、訓練データによって学習を行い、推定されたモデルにより2015年1月から2022年12月までの96個のデータの予測値を取得して、2000年1月から2022年12月までの276個のデータと重ね合わせたグラフを作成したいと思います。
import matplotlib.pyplot as plt
import yfinance as yf
from statsmodels.tsa.statespace.sarimax import SARIMAX
# ターゲットを指定
ticker = "7203.T"
# データを収集
df = yf.download(ticker, start = "2000-01-01", end = "2023-01-01", interval = "1mo")
# データを成形
all_data = df['Close']
# 訓練データを分割
train_data = all_data[:240]
# モデルの構築
model_fit=SARIMAX(train_data,order=(0,1,0),seasonal_order=(0,1,1,12)).fit()
# 予測値を取得
pred_data = model_fit.predict("2015-01-01","2022-12-01")
# 描画
plt.plot(all_data)
plt.plot(pred_data,color="r")
plt.show()グラフを描画した結果は以下の通りになります。
赤線の方が予測値です。

上記のように、予測値の内、訓練データとして使用している期間に関してのフィッティングは良いですが、訓練データ以外の期間(2020年1月以降)は、全体的な右肩上がりの傾向は掴んで予測できているといった感じでしょうか。
機械学習 VS ドルコスト平均法の検証
ここまでくるのに長かったですが、冒頭で説明したように「機械学習で株価予測して買う」のと「ドルコスト平均法で買う」のを比較すると、どのくらい差が出るのかを検証をしていきます。
検証の方法によって結果も変化してくると思われるため、その点には留意しつつ、今回はSARIMAモデルの予測データの内、訓練データと被っていない期間である2020年1月~2022年12月の36カ月の期間を使用します。
比較の方法は、1年間に株式を取得する金額を設定した上で、SARIMAモデルの予測データの方は1年間で最も株価が安いと予測した月に全額を使用して株式を取得します。一方、ドルコスト平均法の方は、毎月同じ金額で株式を取得する方法とします。最終的に2022年12月時点において、どちらの方法が優位であったかを検証したいと思います。
import yfinance as yf
from statsmodels.tsa.statespace.sarimax import SARIMAX
# ターゲットを指定
ticker = "7203.T"
# データを収集
df = yf.download(ticker, start = "2000-01-01", end = "2023-01-01", interval = "1mo")
# データを成形
all_data = df['Close']
# 訓練データとテストデータに分割
train_data, test_data = all_data[:240], all_data[240:]
# モデルの構築
model_fit=SARIMAX(train_data,order=(0,1,0),seasonal_order=(0,1,1,12)).fit()
# 予測値を取得
pred_data = model_fit.predict("2020-01-01","2022-12-01")
# 1年あたりの取得金額を設定
amount_of_money_per_year = 1200000
# ドルコスト平均法で取得
holding_stock_num_by_dollar_cost_ave = 0
amount_of_money_per_month = amount_of_money_per_year / 12
for sp_test in test_data:
holding_stock_num_by_dollar_cost_ave += ( amount_of_money_per_month / sp_test )
print("ドルコスト平均法による取得株式数:", holding_stock_num_by_dollar_cost_ave)
# SARIMAモデルによる予測で取得
holding_stock_num_by_SARIMA_pred = 0
stock_price_min = 0
index = [0, 0, 0]
# 購入する月(インデックス)を探索する
for i, sp_pred in enumerate(pred_data):
if i % 12 == 0 :
stock_price_min = max(pred_data)
if( sp_pred < stock_price_min ):
stock_price_min = sp_pred
index[(i//12)] = i
# 探索した月で取得する
for i in index:
holding_stock_num_by_SARIMA_pred += ( amount_of_money_per_year / test_data[i])
print("機械学習による取得株式数:", holding_stock_num_by_SARIMA_pred)コードの実行結果は以下の通りとなりました。

上記の数値は同じ金額を使って取得することができた株式数を表していますので、数値の大きかった方が優位であることになります。
以上の結果から、あくまで今回の検証の条件下においてになりますが、ドルコスト平均法の方が取得株式数が多かったため、ドルコスト平均法の方に優位性があるという結果になりました。
今回のSARIMAモデルによる検証は、ハイパーパラメータを特定の範囲から決定したり、季節変動12カ月設定での決め打ちの方法を使っていますので、これらを更に最適化することで、例えばローソク足のチャートを可視化した時に発見した、8年前後の大きな周期での株価のうねりを予測・再現することができれば優位性にも変化が生じるのではないかと思いました。
最後に
今回、初めて機械学習を学び、株式投資に当てはめて検証を行う中で感じたことをまとめたいと思います。
1.目的
機械学習は手段であり、どういった目的を達成したいかという点が重要だと感じました。目的によっては機械学習を使用する必要がないことも実際にはあると思いますので、そういった見極めも重要なのではないかと思いました。
2.数式の理解
Pythonのライブラリで比較的簡単に機械学習モデルを扱うことができますが、それだけでは何をやっているかわからないので、モデルの数式を理解することも大切だと感じました。
3.機械学習の種類
今回は時系列解析モデルを用いましたが、機械学習には様々な種類があるため株価の予測に対して他の方法も使えると思います。こういった点からも、学習した機械学習モデルをまずは実際に試していくとよいかなと感じました。
