尺取り法
atcorderで解けなかった問題の解説とアルゴリズムの解説を行っていきます
今回は尺取り法について
尺取りほうが使えるのは以下の通り
1.条件を満たす最大の範囲
2.条件を満たす最小の範囲
今回は1を用いた解説をしていくよ
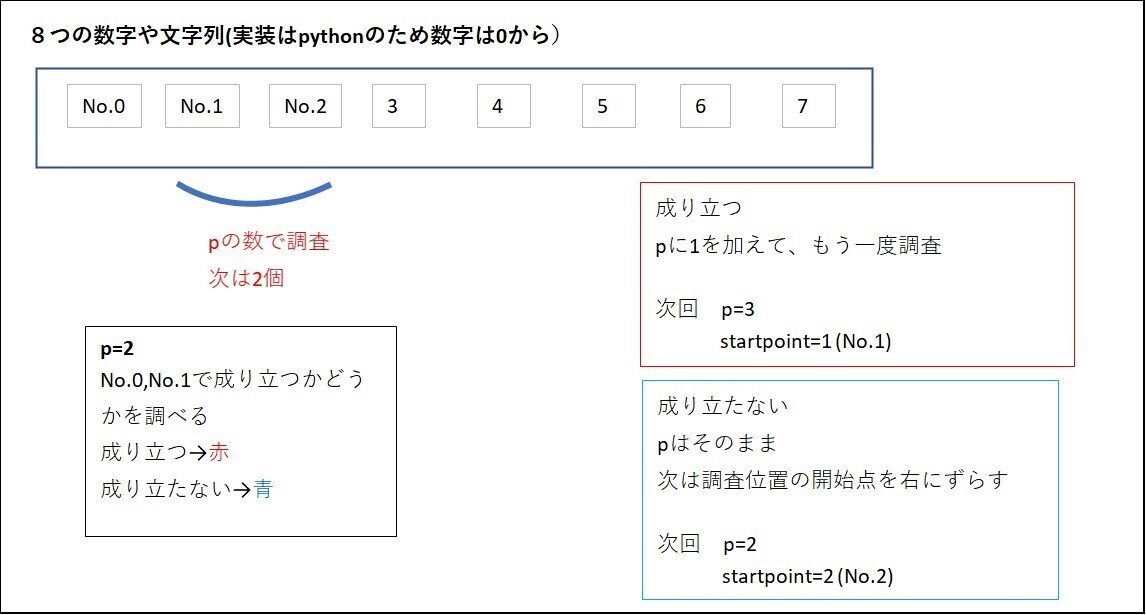
尺取り法の原理
pの数は満たすかどうかを判断し、満たすならp+1して満たさないなら、一つ右の文字列へ移動することで次に満たす場所を探すということを繰り返していくという方法である
求めるのはp-1ということに注意すべきだろう

次は上の場面で成り立った場合を考えてみる。

上の場面で成り立たなかったとすると
隅まで、実験を行う
pは成り立たない状態で右にスライドする。
成り立つときは調査列を増やすことで最大の幅を求めていく
続いて例題を見ていこう
例題 atcorderより ABC229 D問題 Longest X
(参考)https://atcoder.jp/contests/abc229/tasks/abc229_d
問題文
X と . からなる文字列 S が与えられます。
S に対して、次の操作を 0 回以上 K 回以下行うことができます。
. を X に置き換える
操作後に、X を最大で何個連続させることができますか?
解法ヒント
この問題の特徴はstartpointに加え、endpoint及び、ドットの累積のリストを用いることでS内の' . 'の数を求めることができる。
python 正解コードは以下
S=input()
N=int(input())
def check(s):
cnt=0;count=[0]
for n in range(len(S)):
if S[n]=='.':
cnt+=1
count+=[cnt]
# print(count)
startpoint=1;endpoint=1
while startpoint<=len(s) :
while startpoint<=len(s):
# print('start',startpoint,endpoint)
if count[startpoint]-count[endpoint-1]>N:
# print('break',startpoint,endpoint)
break
# print('roop',startpoint,endpoint)
startpoint+=1
startpoint+=1
endpoint+=1
p=startpoint-endpoint
return p
print(check(S))これによって、求められる
自分がはまったポイントは、累積数を入れたリストからstartpointとendpoint間のドットの数を求めるときにcount[endpoint-1]で求められる点である。
count[n]でn=endpointで計算すると、endpoint上のドットが数えられていない。よってn=endpoint-1で行わないといけない。

p-1しないのはなぜかという問題ですが、
(7-4)+1=4
よってp=4となるのですが、4つは成り立たないラインの数字なので
3が答えとなる。
p= endpoint-startpoint
以上で終わりです。
例題は自分の理解ができるようになるために乗っけているのでだんだんと増えていくかもしれません。
