
限界耐力計算:伝統構法に向いた耐震設計法+耐震性能評価計算
■限界耐力計算:伝統構法建築に向いた耐震設計法。
建物が地震の力を受けたとき、地盤や建物の状況をちゃんと把握して計算する優れた計算方法。
地震により、建物が損傷して変形し、そのまま倒壊するのか、それともどの程度まで耐えるのかを計算により判断する方法。
□伝統構法の建物について言われていること
:伝統構法は柔構造だから地震に強い
:伝統構法は地震の力を受け流すから強い
:伝統構法は石場建てだから強い
:建物と地面が直結していないので地震力の入力を低減する
:伝統構法の建物は総持ちである(組上がった部材などが総合的にからみあって、荷重を支えている)
:伝統構法は建物全体で揺れを分散させるので崩壊しにくい
:仕口や継手が関節のようにある程度動かないと力を吸収できない
:伝統構法は免震構造である
:古い建物が何百年も建ち続けているのが強さの証明
→根拠を持つことが必要
■建築基準法で、伝統構法は置いて行かれている。
■伝統構法木造建築物に「限界耐力計算」が使われる理由
1.石場建て、金物不使用など建築基準法の仕様規定に合わないから
2.建物の固有周期が長い。動きが違うのを評価する
3.建物の構造的特徴が「限界耐力計算」で活かすことができる
:開放的な間取り(壁が少ない)
:貫や差鴨居、長ほぞ、落とし込み板壁
:垂れ壁、腰壁
:太い柱(傾斜復元力)、大きな梁
:格子板壁
■建築物の地震に対する安全性を検討するには(基本)
1.建物の耐力を計算する
2.建物に入力される地震力を計算する
3.両者の力を比較する
:建物の変形により建物の耐力は変わる
:建物に入力される地震力も建物の変形により変わる(小さくなる)
建物が変形すると固有周期が長くなる。建物の固有周期が長くなると、建物に入力される地震力が小さくなる。地震力より建物耐力のほうが大きくなり、変形はその時点で止まる。
■地震力より、建物の耐力が大きければ建物は倒壊しない。
■建物が、どういう状態(変形角)の時に、地震力より建物の耐力が大きくなるかを調べる。
■具体的には、建物の層間変形が1/120、1/60、1/30、1/15の時を検討する。
(高さH=3Mとして、1/120(25mm)、1/60(50mm)、1/30(100mm)、1/15(200mm))
■地震力の低下を利用するためには、
:建物の変形が進んでも耐力が落ちないこと
:仕口・継手に変形性能があり、こわれないこと。めり込みながら耐える。ことが必要。
:在来工法の安全ゾーンは1/30、伝統構法の安全限界が変わるゾーンは1/15
■限界耐力計算の概要 まとめ
:現代型木造住宅は剛性が高く、固有周期が短い。変形して固有周期が長くなる前に接合部が壊れる。だから耐力勝負するしかない。
(限界耐力計算をしても意味がない)
:開放的な間取りを活かした住まいを作るためには、少ない耐震要素をうまく活用する必要がある。それができる計算方法が限界耐力計算である。
:開放性の高い伝統構法の建物を現行の仕様規定でチェックするのは、超高層の建物を一般の中高層洋の基準で計算するようなもの。
:伝統構法の建物は、変形性能を考慮すると少ない耐震要素であっても大地震にも耐えることが出来る。しかし、変形が大きくなり固有周期が大きくなることが条件なので、大地震時は建物の変形が大きく、地震には耐えるが、仕上げなどの損傷が起こることは受け入れなければならない。
■建物の変形が進むと建物の剛性(K)が小さくなる
建物の剛性 K=Q(耐力)/σ(変位)
■建物の剛性が小さくなると固有周期(T)が大きくなる
建物の固有周期 T=2π√M/K M:質量
■地震により建物にかかる力は建物の重量に地震による加速度をかけたもの
Qn(地震力)=M(質量)×Sa(加速度)
■建物の重さが一定であれば建物にかかる地震力は地盤から建物が受ける加速度の大きさで決まる
S0:工学的基板上の加速度応答スペクトル
Gs:表層地盤による加速度の増幅率
■まとめ
:建物は地震による力を受けると損傷する
:建物が損傷すると変形し、剛性が低下する
:剛性が低下すると建物の固有周期が長くなる
:固有周期が長くなると建物に入力される加速度は小さくなる
:建物は振動を繰り返すことにより加速度は減衰する
:建物に入力する加速度が小さくなると建物が受ける地震力が小さくなる
:建物の耐力が変形しても落ちなければ、地震力より建物耐力が大きくなる地点がある
:その時の変形が建物の応答値であり、その変形角が伝統構法のように変形能力がある耐震要素で作られている場合、1/15より小さければ建物は倒壊しないと判断する。
:建物の倒壊を防ぐには、建物の加重を減らすことが効果的
耐震性能評価計算法(限界耐力計算法)木造
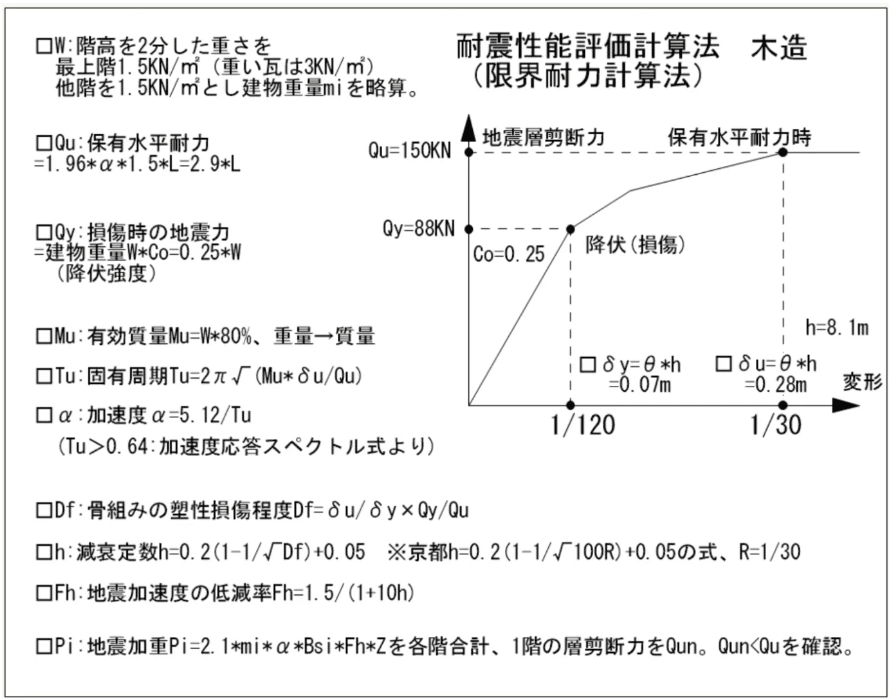
①■地震力算定用の建物荷重W:階高を2分した重さを全階とも1.5KN/㎡とする。(重い瓦の場合は最上階を3KN/㎡)W=350KN
3F(30㎡),2F(50㎡),1F(70㎡)の場合、R階:1.5×30㎡=45≒50KN、3階:1.5×30㎡+1.5×50㎡=120KN、2階:1.5×50㎡+1.5×70㎡=180KN
②■これ以上耐力が上がらない 保有水平耐力Qu=2.9×α×L:(金物損傷、めりこみ)
Qu=1.96×(α:壁倍率)×(1.5:終局耐力までの余裕)×(L:耐力壁の総長さ)
X方向、壁倍率α=4、耐力壁l=13mの時、2.9×4×13=150、Qu=150KN
Y方向、壁倍率α=4、耐力壁l=15mの時、2.9×4×15=170、Qu=170KN
□保有水平耐力時、層間変形角θ=1/30と変位δu=h/30
木造住宅の大地震時の層間変形角θ=1/30と設定する。(C0=0.25と仮定) θ=δ/hなので、δ=θh→δu=h/30
軒高h=8.4mの時、δ=8.4/30、δu=0.28m
※木造建築物の安全限界変位を1/15に設定した場合(C0=0.25~0.3程度必要)、大地震時の損傷(大破)が10%に収まる(京都の考え方)
□保有水平耐力時、固有周期Tu=2π√(Mu・δu/Qu)
多質点系を1質点系に置換する。1質点系の有効質量Mu=建物重量×80%とする。尚、質量表示に変換(KN→t)
有効質量Mu=350×80%=280KN、更に質量に変換 280KN→Mu=28t
Tu=2×3.14×√(28×0.28/150)=1.4秒、Tu=1.4秒
③■骨組損傷開始時の降伏強度 地震力Qy=建物重量W×Co
Co=0.25(250gal)程度で骨組みが損傷(降伏)すると仮定。標準剪断力係数Co=0.25=地震力Qy/建物重量W
Qy=350×0.25=88、Qy=88KNで損傷が始まる。
□損傷開始時、層間変形角θ=1/120と変位δy
木造住宅の降伏強度Qyでの損傷時の層間変形角θ=1/120とする。(C0=0.25と仮定) θ=δ/hなので、δ=θh→δy=h/120
軒高h=8.4mの時、δ=8.4/120、δy=0.07m
④■地震加速度の低減率Fh=1.5/(1+10h)
地震エネルギーの吸収効果は、損傷程度Df、及び減衰定数hから求められる、地震加速度の低減率Fhとして評価される。
□骨組みの塑性損傷程度Df=δu/δy×Qy/Qu
X方向、Df=0.28/0.07×88/150≒2.3、Df≒2.3
Y方向、Df=0.28/0.07×88/170≒2.1、Df≒2.1
□減衰定数h=0.2(1-1/√Df)+0.05(木造は強度にばらつきがあるので0.2とする)
X方向、h=0.2(1-1/√2.3)+0.05≒0.12、h≒0.12
Y方向、h=0.2(1-1/√2.1)+0.05≒0.11、h≒0.11
→低減率Fh=1.5/(1+10h)
X方向、Fh=1.5/(1+10×0.12)=0.68、Fh=0.68(68%)←これが知りたかった!
Y方向、Fh=1.5/(1+10×0.11)=0.71、Fh=0.71(71%)←これが知りたかった!
※京都の町並み(hを一発で出す方法)
h=0.2(1-1/√100R)+0.05の式。R=1/30とすれば、h=0.14となり、Fh=1.5/(1+10×0.14)=1.5/2.4=0.63、Fh=0.63(63%)
⑤■大地震時に骨組みに作用する地震加重Pi=Gs×mi(質量)×α×Bsi×Fh×Z
(Bsiは、R階1.0、3階0.8、2階0.6とする)
□地震加速度応答スペクトルを用い、建物周期Tuより応答加速度αを算出。
Tu<0.16秒の時、加速度α=(3.2+30Tu)、0.16秒<Tu<0.64秒の時、加速度α=8m/s2、0.64秒<Tuの時、加速度α=5.12/Tu
Tu=1.4秒>0.64秒なので、α=5.12/1.4=3.66、α=3.66m/s2
□表層地盤による加速度増幅率Gsを2.1倍とする。(2種地盤で1.5~2.025)
X方向、R階:PR=2.1×5t×3.66m/s2×1.0×0.68×1=26.13、PR≒27KN
Y方向、R階:PR=2.1×5t×3.66m/s2×1.0×0.71×1=27.29、PR≒28KN
X方向、3階:P3=2.1×12t×3.66m/s2×0.8×0.68×1=50.17、P3≒51KN
Y方向、3階:P3=2.1×12t×3.66m/s2×0.8×0.71×1=52.38、P3≒53KN
X方向、2階:P2=2.1×18t×3.66m/s2×0.6×0.68×1=56.44、P2≒57KN
Y方向、2階:P2=2.1×18t×3.66m/s2×0.6×0.71×1=58.90、P2≒59KN
⑥■必要保有水平耐力Qun(1階の層剪断力をQunとする)
大地震時の水平荷重によって各層には層剪断力が生じる。その層剪断力Qiにつり合う剪断耐力が必要保有水平耐力Qunである。
X方向、1階の層剪断力Qun=27+51+57=135、Qun=135KN
Y方向、1階の層剪断力Qun=28+53+59=140、Qun=140KN
※有効質量Mu用い、Qunを一発で出す方法。Mu=0.8Mall=28t、α=5.12/Tu=5.12/1.4=3.66m/s2、Fh=0.68。Qun=2.1×Mu×α×Fh=2.1×28t×3.66×0.68=146KN
⑦■必要値Qun<保有値Qnの確認
X方向、必要値Qun=135KN<保有値Qu=150KN OK!
Y方向、必要値Qun=140KN<保有値Qu=170KN OK!
いいなと思ったら応援しよう!

