
【Pythonで統計モデル】SEM5:多変量回帰分析
はじめに
こんにちは、GAテクノロジーズAISCの王です。
この記事はPythonで統計モデル(SEM編)の続きであり、構造方程式モデリング(SEM:Structural Equation Modeling)をPythonでどこまで実行できるかを調査・確認することを目的にしています。
一般的にSEMの研究においては、Rが主流のツールですが、今年は私たちのデータサイエンスチームが定期的に学習セッションを開催し、SEMの知識を学びながら、Rの計算プロセスをPythonで再現しようとしています。現時点で、私たちは以下の4回のセッションを実施しました。
【Pythonで統計モデル】SEM1:速習・構造方程式モデリング|福中公輔
【Pythonで統計モデル】SEM2:母数に関する制約|福中公輔
【Pythonで統計モデル】SEM3:パス解析(逐次モデル)|白圡義泰
【Pythonで統計モデル】SEM4:パス解析(非逐次モデル)|Masayoshi Mita
今回の記録はこのシリーズの第5回目です。多変量回帰分析についての主要な内容を紹介します。
この「Pythonで統計モデル」の記事シリーズでは今後も各メンバーが学んだことをそれぞれ記事にしていきます。もしご興味のある方がいらっしゃいましたら、AISCのマガジンのフォローをお願いします!
なお、私はSEMについては全くの初学者になります。もし誤りなどがあればコメントでご教示いただけますと幸いです。
教科書
本記事で参考にした教科書は、豊田秀樹先生によって2014年に出版された『共分散構造分析[R編]―構造方程式モデリング―』です。使用したデータは東京図書のウェブサイトからダウンロードできます。
操作環境
本記事で使用した操作環境は以下の通りです:
OS:MacOS 12.6、Python 3.9.6
また、必要なパッケージは以下の通りです。すでにインストールされている場合は省略してください。
# packageのインストール
pip install numpy pandas
pip install graphviz
pip install semopy
pip install pingouinなおsemopyは構造方程式モデリング(SEM )を行うためのパッケージで、ドキュメントは以下にあります。
本記事ではここから重要な部分をいくつかピックアップしてご紹介します。網羅的な解説はしませんので、適宜、必要に応じてご参照ください。
多変量回帰分析
多変量回帰分析(Multivariate Regression Analysis)とは、複数の従属変数を複数の独立変数で予測するモデルのことです。私は学生時代に重回帰分析を使いましたが、重回帰分析(Multiple Regression Analysis)と多変量回帰分析はいずれも統計的な手法で、複数の説明変数を使用して目的変数をモデル化し解析する点で共通しています。ただし、これらの手法には重要な違いがあります。
重回帰分析:1つの目的変数に対して複数の説明変数を使用します。つまり、単一の目的変数に対する回帰分析です。たとえば、家賃(目的変数)を広さや立地などの要因(説明変数)で説明する場合、重回帰分析を使用できます。
多変量回帰分析:複数の目的変数(通常は2つ以上)に対して複数の説明変数を使用します。複数の目的変数に対する回帰分析ができます。たとえば、家賃、部屋の広さ、および周辺の犯罪率(複数の目的変数)を同時に説明する場合、多変量回帰分析を使用できます。より複雑なモデルであり、複数の目的変数間の相関を考慮に入れ、同時に複数の説明変数の効果を評価できる。
目的変数ごとに重回帰分析をN回繰り返すと、多変量回帰にならないかと思っている方もいるかもしれませんが、実は目的変数間の相関を仮定できるかどうかは重要な相違点です。
重回帰分析だと目的変数間の相関を仮定できない一方、多変量回帰モデルを適用することでそれができるようになるというのがメリットになります。
つまり、多変量回帰分析を使ってモデリングすることで目的変数間の偏相関が求められるようになるということです。
多変量回帰分析による偏相関
import pandas as pd
import semopy
import graphviz
import pingouin as pg
stats = pd.read_csv('dat/stats.csv',encoding="Shift-JIS",index_col=0)
stats.head(5)今回使用するのは「都道府県別の架空データ」で、項目として「x(交通事故数)」「y(病院数)」「z(人口(千人))」が含まれています。
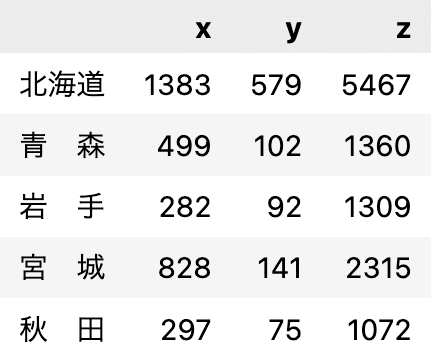
「人口z」の影響を取り除くと、「事故x」と「病院y」との間には、相関がほとんどない結果になります。
partial_corr = pg.partial_corr(data=stats, x='x', y='y', covar='z')
print("相関係数:",round(stats['x'].corr(stats['y']),3))
print("偏相関係数:", round(partial_corr['r'].values[0],3))
相関係数: 0.648
偏相関係数: 0.097教科書では偏相関係数を計算する時に、すべての変数間の相関係数を小数点第4位で丸めてから計算したので、偏相関係数が少しずれています。
# 偏相関係数: 人口の影響を除く
r = stats.corr().round(3) # ここで丸めないと書籍と合わない
r_xyz = (r.loc["x", "y"] - r.loc["x", "z"] * r.loc["y", "z"]) / np.sqrt( (1 - r.loc["x", "z"]**2) * (1 - r.loc["y", "z"]**2) )
round(r_xyz, 3)
0.098偏相関係数を確認した後に、早速に多変量回帰分析を行いましょう!
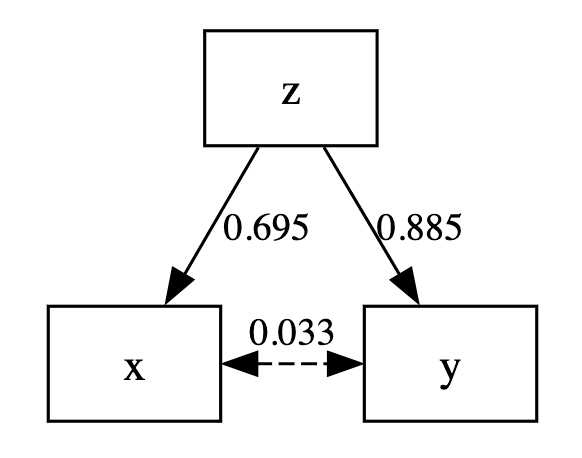
「人口z」を説明変数、「事故x」と「病院y」を目的変数として構造方程式モデリングで分析をすると、
mod = """
x ~ z
y ~ z
y ~~ x
z ~~ z
"""
# 分析の実行
stats_std = stats.apply(lambda x: (x-x.mean())/x.std(ddof=0), axis=0) # 標準化
model = semopy.Model(mod)
result = model.fit(data=stats_std, axis=0), obj='MLW')
inspect = semopy.Model.inspect(model,std_est=True)
print(inspect.round(3))分析結果は `inspect()` で出力することができます。 Est. Stdの列が標準化解になります。
lval op rval Estimate Est. Std Std. Err z-value p-value
0 x ~ z 0.695 0.695 0.105 6.623 0.000
1 y ~ z 0.885 0.885 0.068 13.036 0.000
2 z ~~ z 1.000 1.000 0.206 4.848 0.000
3 y ~~ x 0.033 0.033 0.049 0.665 0.506
4 y ~~ y 0.217 0.217 0.045 4.848 0.000
5 x ~~ x 0.517 0.517 0.107 4.848 0.000なんとxyの偏相関係数は0.033になり、0.097とずれました。
でも先ほどはモデルにfitする時に、標準化したデータを使いましたので、今度は素データのままでモデルを実行してみます。するとどうなるでしょう?
lval op rval Estimate Est. Std Std. Err z-value p-value
0 x ~ z 0.248 0.701 0.037 6.736 0.0
1 y ~ z 0.047 0.781 0.006 8.581 0.0
2 z ~~ z 6791458.941 1.000 1400971.009 4.848 0.0
3 y ~~ x 0.000 0.000 9446.576 0.000 1.0
4 y ~~ y 9665.124 0.390 1993.763 4.848 0.0
5 x ~~ x 433949.572 0.509 89516.962 4.848 0.0こちらもダメです!しかも偏相関係数は0になりました。
ちなみに同じデータを使って、Rでも一度実行しました。コードと出力結果は以下になります。
> data3_1 <- read.csv("dat/stats.csv", row.names = 1, fileEncoding = "Shift-JIS")
> model3_1 <- ' x ~ z
+ y ~ z'
> fit3_1 <- sem(model3_1,data = data3_1)
> summary(fit3_1,standardized=T,fit.measures=T)
#出力した結果
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
x ~
z 0.248 0.038 6.623 0.000 0.248 0.695
y ~
z 0.047 0.004 13.036 0.000 0.047 0.885
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.x ~~
.y 4223.023 6354.573 0.665 0.506 4223.023 0.097
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.x 448909.269 92602.911 4.848 0.000 448909.269 0.517
.y 4188.050 863.929 4.848 0.000 4188.050 0.217結論を言うと、Rの結果(xとyのStd.all)は偏相関係数と一致しました!でもsemopyで実行する場合、素データと標準化データを問わず、xとyの標準化解が全部ずれました。
ズレる原因を軽く調査
semopyの計算法
まずsemopyのソースコードを見てみましょう!
semopyの標準化解を出したい場合は、inspect()関数に‘std_est=True’のoptionをつける。その時に実行されたのは以下の計算です
if std_est:
sigma, (_, c) = model.calc_sigma()
w_cov = c @ model.mx_psi @ c.T
stds = np.sqrt(w_cov.diagonal())
std_full = np.sqrt(sigma.diagonal())stds = np.sqrt(w_cov.diagonal())は観測変数の共分散行列 (w_cov) の対角成分(共分散の分散成分)を取得し、その平方根を計算して、各観測変数の標準偏差を求めます。これにより、各観測変数の標準偏差が計算されます。
std_full = np.sqrt(sigma.diagonal()):はシグマ行列 (sigma) の対角成分を取得し、その平方根を計算して、標準偏差を求めます。これにより、モデル全体の標準偏差が計算されます。
最後に`stds`と`std_full`で割って、標準化解を出す仕組みです。
そうしてシグマの計算コードを探し出してみると、普通に構造化された共分散を推定している式でした。
def calc_sigma(self):
beta, lamb, psi, theta = self.matrices[:4]
c = np.linalg.inv(self.identity_c - beta)
m = lamb @ c
return m @ psi @ m.T + theta, (m, c)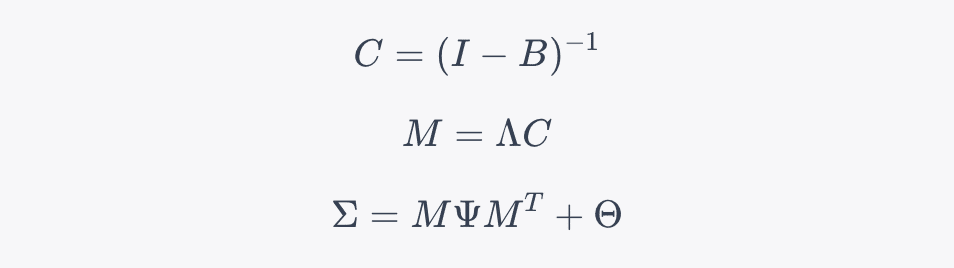
Rの計算法
lavvanのソースコードも見てみました。Std.allはlav_standardize_allという関数によって計算されていますが、私はRに関して詳しくないので、詳細までは読み取れませんでした。
最後に
多変量回帰分析は独立変数や従属変数の数に制限がなく、さまざまなモデルに適用でき、また偏相関の計算にも活用できる非常に柔軟な手法です。semopyを使用した今回の計算では、Rの計算過程を完全に再現することはできませんでしたが、ChatGPTを活用することで問題の一部の原因を推測しました。
両方の演算方には違いがありませんが、Pythonでの行列計算はすべてNumPy経由で、lavaanは自分の関数を利用しています。その過程で数値の精度や計算方法に微妙な違いが生じる可能性があります。この違いが、PythonのsemopyとRのlavaanで標準化解が異なる理由の一部かもしれません。
したがって、PythonとRで異なる結果が得られる場合、その違いは計算の実装や数値計算ライブラリの違いに起因している可能性があることを考慮に入れるべきです。また、標準化データからの計算結果と素データからの標準化解が違う事によって、データの前処理やモデルの仕様も結果に影響を与える可能性があるため、注意が必要です。
今後の流れ
本記事シリーズでは今後もPythonでSEMを実行していきます。次回は白圡さんがMIMICモデルを紹介する予定です。ご興味のある方はぜひAISCのマガジンのフォローをお願いします!
