「波」を掛けるということ

仕事から帰りながら、いつものように波のことを考えていました。

正弦波は波の中で一番ノーマルな奴、つまり並の波です。
そんなやつを掛け算する程度の演算簡単だよなと思っていました。

しかしふと、自分の中に2つの矛盾する常識があることに気が付いたのです。

常識①「正弦波を掛けると、その分だけ周波数が高くなるのだから、形が横に”縮む”」

常識②「正弦波を掛けると、その周波数の正弦波だけど、ガワに元の形が現れる」

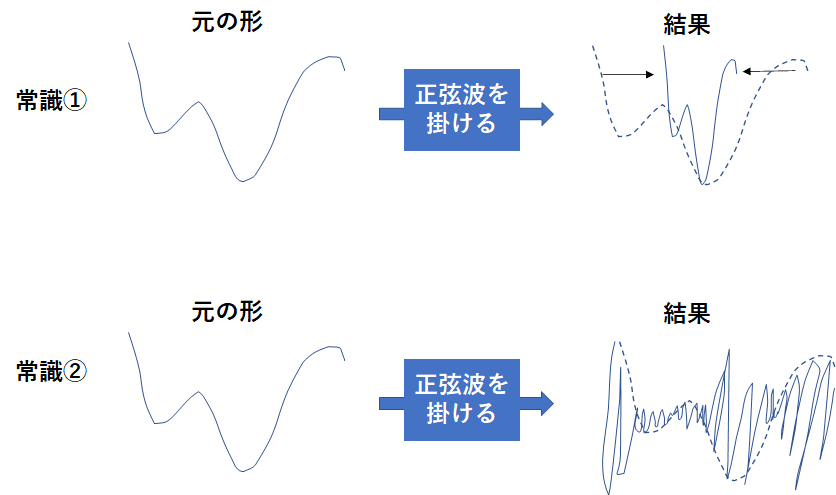
・・・どっちも知ってる。あれ？なんだ？と思ったわけです。

常識①について

結論から言うと、合ってるっぽいです。フーリエ変換を知っている方ならば、「正弦波を乗算すると、周波数の世界では横にスライドする」ことを知っているはず。ちゃんとした数式・証明はこちらを参照ください

正弦波は複素数の世界で扱うと等速円運動の実軸写像として考えられるのでよく複素数の形で表現されます（e^jwt）。角速度w(rad/s)で反時計回りにぐるぐる回っている影を見る（Realパートを見る）と正弦波(coswt)になるんですね。上の図のように、周波数軸で形を保ったまま上の方向に行くってことは、時間軸上の波形が縮むってこと。このイメージがない人は、この説明やと結局縮む理由が分からん気がします。音声2倍速早送り加工とかは、時間軸で縮めるイメージあると思うんですけど、声がコロ助みたいに高くなるじゃないですか。あれがまさに上の図です。

違う説明をすると、

これが成り立つからですね。これならわかる人増えるかも？形が変わる前の関数を正弦波で限定しちゃいましたが。関数はすべて正弦波の足し算で表現できるんで(結局フーリエ変換の前提が…)、これが成り立てば上も成り立ちます。

ちなみに性質知らなくてもオイラーの公式と加法定理使えば簡単に導出できます。

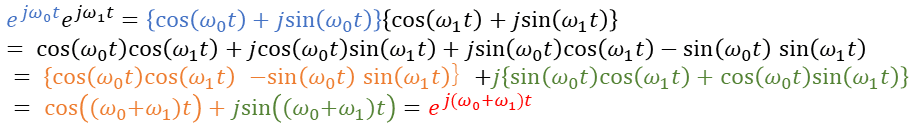
色付けで逆にごちゃごちゃするあるある

常識②について

あれ？じゃあ2個目が間違ってたんかと。

No。あってます。適当にエクセルでかけてみた結果が以下。

ガワのことを包絡線というのですが、結果の包絡線がちゃんと元の形してます。でも、常識①的には、cos(11wt)になってほしいところですよね。

仕方がないので、こっちでやった計算上でやった考え方に当てはめてみましょう。

実は、さっきエクセルでやったのはe^jwtではなくてcoswtを掛けたという操作です。cosを掛けると、項が2つあるので、全体が1/2になってプラマイに同じだけ周波数がずれて分身します。

つまり、coswtにcos10wtを掛けたらcos11wtではなく、1/2(cos11wt+cos9wt)になるんです。(-9wtだけどコサインは偶関数なのでマイナス消しちゃった)

色合いがきもいですがちゃんと一致しました(青線は1/2かけてます)。なんだか感動。

結論

はい。つまり、常識①は複素数の世界の正弦波e^jwtを掛けた時に起きる現象で、常識②は実数の世界の正弦波coswtを掛けた時に起こる現象なんですね。

同じようなもんだろって思ってたんではぇ～～って思いました。

余談(本題)

さて、そもそもなぜ上の2つの常識があったのかというと通信関連の知識からでした。①のほうはFMラジオに使われている周波数変調、②のほうはAMラジオに使われている振幅変調という技術の説明ほぼそのままなんですね。

出発点はそこだったんですが、②の方の結論をみてん？と思いました。

「うなり」だ！

ほとんど同じ高さの音を2つ同時に出すと、そのズレが少しでもあると大きさがグワングワンなるってやつです。

真ん中のラが440Hzのピアノと、宗教上の理由で442Hzに調律されたピアノがあるとします。

それを同時にならすと、1秒間に2回(442-440=2Hz)の速さでビブラートがかかります。

何故かというと、さっきの逆です。440Hzの正弦波と442Hzの正弦波を足すと、441Hzの正弦波で、包絡線が1Hzの正弦波になっているってことです。

比較の仕方がアホかつ色がきもいですが参考までに一致しました(足し算の方は1/2かけてます)。ちなみに1Hzより細かい包絡線の周波数が見えるのは横軸のプロット点数がサンプリング定理を満たしてないからです。

あれ、なんでうなりは2Hzなのに1Hz？と思ったのですが、包絡線は上の図のように正弦波の一周期に2回ウワンって振幅が大きくなります。なので、倍の周波数に聞こえるようです。

＃まあ、積和の公式で分かることなんですけどね。

さいごに

なんだか授業チックになっちゃいましたが、備忘録として。(どっか間違ってるかもしれませんが)これを見て同じように疑問を感じて、同じように納得いただけたら幸いです。