Stage3 深層学習Day1

1.ニューラルネットワークの全体像

1-1.ニューラルネットワークの全体像

1-2.ニューラルネットワークでできること

・回帰
連続する実数値をとる関数の近似

【主な手法】
　　　・線形回帰
　　　・回帰木
　　　・ランダムフォレスト
　　　・ニューラルネットワーク（NN）

・分類
性別（男あるいは女）や動物の種類など離散的な結果を予想するための分析

　【主な手法】
　　・ベイズ分類
　　・ロジスティック回帰
　　・決定木
　　・ランダムフォレスト
　　・ニューラルネットワーク(NN)

2.入力層〜中間層

2-1.入力層から中間層

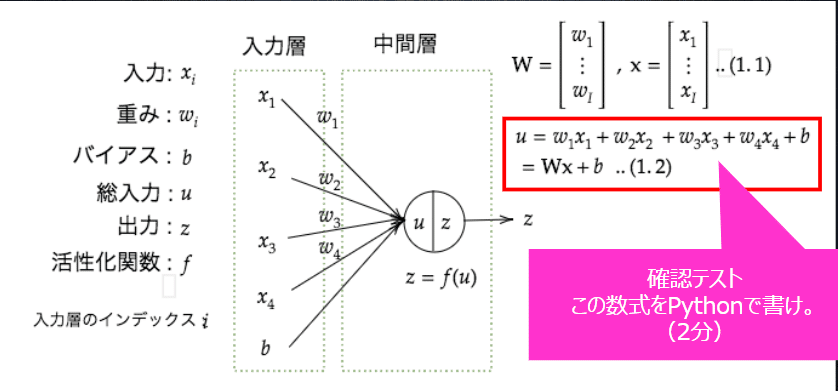
＜確認テスト＞

上図にある、計算式をpythonで書け。

＜回答＞

u1 = np.dot(x, W1) + b1

2-2.活性化関数

ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数。入力値の値によって、次の層への信号のON/OFFや強弱を定める働きをもつ

＜確認テスト＞

線形の図と、非線形の図を描き、簡単に説明せよ

＜回答＞

・線形な関数：y=axのように直線で表されるような関数（オレンジ字）
・非線形な関数：直線で表せず、曲線で表されるような関数（緑字）

2-3.中間層の活性化関数

・ステップ関数

しきい値を超えたら発火する関数であり、出力は常に１か０。パーセプトロン（ニューラルネットワークの前身）で利用された関数。課題としては、０-1の間を表現できず、線形分離可能なものしか学習できなかった。　

・シグモイド関数

０〜１の間に緩やかに変化する関数で、ステップ関数ではON/OFFしかない状態に対し、信号の強弱をつけられるようになり、予想ニューラルネットワークの普及のきっかけとなった。課題としては、大きな値では出力の変化が微小なため、勾配消失問題を引き起こす事があった。

・RELU関数

今最も使われている活性化関数。勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。

＜確認テスト＞

配布されたソースコードより、z=f(u)に該当する箇所を抜きだせ

＜回答＞

z1 = functions.sigmoid(u)

3.出力層

3-1.誤差関数

出力層の結果と訓練データ（正解値）との比較を行い、どれほどの誤差が出たかを確認する。

＜確認テスト＞

二乗誤差ではなぜ引き算ではなく二乗するかを述べよ。また1/2はどういう意味を持つか述べよ。

＜回答＞

誤差に負の値が出てくる場合も誤差の計算ができるようにするため。また、この後に微分をした際に発生する値と相殺することができる。

3-2.出力層の活性化関数

・中間層と出力層の違い
【値の強弱】
中間層：しきい値の前後で信号の強弱を調整
出力層：信号の大きさ（比率）をそのままに変換
　
【確率出力】
分類問題の場合、出力層の出力は０〜１の範囲に限定し、総和を1にする必要がある。
→中間層と出力層では利用される活性化関数が異なってくる。

＜確認テスト＞

ソフトマックス関数のソースコードを配布データから抜き出し、1行ずつ説明せよ。

＜回答＞

def softmax(x):
   if x.ndim == 2:
       x = x.T
       x = x - np.max(x, axis=0)
       y = np.exp(x) / np.sum(np.exp(x), axis=0)
       return y.T
 #指数関数の値が大きな値になったときのオーバーフロー対策
   x = x - np.max(x) 
 #実際の計算は以下
   return np.exp(x) / np.sum(np.exp(x))

＜確認テスト＞

交差エントロピーのソースコードを配布データから抜き出し、1行ずつ説明せよ。

＜回答＞

  def cross_entropy_error(d, y):
   if y.ndim == 1:
       d = d.reshape(1, d.size)
       y = y.reshape(1, y.size)
   # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
   if d.size == y.size:
       d = d.argmax(axis=1)
   batch_size = y.shape[0]
   #実際の計算は以下
   #1e-7は、分母が0のときに計算ができるようにする目的
   return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size

4 勾配降下法

4-1.勾配降下法

深層学習の目的：学習を通して誤差を最小にするネットワークを作成すること
→　誤差E(w)を最小とするようなパラメータwを発見すること
→　勾配降下法を利用して、パラメータを最適化

＜確認テスト＞

上の数式に該当するソースコードを探せ

＜回答＞

network[key]  -= learning_rate * grad[key]
grad = backward(x, d, z1, y)

「ε」は学習率。学習率が大きすぎると収束せずに発散してしまうが、小さすぎると収束まで時間がかかってしまう。

勾配降下法の学習率の決定、収束性向上のためのアルゴリズムには以下のようなものがある。

　　・Momentum
　　・AdaGrad
　　・Adadelta
　　・Adam

4-2.確率的勾配降下法

確率的勾配降下法のメリットは以下の通り。

　　・データが冗長な場合の計算コストを軽減
　　・望まない局所極小解に収束するリスクを軽減
　　・オンライン学習ができる

＜確認テスト＞

オンライン学習とは何か2行で説明せよ

＜回答＞

オンライン学習とは学習データが入ってくるたびにその都度、新たに入ってきたデータのみを使って学習を行う。

4-3.ミニバッチ勾配降下法

ミニバッチ勾配降下法のメリットは、確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効利用できるという点。
　→　CPUを利用したスレッド並列化やGPUを利用した、SIMD並列化

＜確認テスト＞

＜回答＞

5. 誤差逆伝播法

算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播。
最小限の計算で、各パラメータでの微分値を解析的に計算する手法。

計算結果（=誤差）から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる。

＜確認テスト＞

誤差逆伝播法では不要な再帰的処理を避ける事が出来る。既に行った計算結果を保持しているソースコードを抽出せよ。

＜回答＞

delta2 = functions.d_mean_squared_error(d, y)

＜確認テスト＞

＜回答＞

delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
grad['W1'] = np.dot(x. T, delta1)