Stage3 深層学習Day2

勾配消失問題、学習率最適化手法、過学習、畳み込みニューラルネットワークについてまとめる。

1 勾配消失問題

誤差逆伝播法が下位層に進んでいくに連れて、勾配がどんどん緩やかになっていく。そのため、勾配降下法による、更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。

勾配消失問題を回避する手法は、主に活性化関数の変更、初期値の設定方法の工夫、バッチ正規化の3つである。

1-1 活性化関数

シグモイド関数ではなく、ReLU関数を使用することで勾配消失問題を回避できる。

1-2 初期値の設定方法

・Xavier（ザビエル）

重みの要素を、前の層のノード数の平方根で除算した値で初期値を設定する。活性化関数にはReLU関数、シグモイド（ロジスティック）関数、双曲線正接関数を使用する。

・He

重みの要素を、前の層のノード数の平方根で除算した値に対し√２をかけ合わせた値で初期値を設定する。活性化関数にはReLU関数を使用する。

＜確認テスト＞

重みの初期値に0を設定すると、どのような問題が発生するか。

＜回答＞

すべての次に伝播する値が同じ値で伝わるため、パラメータチューニング行われなくなる。

1-3 バッチ正規化

ミニバッチ単位で、入力値のデータの偏りを抑制する手法。

＜確認テスト＞

一般的に考えられるバッチ正規化の効果を2点挙げよ。

＜回答＞

・計算が高速化する

・勾配消失問題を防ぐことができる

1-4 実装

活性化関数と初期値の設定方法の組み合わせで勾配消失が発生するかを実験する。

・シグモイド関数 - ガウス初期化

学習が進まない。

・ReLU関数 - ガウス初期化

急激に学習が進んだ。

・シグモイド関数 - Xavier初期化

初期から学習が進んでいる。

・ReLU関数 - He

急速に学習が進む。

・バッチ正規化

勾配消失を防げている。

2 学習最適化手法

学習率は大きすぎると発散してしまうことがあり、小さすぎると収束まで時間がかかってしまう。そのための学習率の最適化手法をまとめる。※確認テストの回答も兼ねる。

2-1 モメンタム

誤差をパラメータで微分したものと学習率の積を減算した後、現在の重みに前回の重みを減算した値と慣性の積を加算する。局所的最適解にならず、大域的最適解となる。谷間についてから最も低い位置(最適値)にいくまでの時間が早い

2-2 AdaGrad

誤差をパラメータで微分したものと再定義した学習率の積を減算する。勾配の緩やかな斜面に対して、最適値に近づける。

2-3 RMSProp

誤差をパラメータで微分したものと再定義した学習率の積を減算する。局所的最適解にはならず、大域的最適解となる。また、ハイパーパラメータの調整が必要な場合が少ない。

2-4 Adam

モメンタムの過去の勾配の指数関数的減衰平均、RMSPropの過去の勾配の2乗の指数関数的減衰平均、の2点をそれぞれ孕んだ最適化アルゴリズムである。モメンタムおよびRMSPropのメリットを孕んだアルゴリズムである。

2-5 実装

いくつかの学習最適化手法を実行し、学習結果を確認する。

・モメンタム

徐々に学習が進んでいる。

・AdaGrad

・RMSProp

よく学習が進んでいる。若干が学習気味。

・Adam

学習も順調に進み、過学習も発生していない。

3 過学習

過学習とは、ネットワークの自由度が高いことが原因で、テスト誤差と訓練誤差とで学習曲線が乖離すること。

3-1 正則化

誤差に対して、正則化項を加算することで、重みを抑制する。過学習がおこりそうな重みの大きさ以下で重みをコントロールし、かつ重みの大きさにばらつきを出す。

正則化には、L1正則化とL2正則化がある。

＜確認テスト＞

機械学習の線形モデルの正則化はモデルの重みを制限することで可能になる。線形モデルの正則化手法の中にリッジ回帰という手法がある、その特徴は何か？

＜回答＞

ハイパーパラメータを大きな値に設定すると、すべての重みが限りなく0に近づく。

＜確認テスト＞

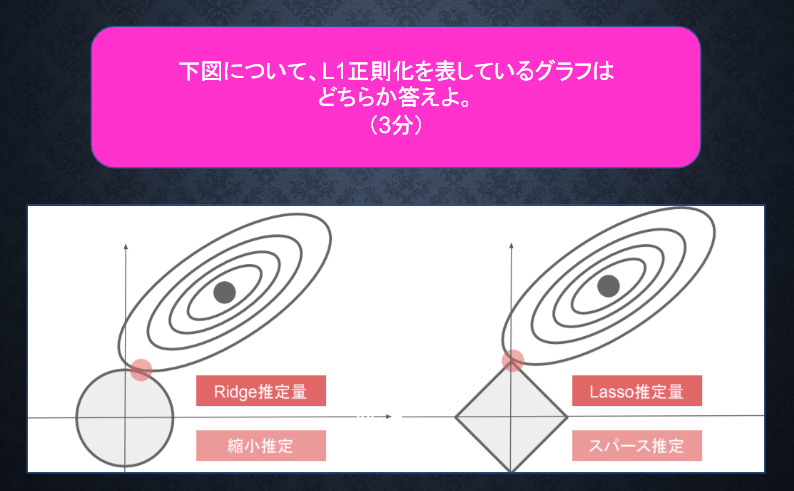
＜回答＞

L1正則化は右の図。左の図はL2正則化。

3-2 ドロップアウト

ランダムにノードを削除して学習させること。データ量を変化させずに、異なるモデルを学習させていると解釈できる。

3-3 実装

過学習を発生させる。

訓練データとテストデータに対する正解率が大きく乖離しており、過学習が発生していると言える。

・L2正則化

若干過学習が解消している。

・L1正則化

学習が進んでいない。

・ドロップアウト

過学習は残存している。

4 畳み込みニューラルネットワーク

画像認識の分野で活躍。音声データのような時系列データも加工により活用可能。畳み込み層、プーリング層という概念が登場する。

以下が全体像。

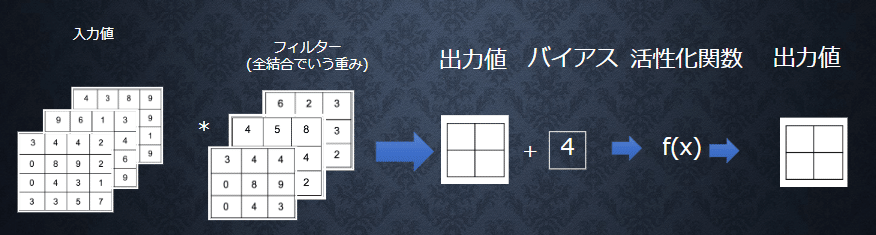
4-1 畳み込み層

畳み込み層では、画像の場合、縦、横、チャンネルの3次元のデータをそのまま学習し、次に伝えることができる。3次元の空間情報も学習できるような層が畳み込み層である。

4-1-1 バイアス

全ての値に一律加える値。

4-1-2 パディング

出力画像のサイズを調整するため、入力画像に固定のデータを追加する。

4-1-3 ストライド

フィルター演算する際にずらすマス目の数。

4-1-4 チャンネル

階層。その階層の分だけフィルターが必要。

4-2 プーリング層

Max値を取ることをマックスプーリング、平均値を取ることをアベレージプーリングと呼ぶ。

＜確認テスト＞

サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なおストライドとパディングは1とする。

＜回答＞

7×7

OH(Output High)
=H(hight)+2P(padding)-FH(FilterのHight)/S(ストライド)+1
=(6+2×1-2)/1+1
=7

OW(Output Width)
=W(Width)+2p(padding)-FWidth(FilterのWidth)/S(ストライド)+1
=(6+2×1-2)/1
=7

4-3 実装

conv - relu - conv - relu - pool - affine - relu - affine - softmax という畳み込み層を2層持つCNNを実装。

5 最新のCNN

5-1 AlexNet

2012年に登場した、トロント大学が開発したネットワーク。畳み込み層5層にプーリング層でできており、従来のモデルに比べると深い層構造になっていた。また、サイズ4096の全結合層の出力にドロップアウトを使用することで過学習を防いでいた。