トロピカルな計算練習(16)
ずいぶん時間があいてしまいました。生きていますよ。
前回はニュートン図形を導入しまして、トロピカルカーブとの対応があることを見ました。
今回はこのニュートン図形で遊びましょうという回です。
遊ぶだけですから大して進展はありません。
ニュートン図形の興味というと、まず何パターンあるか考えるのが楽しそうです。
しかしながら一般次元はなかなか考えにくい。
ひとまず二次までを見てみようと思います。
しかし、それでもまだ大変なので、最初に対称な図形を見ることにします。
つまり、
$$
ax^2+ay^2+bxy+cx+cy+d
$$
この形を見るということです。


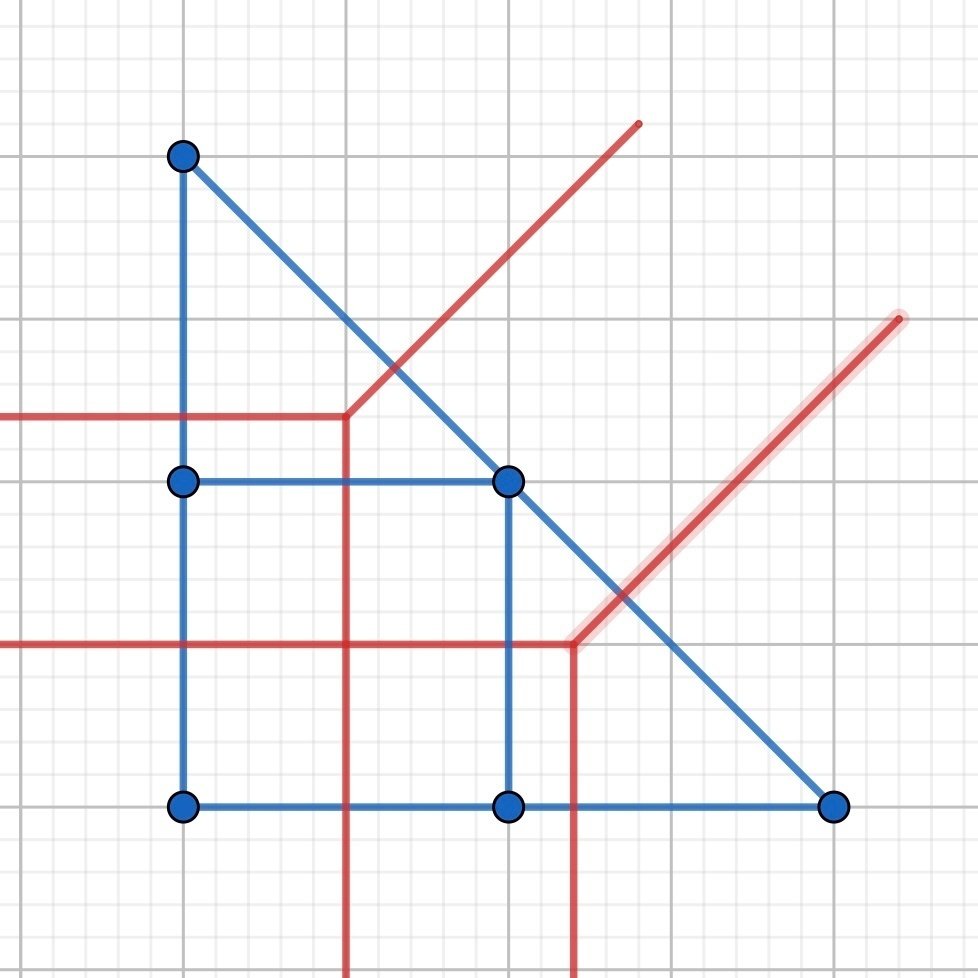



以上、この6つのはずです。
非対称な場合はどうかというと、$${y=x}$$での対称性を加味して、$${7\times2}$$パターンあります。







若干トロピカルカーブの書き方でズルをしてますが、状況によっては垂線がうまく書けないので、三角形の外に垂線がはみ出しても良いこととしています。
ひとまず以上で二次式のニュートン図形は取り尽くしたかなと思いますので次行きましょう。
三次式の場合はちょっとやそっとじゃできません。
私は対称な図形でさえ投げ出しました。
じゃあこの記事では何をするかというと、トロピカルカーブが対称でかつ"穴"をもつ場合を考えます。

このように、最も外側の三角形$${(n,0),(0,n),(0,0)}$$の内部に点が存在しないとトロピカルカーブに"穴"を作ることはできません。
二次式ですと、全ての頂点が三角形$${(n,0),(0,n),(0,0)}$$の辺上に存在します。
そのため、トロピカルカーブに"穴"が生じるのは三次以上ということができます。

で、どうすれば"穴"ができるのかというと、3次式でいえば$${axy}$$の項を調整して$${(1,1)}$$の点に線が通るようにすれば良いわけです。

これは先ほどの"穴"ありトロピカルカーブの図から$${(1,1)}$$の点を調整してニュートン多面体の折れ線(青)が$${(1,1)}$$を通らないようにした図形です。
(ちょっと図が分かりにくいですが、赤線はトロピカルカーブなので、こいつは$${(1,1)}$$を通っても別に良いのです)
そうするとつまり、僕らが今調べたい「対称かつ穴あり」の場合は、「ニュートン多面体の折れ線が$${(1,1)}$$を通る場合を探す」ということと同義になります。
ただそうなる場合もまだたくさんあるんですよね。
頑張って探しましょうか。
作戦としては、穴が何角形かで分けていくのが良いでしょうか。
三次式の場合だと、対称である以上奇数角形なら$${(0,0),(1,1)}$$の線が必要になります。
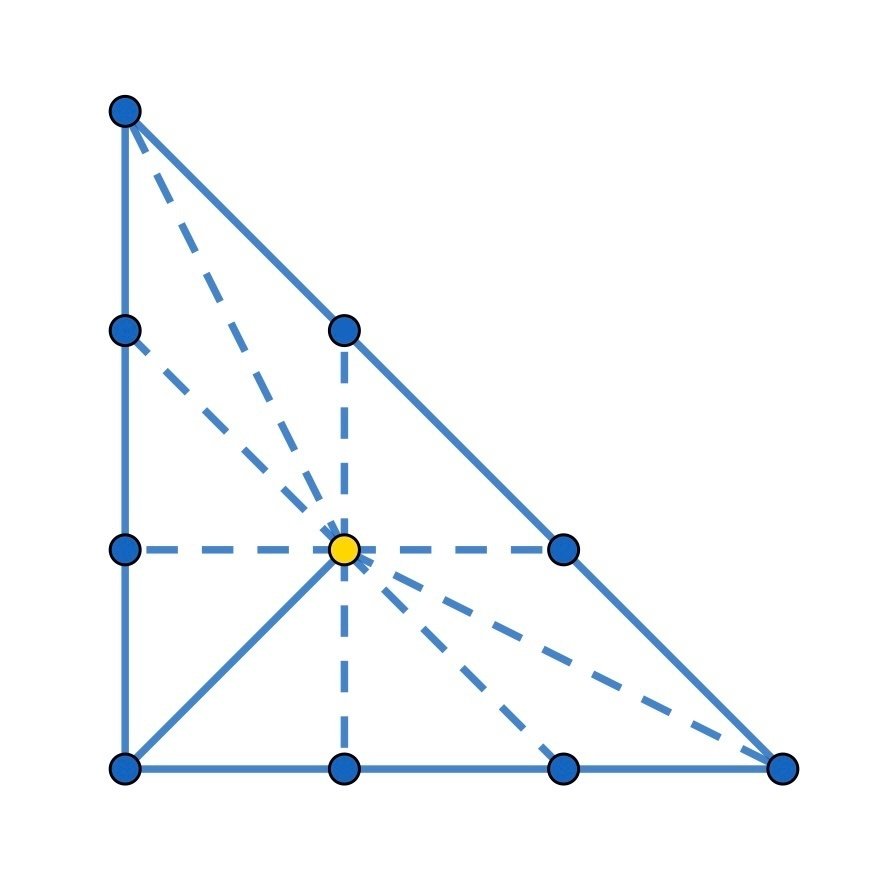
この点線からいくつかを選んで作図することになるのですが、どれも許されるわけではありません。
例えば

こんなふうな取り方をすると、台形ABIJにおいてRからきた線とQからきた線をどう扱うか困ります。
ABIJは台形ですからこの図形から出てくるトロピカルカーブは4本のはずです。しかし、これだと5本になってしまいます。
こういうのを除外しながら数え上げていくと、

多い!
トロピカルカーブ、最初は全部描こうかと思ったんですけど、思ったよりみっちりになりそうなので途中で諦めました。
対称かつ穴ありでこの体たらくですから、すべて数え上げるのはちょっとやりたくないです。
さて、続いては4次式の場合。

かなり点が増えました。
ここまで点が増えるともう少し変なことができます。
たとえば、

こんな図形では
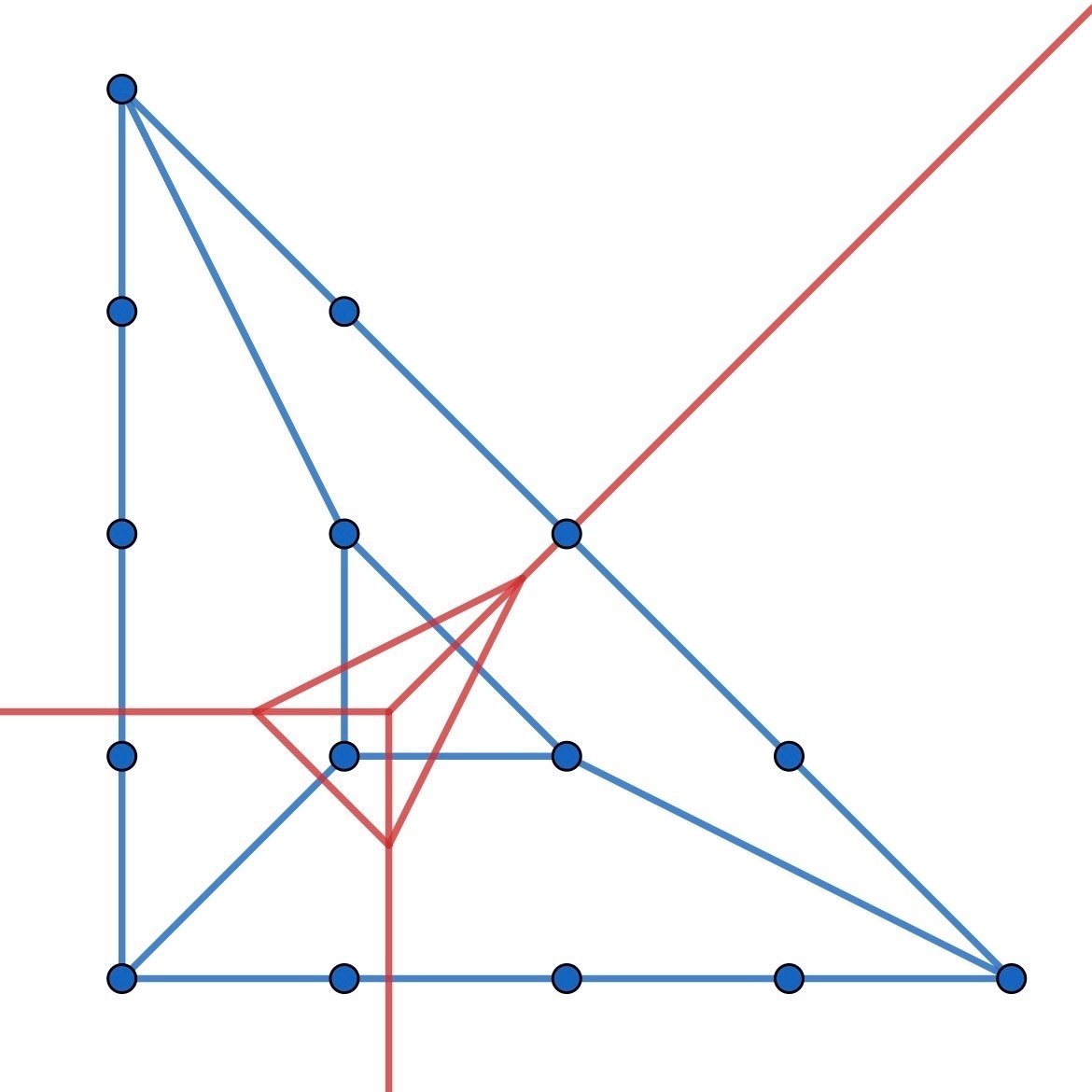
このようなトロピカルカーブが得られます。
ちょうど三次式図形の内部に一次式図形が入れ子にされたようにも見えますね。

この見方は、ちょっと図形の形を変換するともう少し興味深くみてとれます。

さて、この他の話として、負べきも含む多項式も面白いです。$${\pm}$$1次の式は
$$
a_{-1,0}x^{-1}+a_{0,-1}y^-1+a_{0,0}+a_{1,0}x^1+a_{0,1}y
$$
これだと既に$${\pm}$$1次の時点で多角形内に$${(0,0)}$$の頂点をもつので、トロピカルカーブに穴がある場合を考えることができます。

$${\pm}$$2次の場合は頂点が13個になるので、点の数だけでいうと4次式の10点より多いですから、調べ上げるのは一筋縄ではいきません。
仮に(相手が正方形内の分割なので)90度回転の対称性を持つものに限るとすると多少見通しが良く、図形の第一象限はただ対称な2次式のニュートン多角形$${+\alpha}$$の捜索で十分になります。

ただし、$${+\alpha}$$と言っているように、それ以外の場合もあります。
例えば、



このように辺が完全に閉じていない第一象限の図形でも4回対称にコピペすると、ちゃんとした$${\pm2}$$次のニュートン多角形が得られます。
この$${+\alpha}$$の探索も、完全な2次ニュートン多角形からどの辺を切り取ってもOKか考えるとやり易いと思います。
次回はニュートン図形の応用といいますか、通常の多項式とトロピカル多項式のつながりの部分を話そうと思います。
