ファジィ集合のはなし(4)

あいまいなどっちつかずを許してしまうファジィ集合。
前回までは通常の集合(クリスプ集合)にある集合間演算を中心に見ていきました。
ちょっと更新の順序を間違えて、この記事が先に来ちゃってますが、第三回はこちらです。

今回はファジィ特有の部分を見ていこうと思います。

---

言った手前でいきなり但し書きなんですが、ファジィ特有の演算というのはいくらか語弊があるかも知れません。
いくらファジィ特有といっても、メンバーシップ関数の0,1化極限を取ったときに、その演算は普通の集合の既知の演算、または自明な演算になっているべきです。

一方で、ファジィ集合から具体的な値を取り出す操作(クリスプ化、脱ファジィ化)もファジィ特有の演算に含まれるでしょう。

とりあえずまずは前者の方から見ていこうと思います。

---

ファジィ集合の和積演算は前回出てきた和集合(max)、共通部分(min})以外にも、たくさん提案されています。
今回も、特筆しない限りファジィ集合を扱うので、いちいち$${\tilde{}}$$はつけません。
全て心の目で補ってください。

あと、煩雑になりそうなところでは基本的にメンバーシップ関数の変数部分 $${(x)}$$も省略してます。

だって入力が面倒なんだもの。

有名どころを見ていくことにするとして、トップバッターは、

代数和・積

代数和と言っても、「1ぐらいの数」$${+}$$「2ぐらいの数」$${=}$$「3ぐらいの数」というものではありません。
どういうものかというと、こんなものです。

$$
\begin{array}{}A\boxplus B&:&\mu_{A\boxplus B}(x)&=&\mu_A(x)+\mu_B(x)-\mu_A(x)\cdot\mu_B(x)\\A\cdot B&:&\mu_{A\cdot B}(x)&=&\mu_A(x)\cdot\mu_B(x)\end{array}
$$

はじめなのでちゃんと$${(x)}$$つけました。
ここで$${\cdot}$$は普通の積演算です。
これをみて何を思いますかね？

言わずもがな最初に誰しも思うのは、
「なんで$${\cdot}$$なんだよ$${\boxtimes}$$とか$${\boxdot}$$とかでいいじゃん」

じゃないかと思います。
私もそう思いました。
そもそも代数和もフツーに$${+}$$で書く人もいるみたいです。
ちょっとそれだとさすがに紛らわしいというと、$${\dot{+}}$$なんて書き方をする人もいるみたいです。

あとはそうですねぇ、私は普通の集合での要素数演算を思い浮かべました。
もちろんこっちは0から1の値での計算なので、全然別物ではありますが、和で最後積を引くのがなんとも妙ですよね。
ちなみに代数和は英語でProbabilistic sumというようで、代数積はProduct t-normというようです。"代数"どこいった。

実際に演算してみましょう。例によって例の如く、正規分布で0に近い数(青線)と、2に近い数(赤)のメンバーシップ関数を書きます。

このとき代数和は緑の線、代数積は黄色の線になります。

確かに、「0か2に近い数値」と聞かれたら、感覚的には緑の分布になるのかもしれませんし、「0にも2にも近い数字」と問うたら黄色い分布になるような気がします。

さて、見ての通り、代数和積はファジィ和集合・共通部分と似た雰囲気を持っています。
数学で雰囲気とはなんぞやと叱られそうですが、ファジィ和集合・共通部分がmax,minだったことを思い出すと、max,minほど激しい乗り換え(不連続)になるわけではなく、緩やかに両者の関数を繋いでいると言えます。
試しにファジィ和集合・共通部分も書いてみて比較です。

とは言えずの見た目はさして変わりませんね。
赤がmax(ファジィ和集合)、青がmin(ファジィ共通部分)、ピンクが代数和、水色が代数積です。

---

限界和・積

続いては限界和と限界積。なんだこの名前。
英語ではBounded sum,$${\rm{\sout{L}ukasiewicz}}$$ t-normと言います。後者に出てきた$${\rm{\sout{L}ukasiewicz}}$$はポーランドの数学者です。ルーカシェヴィッチと読むようです。(本当は$${\rm{\sout{L}}}$$ではなくスラッシュ付きL, Łなのですが、ちゃんと表示できるか怪しいので代用しています)
boundは境界ですから、まあまあ日本語訳も間違ってなさそうです。
どんな演算かというと、

$$
\begin{array}{}A\oplus B:\mu_{A\oplus B}&=&\min(\mu_A+\mu_B,1)\\A\otimes B:\mu_{A\otimes B}&=&\max(\mu_A+\mu_B-1,0)\end{array}
$$

一見するとなんだこりゃって感じですが、max,minの中に0や1がいるおかげで結果も0から1の間に収まってくれます。
特に限界積は、「はみ出ちゃったから1引いちゃえ」って感じがして、ちょっと愉快にすら感じます。
代数和・積と同じ例でグラフを書いてみましょう。

あれ？　限界積(黄色)どこ……？　ていうか限界和もなんだか代数和とそんなに変わらないような……。

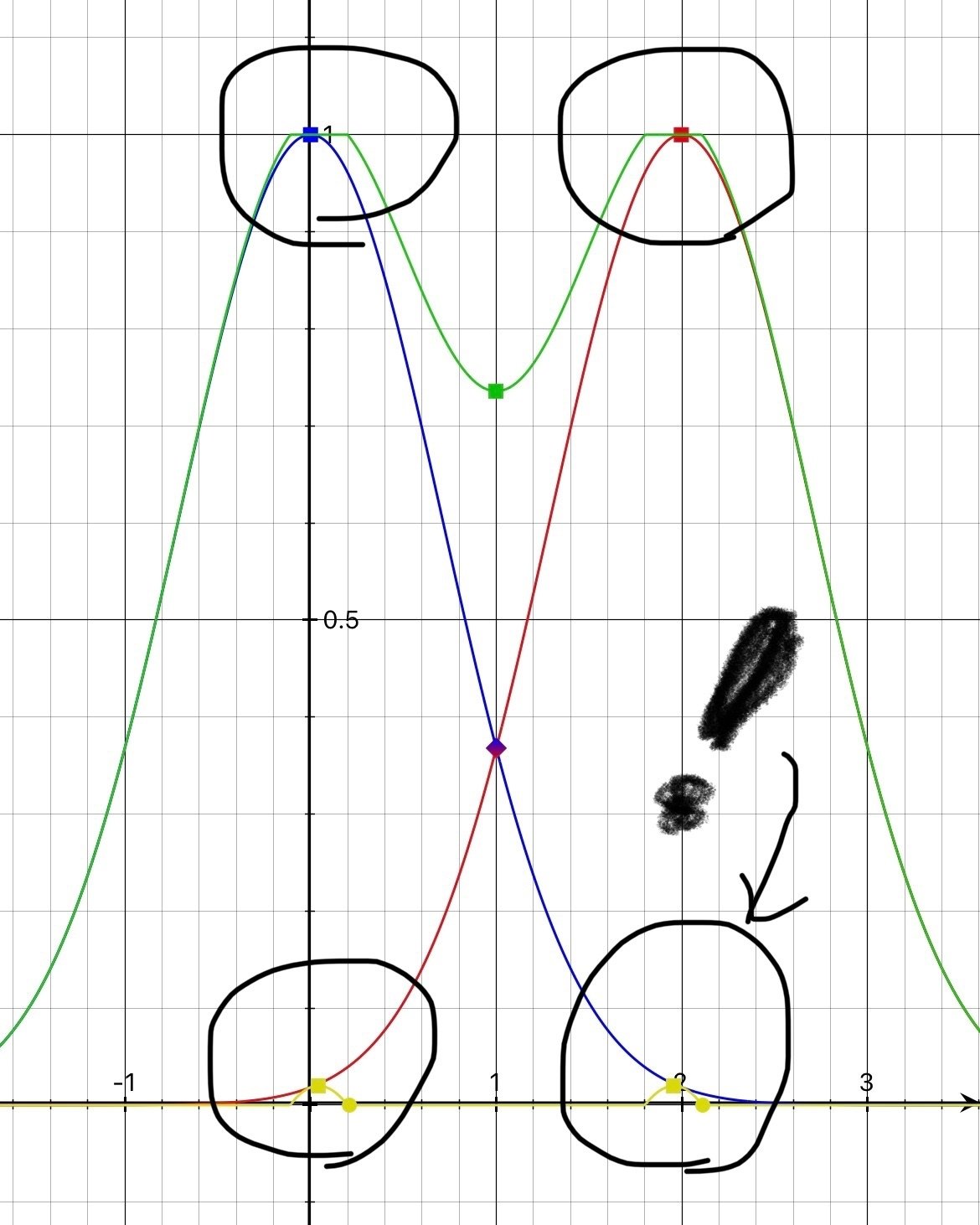
いました。ちいせぇ！

こんな感じである程度メンバーシップ関数が大きいもの同士の和・積でないと結果が潰れてしまいます。

和演算だけ比較してみると、

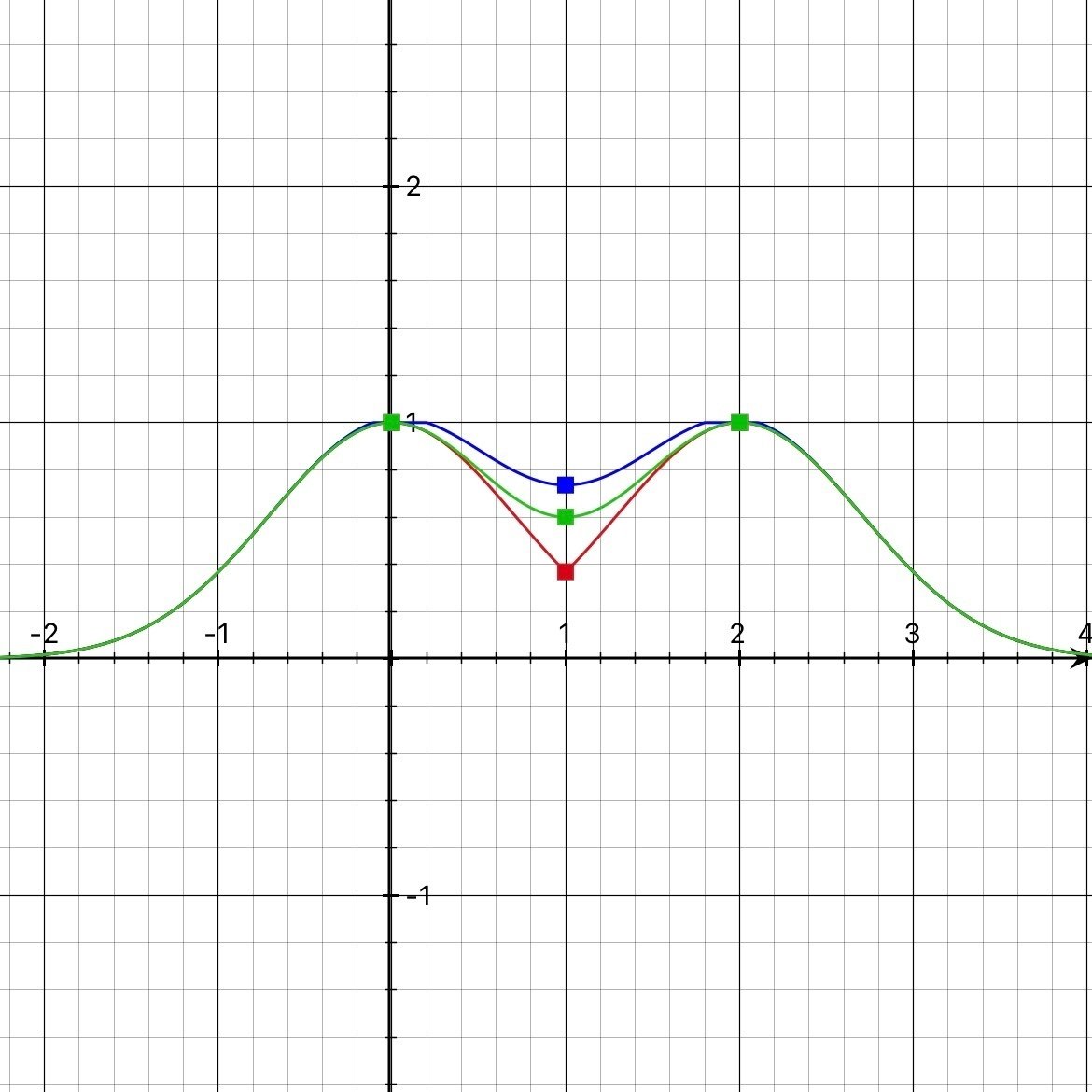
今感じで赤がファジィ和集合、緑が代数和、青が限界和です。
こうしてみると、限界和は確かにリミッター、制限がかかっているようなイメージですね。

---

ここでいうリミッターというのは、ギターなどの音を変えるエフェクターの話をイメージしています。
エフェクターの中にはコンプレッサーという音を圧縮するものがありまして、ベースなんかだととても重宝します。弾いた時の音のばらつきがある程度抑制されるんですね。
このコンプレッサーを目一杯かけて、一切制限した値を越さないようにするエフェクターもありまして、それがリミッターと呼ばれたりします。
つまり、限界和、限界積という用語は、演算結果がしっかり0から1に収まるように、はみ出た部分をちょん切る、制限をつけるという意味で付けられたのかもしれません。

---

激烈和・積

最後は名前からしてすごそうですね。

$$
\begin{array}{}A\dot{\vee}B:\mu_{A\dot{\vee}B}(x)&=&\begin{cases}\mu_A(x)&(\mu_B(x)=0\;なるx)\\\mu_B(x)&(\mu_A(x)=0\;なるx)\\1&(その他)\end{cases}\\\\A\dot{\wedge}B:\mu_{A\dot{\wedge}B}(x)&=&\begin{cases}\mu_A(x)&(\mu_B(x)=1\;なるx)\\\mu_B(x)&(\mu_A(x)=1\;なるx)\\0&(その他)\end{cases}\\\end{array}
$$

こればっかりは定義上$${x}$$を書かないとなんだか気持ち悪いので書いています。

これ、具体例で見てみるとすごいことになります。
まず激烈和、私たちの使っている例だとAもBもメンバーシップ関数は0にならないので、全範囲で結果が1です。

一方激烈積は$${\mu_A(0)=1,\mu_B(2)=1}$$なので、$${x=0,2}$$で激烈積は0以外の値を持ちます。

ということで、ファジィ共通部分、代数積です、限界積、激烈積を並べて書いてみましょう。

うーん、予期してましたが壊滅的に小さいなぁ、見えます？
黄色がファジィ共通部分、水色が代数積、緑が限界積、ピンクが激烈積ですが……。

いました。ちっちゃいと言いますか、もうなんなんでしょうねここまで来ると。

以上の結果からわかるように、こういった和演算、積演算には大小関係があります。

$$
\begin{array}{}
ファジィ和集合(論理和\max)\leq 代数和 \leq 限界和 \leq 激烈和\\\\
激烈積\leq 限界積 \leq 代数積\leq ファジィ共通部分(論理積\min)\end{array}
$$

こんな感じですから、端っこであるところの激烈和・積は確かに激烈と言えるかもしれません。英語でもDrastic t-(co)normというようです。

限界積と代数積の大小関係は以下のように求められます。

$$
\begin{array}{}\mu_{A\cdot B}&=&\mu_A\mu_B\\\mu_{A\otimes B}&=&\max(\mu_A+\mu_B-1,0)\end{array}
$$

ですから、$${\mu_A+\mu_B\leq 1}$$では、

$$
\begin{array}{} &\mu_{A\otimes B}&=&0&\leq&\mu_A\mu_B&=&\mu_{A\cdot B}\\\therefore &\mu_{A\otimes B}&\leq&\mu_{A\cdot B}&\end{array}
$$

一方$${\mu_A+\mu_B >1}$$では、$${\mu_{A\otimes B}=\mu_A+\mu_B-1}$$ですから、

$$
\begin{array}{}0\leq\mu_A+\mu_B-\mu_A\mu_B\leq1\\-1\leq\mu_A+\mu_B-\mu_A\mu_B-1\leq0\\\mu_A+\mu_B-1\leq\mu_A\mu_B\\\mu_{A\otimes B}\leq\mu_{A\cdot B}\end{array}
$$

というふうに言えます。
限界和、代数和の方はすぐ示せると思うんで、あえてやりません。

---

さて、ここまでみてきて、よく読んでる読者なら「なんだそれ」と思う言葉があったかと思います。それも一回でなく何度も出てきている。
そう、t-normです。

t-normは略さず書くと、triangular norm、三角不等式からきている名前です。
こいつ自体は「論理」のほうで出てくるみたいなのですが、論理で出るなら集合でも出るというわけです(雑)。

どんな定義かというと、可換性と結合性、および以下の性質を満たす二項演算$${\top}$$のことを言います。

$$
\begin{array}{}単調性&:&\top(a,c)\leq \top(b,d),&\;(a\leq b,c\leq d)\\単位元が1&:&\top(a,1)=a&\end{array}
$$

これらの規則を満足すればぶっちゃけなんでもいいわけです。
実際t-normの中にはここで紹介しなかった演算積も多々あります。

で、このt-normに双対な演算をt-conormとか、s-normといいます。定義は、

$$
\bot(a,b)=1-\top(1-a,1-b)
$$

こうすることで一般化したド・モルガンの法則も満たされるんですね。

補集合、否定演算を$${a\mapsto1-a}$$としてやります。
ここで、毎回の注意ですが、$${A^c}$$はいわゆる$${\bar{A}}$$、つまり補集合です。
そうすると、

$$
\begin{array}{}a^c\top b^c&=&\top(1-a,1-b)\\(a^c\top b^c)^c&=&1-\top(1-a,1-b)\\&=&\bot(a,b)\\&=&a\bot b\end{array}
$$

というわけで、ド・モルガンの法則が成立しています。

実は今まで見てきた積・和は双対なt-normとt-conormのペアでできています。
だから一見するとなんでこの二つがペアなんだってものがペアになっていたんですね。
例えば代数和は代数積の双対と考えると納得いきます。

$$
\begin{array}{}代数積&=&\mu_A\mu_B\\その双対&:&1-(1-\mu_A)(1-\mu_B)\\&=&\mu_A+\mu_B-\mu_A\mu_B\\&=&代数和\end{array}
$$

---

ときに、ここまできてしまうと、否定演算はそのまま$${a\mapsto 1-a}$$で良いのか、疑問に思うかもしれません。
実のところ否定演算ももう少し詳しく考えられていて、演算の関数$${n(x),(0\leq x\leq1)}$$が$${n(0)=1,n(1)=0}$$を満たせばそれを否定演算、negatorと呼んでしまいます。
ただここまで定義がゆるゆるだと実用的でないのか、以下の二つの性質を持つものが主に扱われます。

・狭義単調減少である(下がり続ける)
・対合である(二回やったら元に戻る)

以上を満たす否定演算をstrongなnegatorというようです。
その中でも代表的なのがよく使う$${a\mapsto 1-a}$$で、こいつはさらに特別で、standard negatorとかcanonical negatorと呼ばれています。
ウッ、カノニカル……。

以上t-norm$${(\top)}$$とt-conorm$${(\bot)}$$, そしてstrongなnegator$${(n)}$$、この三つが有れば一つの演算ペアを作れるので、この三つ組$${(\top,\bot,n)}$$をド・モルガン トリプレット(De Morgan triplet)と呼びます。

つまり、スタンダードなnegator以外でもこういうことを考えられるということになりますね！
いやぁ、否定演算いじりにまで手を出すのはちょっと面倒くさいかなぁ……。

というわけで、裃が面倒臭くなったところで今回も散会といたしましょう。