図形の足し算(ミンコフスキー和)
単発の面白い数学のはなし。
みなさんは小さい頃、図形に図形をぶつけて遊んだことはありますね?
なんのことかって、積み木のことです。
積み木は立体と立体をぶつけてずらして落としてとやっているうちに、「詰めるんだ」と思ってからが楽しくなりますね。
みなさんも一歳くらいの時そうだったでしょ?
あるいは敷き詰めるパズルとか、学校で三角定規を使うようになって遊んだりとか、物と物をすり合わせて動かすってことは、算数や数学を意識しなくとも人間、一度はやったことがあるかと思います。
この時にふと、
「二つの定規を離さず、すり合わせて描けるところ(領域)ってどんな形になるんだろう」
と、思ったことがあれば、あなたは数学者の素質があると思います。物理屋の裃が言うんだからあんまりあてにしないでください。
冗談はさておき、中学受験なんかでもこの手の図形の問題は頻出だったりします。

こういうやつね。
どこの塾でもきっと言っていると思いますが、要するにル○バです。
この円を滑らないよう四角の周りに転がしていくと、

こうなります。
で、今回はこの問題の話をしたいのではありません。
こんなかんじの図形の足し算引き算を考えたいのです。
実は多少上の例とは違うんですが、既にちゃんと数学ではこういう和も研究されてまして、今日はそのミンコフスキー和というものを考えます。
このミンコフスキー、Minkowskiと書きます。
物理ではあのミンコフスキー空間で有名なミンコフスキーです。
フルネームだとヘルマン・ミンコフスキー(Hermann Minkowski)。
実は彼の兄オスカー・ミンコフスキー(Oskar Minkowski)は生理学者で、オスカーの息子ルドルフ・ミンコフスキー(Rudolph Minkowski)は天体物理学者です。
なんかすごい家系だな。
もちろんベルヌーイ家ほどではありませんが。
ミンコフスキー和は以下のように定義されます。
空間上の領域$${A,B}$$に対して、
$$
A+_mB=\{{\bf a}+{\bf b}|{\bf a}\in A,{\bf b}\in B\}
$$
つまり、位置ベクトルを各々足して、その先端の塗りつぶす領域をまとめるとミンコフスキー和になるのです。
一応ここでは普通の数の和$${+}$$との混同を避けるべく$${+_m}$$と書いていますが、そんなこといちいち気にせず普通に$${A+B}$$と書くことが多そうです。
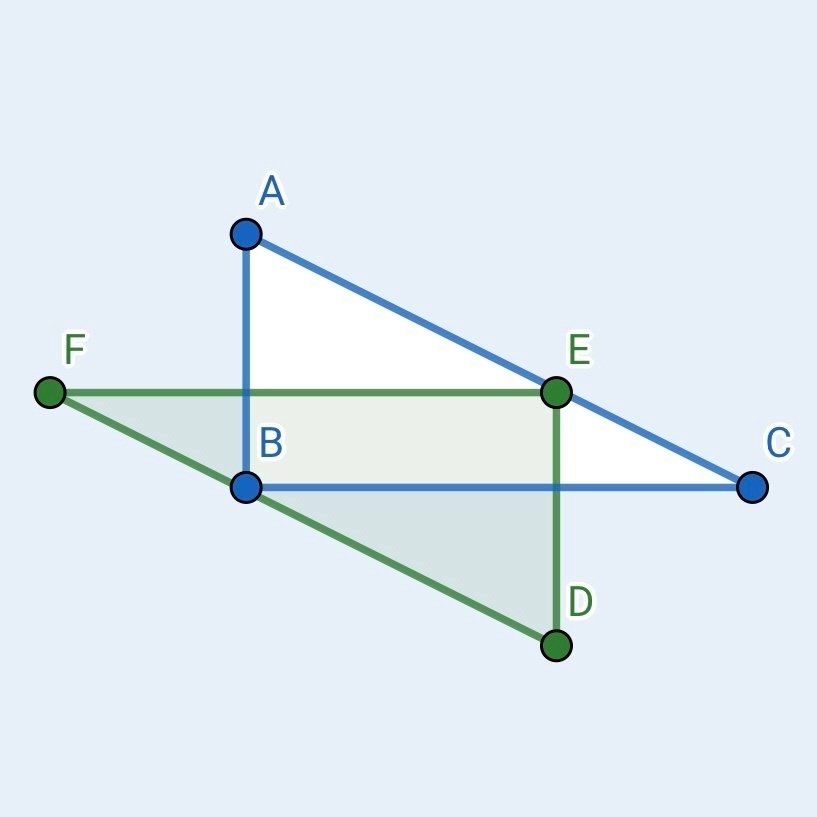
具体的にどんなことをするのか、簡単な例でやってみます。

この二つの三角形を足してやります。
まず青をベースにして緑をミンコフスキー和します。

こんな感じで、やりたいことは結局「図形のすり合わせ」です。
もっと細かく三角形をずらして書けば、

となります。
この黄色の領域がミンコフスキー和の結果です。
では緑をベースにするとどうなるでしょう。
そもそもベクトルの和が可換ですから、ミンコフスキー和も可換のはずです。

このようになります。
ここで注意しなくてはいけないのが、あくまで図形の基準点を沿わせるということです。
今の場合ですと青の三角形のBを緑の三角形DEFに沿って動かしています。
つまり

こういう位置に青の三角形が来ることはありません。
これが上でウニャウニャ「多少問題とは違うんだけど」と言っていたゆえんです。
最初に挙げたル◯バ問題はまわりをぐるりと一周するので、ここで出てきたミンコフスキー和ではNGという位置も含んでいるのです。
NGな位置を含むのにはどうするか、それを考えるのは後にして、ミンコフスキー和には差もちゃんとありますので先にそっちをみておきます。
ミンコフスキー和に対する差の演算はどうなるのか。
見た目としては上の図でいう黄色から青を引いたら緑ということなのですが、意外にもこれがイメージしにくいんです。
こんなことをします。
$$
A -_m B=(A^c+_m(-B))^c
$$
なんだこれ?
ここで出てくる$${A^c}$$は$${A}$$の補集合を意味します。つまり$${\bar{A}}$$と同じ意味です。
まあ試しにやってみましょう。

図の赤の部分が黄色(A)の補集合です。
ここから元の図で言うところの三角形ABCを引きます。
引く方の集合は$${-B}$$と書かれています。
これは集合の元、位置ベクトルを全部$${-1}$$倍するということなので、

図の青い三角形を用意します。
あとはこれを赤の淵にそって移動させます。

この時、通った部分は$${A^c+(-B)}$$になります。

図では黒く塗りました。
あとは黒のの補集合をとるので、確かにこれは緑の三角形DEFに一致します。
さて、以上をふまえて最初の問題とミンコフスキー和の相違点を克服します。
まず、いわゆるル◯バ問題で二つの三角形を合成すると以下のような図形が得られます。

ここで受験算数に慣れていると、転がり問題じゃないの? と思うかもしれませんが、転がり問題をミンコフスキー和です考えるのはかなり面倒(図形の外周や角度にもよる)ですし、最大範囲は図形内最長距離での円弧の包絡線ですからあまり面白くない。
そこで平行移動の問題にしておきます。
転がり問題への拡張は気が向いたら考えます。
このオレンジの図形に対し、三角形DEFのミンコフスキー差をとります。$${\triangle DEF}$$に対し、$${- \triangle DEF}$$として紫の三角形PILを用意します。

そうすると赤の部分が残ります。
こいつの正体がわかれば、ル◯バ問題の演算が何になっているか分かりそうです。
で、こいつ、よくみるとわかりますが、

こんなふうに、青の三角形と紫の三角形のミンコフスキー和になっています。
つまりル◯バ問題演算(ここでは$${+_l}$$と書くことにします)は、図形A,Bに対し、$${A+_lB=A+_m(-B)+_mB}$$をしたものということになります。
またこの例からもわかるように、$${B+_m(-B)\neq B-_mB}$$です。
で、さらに厄介なことに、つまりル◯バ演算は非可換です。
いま、$${A=\triangle ABC(青),B=\triangle DEF(緑)}$$とします。

このとき、上の黄色が$${B+_lA=B+_m(-A)+_mA}$$で、下の青紫が$${A+_lB=A+_m(-B)+_mB}$$です。
それぞれオレンジが$${B+_m(-A)}$$, 藤色が$${A+_m(-B)}$$となっています。
これをみる限りだと$${A+_lB}$$と$${B+_lA}$$は点対称にみえますが、一般には成り立ちません。
これは余談なんですけど、$${A+_m(-B)}$$のことをミンコフスキー差と呼ぶ人もいるみたいです。
念のため、文献を読むときは注意がいるかと思います。
さて、ル◯バ問題はさておいて、もう少しミンコフスキー和差を掘っていきましょう。
実はミンコフスキー差を定義する時、未定義な演算をいくつかやってしまっています。
またミンコフスキー和の単位元もちゃんと調べていません。
というわけでまずミンコフスキー和の単位元を探しましょう。
これはそんな難しい話ではなく、動かさないなら集合としては空集合、図形であれば全くの無か、あるいは点そのもの(零ベクトル)ではないかと予想できます。
実際この予想は正しくて、ミンコフスキー和の単位元は零ベクトル$${{\bf 0},\{0\}}$$です。
それもそのはずで、零ベクトルは
$$
{\bf a}+{\bf 0}={\bf a}
$$
ですから、ミンコフスキー和の定義からして
$$
A+_m{\bf 0}=A
$$
つまりミンコフスキー和の単位元と言えるわけです。
次の問題点。
ミンコフスキー差の時に、未定義の演算を導入している点について。
ミンコフスキー差は
$$
A-_mB=(A^c+(-B))^c
$$
と定義しましたが、これ、まず$${-B}$$が何なのかちゃんと考えた方が良さそうです。
それともちろん、補集合$${A^c}$$も怪しいです。というのも、僕らは図形を例にしているのであって、いきなり集合を引っ張り出すのはいささか飛躍だと思います。
まず図形と集合のあたりから補足していきます。
ミンコフスキー和差の元は図形をベクトルの集合と捉えるのですから、図形を$${X}$$その内部に座標点$${P}$$があるとき$${P\in X}$$と書くことにして、
$$
\begin{array}{}A_X&=&\{{\bf a}\;|\;{\bf a}=\vec{OP},P\in X\}\\&=&\{{\bf a}\;|\;{\bf a}\in X\}\end{array}
$$
こうして定めた$${A_X}$$は図形$${X}$$に対するミンコフスキー和の元と言えそうです。
二段目の式は「そんな細かく言わなくて良くね?」という私の気持ちです。
以上を踏まえて、$${-B}$$です。
これはベクトルのスカラー倍同様、図形のスカラー倍を定義するのが良いかと思います。
すなわちある図形Aに対して
$$
kA=\{k{\bf a}\;|\;{\bf a}\in A,k\in {\mathbb R}\}
$$
こうすれば
$$
-A=\{-{\bf a}\;|\;{\bf a}\in A\}
$$
ですから、ちゃんと目論み通り原点対称な図形が得られるとわかります。
また、$${k=0}$$なら零ベクトルのことになり、
$$
{\bf 0}=\{0\}
$$
なんだろう……うーん、書いてみたもののあまり意味はないですね。
最後に補集合ですが、これはちょっとおもしろい。
なぜって普通の集合は境界をもっています。
境界のある集合の補集合は境界のないですから、僕らが今からやる図形の補集合演算は僕らのイメージする図形とはだいぶ様子が異なります。
実際上の例では明らかに赤い部分、すなわち$${A^c}$$が画面に収まりきっていません。
それもそのはずです。無限遠もぜーんぶ含むんですから。
書くとするとこういうことでしょうか、
$$
A^c=\{{\bf a}\;|\;{\bf a}\notin A\}
$$
こうしておけばひとまず$${(A^c)^c=A}$$なんてのも合点がいくような気がします。
さて、ミンコフスキー差をつくる演算が出揃ったので、改めてミンコフスキー差を掘ります。
まず以下の演算を考えます。
$$
\begin{array}{}(A^c+(-A))^c\end{array}
$$
これ、どんな結果になるのでしょう。
試しに図で書いてみると、こうなります。
三角形ABCを図形A,三角形DEFを図形$${-A}$$として、基準点Eを動かしている最中をイメージしてます。
このままEをAC上でスライドさせるのですから、ここまで、つまり$${A^c+(-A)}$$は「全領域」といえ……、いや、ちょっとこれは怖い。
と言いますのも、$${A^c}$$は辺を持ちません。
ギリギリ辺の外側からしか領域にならない。
ということは、ギリギリで原点(上の図だとB)は通らないと言えます。
つまり、$${A^c+_m(-A)}$$は「原点以外の全領域」です。
これなら最終結果$${(A^c+_m(-A))^c}$$は原点、すなわち$${\bf 0}$$といえそうです。
$$
A-_mA=(A^c+_m(-A))^c={\bf 0}
$$
この意味でも零ベクトルがミンコフスキー和の単位元といえそうです。
一方全くの無、空集合$${\emptyset}$$もミンコフスキー和で重要な役割を持ちます。
空集合を演算すると、以下のようになるそうです。
$$
A+_m\emptyset=\emptyset
$$
なんと、和則において吸収元(掛け算における0)の役割をします。
これ、どうしてそうなるのかずいぶん悩みました。
今の所の自分は
・$${\emptyset}$$は領域$${{\mathbb R}^2}$$の全ての対象(ベクトル)を含んでいない。
・もし図形Aに$${\emptyset}$$を加えると、その結果は今注目している全ての対象の外にはみ出てしまう。
・ということは結果もやっぱり要素を持てず$${\emptyset}$$だと言わざるを得ない。
・よって$${A+_m\emptyset=\emptyset}$$
と解釈して、疑問の龍虎を抑え込んでいます。
さて、以上こうしてみてきたミンコフスキー和と差ですが、重要なことを後回しにしてました。
本当にどんな図形でもミンコフスキー和と差は定義できるのか?
これ、答えを言うとNoです。
実は差がうまくいかないことがあります。
図形が凸でないと、差でもとに戻れないことがあります。

図の青い五角形はBで凹んでいるので凸ではありません。
これに緑の三角形をミンコフスキー和で加えると黄色い図形になります。
黄色の図形から緑の三角形をミンコフスキー差で引くには、赤い三角形をスライドして考えていきますが、見ての通り点Pに点Rが重なるとき、三角形RSBに相当する部分を引き損ねてしまいます。
そういうわけで、ミンコフスキー差まで考えると凸な図形を前提におくべきでしょう。
ミンコフスキー和であと気になるのは面積の扱いですが、ちょっとこれは一般の図形で考えるのは面倒そうです。
格子点に頂点を持つような多角形ならまだいろいろ話せることがありそうですが、ひとまずミンコフスキー和差の紹介はここまでとします。
みなさんもぜひ童心にかえって図形と図形を擦り合わせて遊んでみてください。
